非定数のバックグラウンドを持つフィット関数

内容

1 サマリー
2 学習する項目
3 サンプルとステップ

サマリー

Originの組み込み関数の多くは、次のように定義されます。

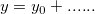
$\begin{matrix}y=y_0+......\end{matrix}$

ここでy0は、定数のバックグラウンドとして扱うことができます。では、非定数のバックグラウンドを持つ曲線は、どのようにフィットしたら良いでしょうか?1つの方法として、OriginProで提供しているピークアナライザを使うことができます。ピークアナライザには、指数または多項式のバックグラウンドを含む基線を減算する方法がいくつかあります。このチュートリアルでは、ピークアナライザを使わずに、このような曲線をフィットする方法を示します。

必要なOriginのバージョン:8.0 SR6

学習する項目

ワークシートクエリの復習
nlfxFuncName メソッドで組み込み関数を引用する
パラメータの自動初期化

サンプルとステップ

データを準備する

\Samples\Spectroscopy\Peaks on Exponential Baseline.datをインポートして、このチュートリアルを開始します。ワークシートのスパークラインから、曲線に2つのピークがあることが分かります。問題を単純化するため、この例の1つのピークをフィットします。

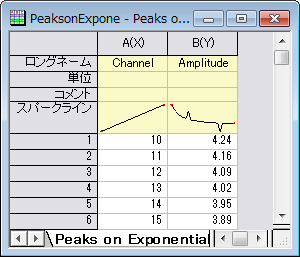
Image:Fit_Function_with_Nonconstant_Background_001.png

メニューからワークシート：ワークシートクエリと操作して、ワークシートクエリダイアログを開きます。行1から行240のデータを抽出します。

Image:Fit_Function_with_Nonconstant_Background_002.png

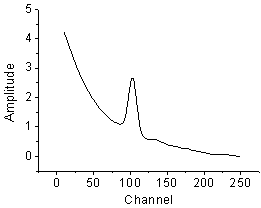
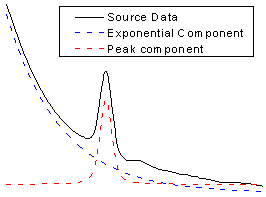
フィットする曲線は次のようになります。

Image:Fit_Function_with_Nonconstant_Background_003.png

関数を定義する

下の図から分かるように、元の曲線は指数関数形崩壊（バックグラウンドに相当）とVoigtピークの組み合わせである事が分かります。

Image:Fit_Function_with_Nonconstant_Background_004.png

関数全部を記述して関数を定義しなければならないでしょうか?例えば：

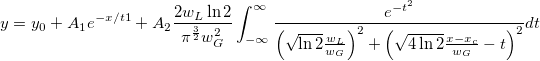
$y=y_0+A_1e^{-x/t1}+A_2\frac{2w_L\ln{2}}{\pi^{\frac{3}{2}}w^2_G}\int_{-\infty}^{\infty}\frac{e^{-t^2}}{\left( \sqrt{\ln2}\frac{w_L}{w_G} \right)^2 + \left( \sqrt{4\ln{2}}\frac{x-x_c}{w_G}-t \right)^2}dt$

これは複雑な数式で、無限区間の積分も含まれています。数式を直接記述するのは大変です。Originには次の2つの組み込み関数があります。

ExpDec1

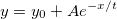
$\begin{matrix}y=y_0+Ae^{-x/t}\end{matrix}$

Voigt

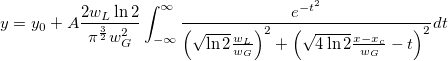
$y=y_0+A\frac{2w_L\ln{2}}{\pi^{\frac{3}{2}}w^2_G}\int_{-\infty}^{\infty}\frac{e^{-t^2}}{\left( \sqrt{\ln2}\frac{w_L}{w_G} \right)^2 + \left( \sqrt{4\ln{2}}\frac{x-x_c}{w_G}-t \right)^2}dt$

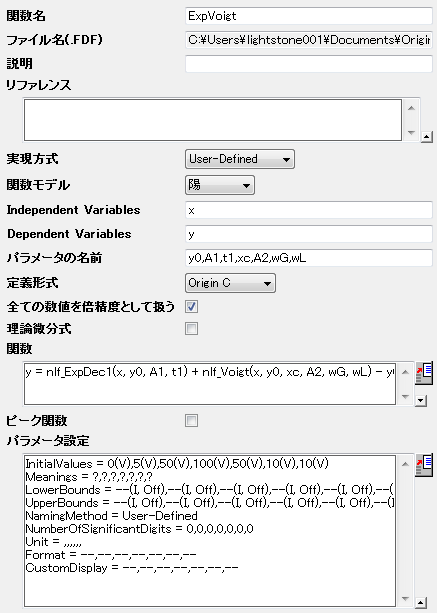
nlfxFuncName メソッドを使って、これら2つの関数を引用し、新しい関数を簡単に作成することができます。F9を押し、フィット関数オーガナイザを開き、以下のように関数を定義します。


関数名：	ExpVoigt
実現方式：	ユーザ定義
独立変数：	x
従属変数：	y
パラメータの名前：	y0, A1, t1, xc, A2, wG, wL
定義形式：	Origin C
関数：	y = nlf_ExpDec1(x, y0, A1, t1) + nlf_Voigt(x, y0, xc, A2, wG, wL) - y0;

Note:

組み込み関数名のいくつかは、実際のDLL関数名と一致しません。Voigt5.FDFで定義しているVoigt関数のように、メモ帳でFDFファイルを開く場合、 [GENERAL INFORMATION]セクションの中に次の行があります。

Function Source=fgroup.Voigt5

"fgroup"の後の名前は、nlfxFuncNameに入れる実際の名前です。
Origin 8.1 SR2以前のバージョンでは、関数のボディは次に定義されるような旧式のnlfxFuncNameを使ってください。
```
y = nlfxExpDec1(x, y0, A1, t1) + nlfxVoigt(x, y0, xc, A2, wG, wL) - y0;
x; xc; A1; t1; A2; wG; wL;
```
最後にパラメータを一覧にするのは、関数でこれらのパラメータを使っているにもかかわらず、関数内でパラメータが使われていないというエラーを避けるためです。これを入れないと、関数のコンパイルがうまくいきません。

パラメータ設定の右にあるボタンをクリックし、これらのパラメータの初期値を入力します。


y0:	0
A1:	5
t1:	50
xc:	100
A2:	50
wG:	10
wL:	10

ですので、最終的な定義部分は、次のようになります。

Image:Fit_Function_with_Nonconstant_Background_006.png

自動パラメータ初期化

上記のセクションで、パラメータの初期値を固定にセットしました。有力なフィット結果を知っていれば、このように初期値をセットすることができます。しかし、データが変わった場合はどうでしょうか?Originは、初期値を推定するOrigin Cインターフェースを提供しています。パラメータ初期化コードを使うには、パラメータの自動初期化を行うとOrigin Cを使用するチェックボックスにチェックを付け、アイコンをクリックしてコードビルダでコードを編集します。
(初期値をよく分かっていたり、コードを記述したくない場合、このセクションを読み飛ばしても構いません。)

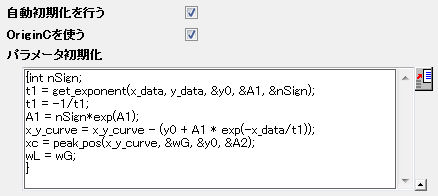
Image:Fit_Function_with_Nonconstant_Background_007.png

曲線は2つのコンポーネントで構成され、これら2つの部分を分けることで、パラメータ値を推測できます。初期化コードには次を含みます。

get_exponent関数を使って、曲線をフィットし、指数成分に対するパラメータ値を取得します。
元のデータからバックグラウンド(指数成分)を除去します。
peak_pos 関数を使って、ガウスピークによってピークを近づけ、ピークコンポーネントに対する初期値をセットします。

コードビルダ内の初期化コードは次のようになります。

void _nlsfParamExpVoigt(
// フィットパラメータ:
double& y0, double& A1, double& t1, double& xc, double& A2, double& wG, double& wL,
// 独立データセット
vector& x_data,
// 従属データセット
vector& y_data,
// 曲線
Curve x_y_curve,
// 補助的なエラーコード
int& nErr)
{
        // 編集可能部分の開始
        int nSign;
        //  y = y0+A*exp(R*x)に対するパラメータの値y0, ln(A), Rを評価
        t1 = get_exponent(x_data, y_data, &y0, &A1, &nSign);
        // フィット関数に対する指数成分の値をセット
        t1 = -1/t1;
        A1 = nSign*exp(A1);
        // 曲線から指数成分を除去
        x_y_curve = x_y_curve - (y0 + A1 * exp(-x_data/t1));
        // フィットしてピーク値を取得
        xc = peak_pos(x_y_curve, &wG, &y0, &A2);
        wL = wG;
        // 編集可能部分の終了
}

Note:

自動初期化を行うにチェックを付けて、初期化コードを入力すると、これらのコードはパラメータ設定での初期値にも影響します。

曲線をフィットする

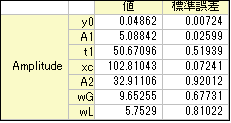
使用したパラメータ初期化の方法に関係なく、列Bを選択し、Ctrl + Yを押して、NLFitダイアログを開き、ExpVoigt関数を選んでフィットします。結果は次のようになります。

Image:Fit_Function_with_Nonconstant_Background_008.png

Skip Navigation Links

English | Deutsch | 日本語