Anpassungsfunktion mit nicht-konstantem Hintergrund
Zusammenfassung
Viele Standardfunktionen von Origin werden definiert mit:
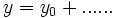
, wobei y0 als der "konstante Hintergrund" betrachtet werden
kann. Wie ist es möglich, Kurven mit nicht-konstantem Hintergrund anzupassen?
Eine Möglichkeit besteht in der Verwendung des Impulsanalysators. Der
Impulsanalysator bietet mehrere Methoden, um die Basislinie zu subtrahieren,
einschließlich des exponentiellen oder polynomialen Hintergrunds. In diesem
Tutorial zeigen wir Ihnen, wie Sie so eine Kurve mit Hilfe des Impulsanalysators
anpassen können.
Origin-Version mind. erforderlich: 8.0 SR6
Was Sie lernen werden
Beispiel und Schritte
Vorbereiten der Daten
Beginnen Sie dieses Tutorial durch den Import der Datei \Samples\Spectroscopy\Peaks
on Exponential Baseline.dat. Die Sparkline des Arbeitsblatts zeigt
uns, dass es in der Kurve zwei Peaks gibt. Um das Problem zu vereinfachen,
passen wir in diesem Beispiel nur einen Peak an.
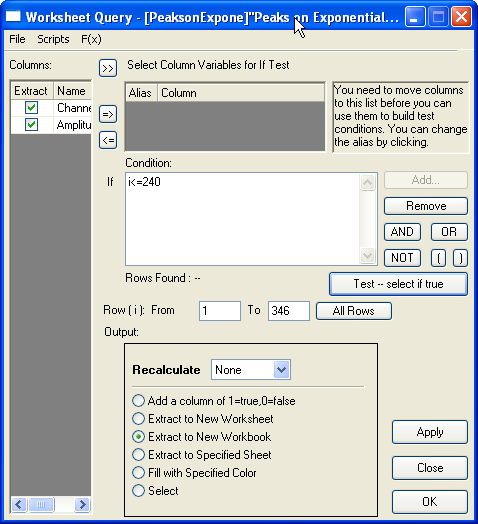
Rufen Sie jetzt das Dialogfeld Arbeitsblattanfrage über Worksheet :
Arbeitsblattanfrage auf. Extrahieren Sie die Daten von Zeile 1 bis
Zeile 240:
Die anzupassende Kurve sollte folgendermaßen aussehen:
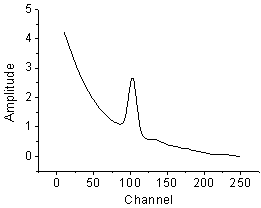
Definieren der Funktion
Wie unten dargestellt, betrachten wir die Quellkurve als die Kombination
einer exponentiellen Zerfallskomponente (der Hintergrund) und einem Voigt-Peak:
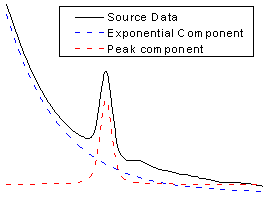
Soll die gesamte Gleichung aufgeschrieben werden, um die Funktion zu
definieren, sähe das folgendermaßen aus:
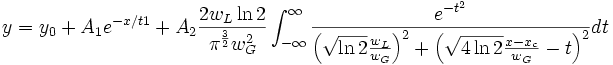
Es handelt sich hierbei um eine komplizierte Gleichung, die eine unendliche
Integration enthält. Das Aufschreiben einer solchen Gleichung ist mühsam.
Wir haben allerdings bereits diese zwei Standardfunktionen:
ExpDec1:
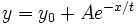
Voigt:
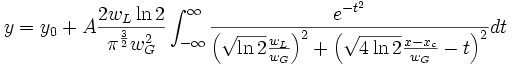
Daher können wir einfach die Methode nlfxFuncName verwenden,
um diese zwei Standardfunktionen anzugeben und eine neue Funktion zu erstellen.
Drücken Sie F9, um den Dialog Fitfunktionen verwalten zu
öffnen und unten eine Funktion zu definieren:
|
|
|
|---|
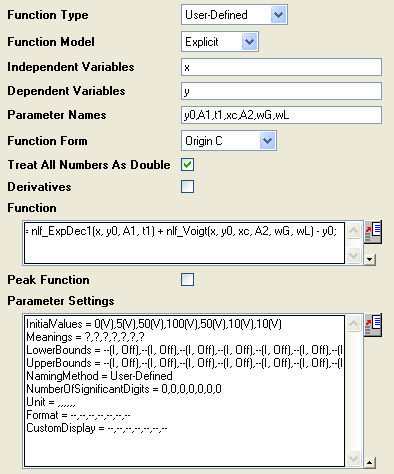
| Funktionsname: |
ExpVoigt |
| Funktionstyp: |
Benutzerdefiniert |
| Unabhängige Variable: |
x |
| Abhängige Variable: |
y |
| Parameternamen: |
y0, A1, t1, xc, A2, wG, wL |
| Funktionsform: |
Origin C |
| Funktion: |
y = nlf_ExpDec1(x, y0, A1, t1) + nlf_Voigt(x, y0, xc, A2, wG, wL) -
y0; |
Hinweis:
-
Einige der Standardfunktionsnamen sind nicht konsistent mit dem tatsächlichen
Namen der DLL-Funktion. Wie die Voigt-Funktion ist dies in Voigt5.FDF
definiert. Wenn Sie die FDF-Datei mit Notepad öffnen, können Sie eine
Zeile im Abschnitt [GENERAL INFORMATION] (Allgemeine Informationen) sehen,
die besagt:
- Function Source=fgroup.Voigt5
Der Name nach "fgroup" ist der tatsächliche Name, der in
nlf_FuncName eingegeben werden sollte.
-
In Versionen vor Origin
8.1 SR2 sollte der Funktionskörper die alte Notation nlfxFuncName
verwenden und definiert werden durch:
y = nlfxExpDec1(x, y0, A1, t1) + nlfxVoigt(;x, y0, xc, A2, wG, wL) - y0;
x; xc; A1; t1; A2; wG; wL;
Die Parameter werden am Ende aufgelistet, um zu vermeiden, dass der
Fehler "parameter not used inside the function body" (Parameter
werden in dem Funktionskörper nicht verwendet) auftritt, obwohl Sie diese
Parameter bereits verwenden. Falls nicht, können Sie die Funktion nicht
erfolgreich kompilieren.
|
Klicken Sie auf die Schaltfläche  rechts von den Parametereinstellungen und geben Sie diese
Parameterinitialisierungswerte ein: rechts von den Parametereinstellungen und geben Sie diese
Parameterinitialisierungswerte ein:
|
|
|
|---|
| Y0 |
0 |
| A1 |
5 |
| t1: |
50 |
| xc: |
100 |
| A2 |
50 |
| wG: |
10 |
| wL: |
10 |
Der endgültige Teil der Funktionsdefinition sollte folgendermaßen aussehen:
Automatische Parameterinitialisierung
Im obenstehenden Abschnitt wurden die festen Parameterinitialisierungswerte
gesetzt. Wenn die die möglichen Anpassungsergebnisse kennen, können Sie
die Initialisierungswerte dementsprechend festlegen. Aber was passiert,
wenn sich die Daten ändern? Origin bietet eine Origin C-Schnittstelle
zum "groben Schätzen" der Initialisierungswerte. Um den Parameterinitialisierungscode
zu verwenden, stellen Sie sicher, dass die Kontrollkästchen Automatische
Initialisierung aktivieren und Origin C verwenden aktiviert
sind, und bearbeiten Sie den Code im Code Builder, indem Sie auf das Symbol
 klicken. klicken.
(P.S: Sollten Sie die Initialisierungswerte gut kennen oder Codierung nicht
mögen, überspringen Sie bitte diesen Abschnitt.)
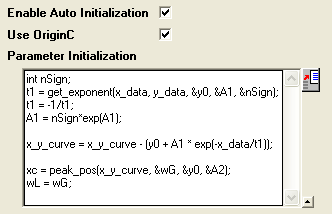
Jetzt, da die Kurve sich aus zwei Komponenten zusammensetzt, können
wir die Parameterwerte grob schätzen, indem diese zwei Teile getrennt
werden. Der Initialisierungscode beinhaltet dann Folgendes:
- Verwenden Sie die Funktion get_exponent zum Anpassen der Kurve und erhalten Sie
auf diese Weise die Parameterwerte für die exponentielle Komponente.
- Entfernen Sie den Hintergrund -- exponentielle Komponente -- aus
den Quelldaten.
- Führen Sie eine Annäherung an den Impuls durch den Gauss-Impuls
mit Hilfe der Funktion peak_pos durch und legen Sie die Initialisierungswerte
für die Impulskomponente fest.
Der Initialisierungscode im Code Builder sollte folgendermaßen aussehen:
void _nlsfParamExpVoigt(
// Fit Parameter(s):
double& y0, double& A1, double& t1, double& xc, double& A2, double& wG, double& wL,
// Independent Dataset(s):
vector& x_data,
// Dependent Dataset(s):
vector& y_data,
// Curve(s):
Curve x_y_curve,
// Auxilary error code:
int& nErr)
{
// Beginning of editable part
int nSign;
// Evaluates the parameters' value, y0, ln(A) and R for y = y0+A*exp(R*x).
t1 = get_exponent(x_data, y_data, &y0, &A1, &nSign);
// Set the exponential component values for the fitting function.
t1 = -1/t1;
A1 = nSign*exp(A1);
// Remove the exponential component from the curve;
x_y_curve = x_y_curve - (y0 + A1 * exp(-x_data/t1));
// Fit to get peak values.
xc = peak_pos(x_y_curve, &wG, &y0, &A2);
wL = wG;
// End of editable part
}
| Hinweis:
Wenn Sie Automatische Initialisierung aktivieren aktivieren und
den Initialisierungscode eingeben, deckt sich dieser Code mit den Initialisierungswerten
in Parametereinstellungen. |
Anpassen der Kurve
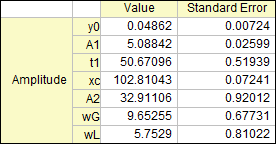
Unabhängig davon, welche Parameterinitialisierungsmethode Sie verwenden,
markieren Sie Spalte B und drücken Sie Strg + Y, um das Dialogfeld
NLFit aufzurufen. Wählen Sie dann die Funktion ExpVoigt und führen Sie
die Anpassung durch. Das Ergebnis sollte folgendermaßen aussehen:
|