4.2.2.19 Quoting Built-in Functions in Your New FunctionUDF-Quote-BuiltInFunc
Summary
This tutorial will show you how to reference a built-in function when creating a user-defined fitting function.
Minimum Origin Version Required: Origin 8.0 SR6
What you will learn
This tutorial will show you how to:
- Define a piecewise fitting function
- Access built-in functions in you new function
- Auto initialize the parameters
Steps
Data
Start by importing the file \Samples\Curve Fitting\Asymmetric Gaussian.dat into a new workbook.
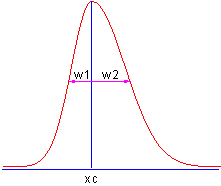
Highlight column B and create a graph. The peak in the data is slightly skewed to the right. How to fit such a curve? One idea is to divide the curve into two parts - We can consider this curve to be composed of two Gaussian function as below. These two Gaussian curves share the same baseline and peak center, but differ in peak width and amplitude.
Define the Function
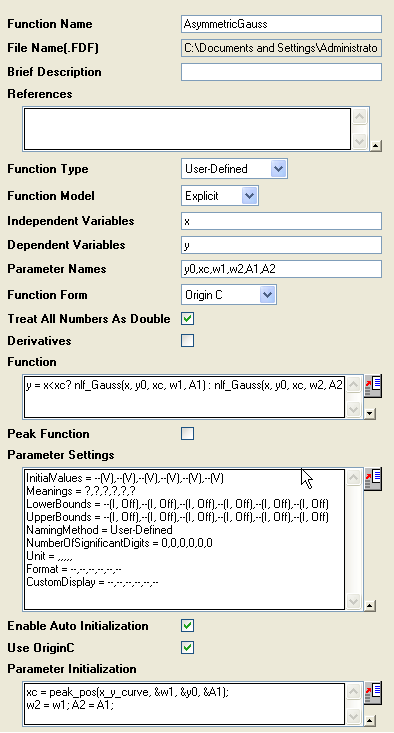
Press F9 to open the Fitting Function Organizer and define the function as below:
| Function Name:
|
AsymmetricGauss
|
| Function Type:
|
User-Defined
|
| Independent Variables:
|
x
|
| Dependent Variables:
|
y
|
| Parameter Names:
|
y0, xc, w1, w2, A1, A2
|
| Function Form:
|
Origin C
|
| Function:
|
y = x<xc? nlf_Gauss(x, y0, xc, w1, A1) : nlf_Gauss(x, y0, xc, w2, A2);
|
| Note:
For versions before Origin 8.1, the function body should be defined as:
y = x<xc? nlfxGauss(x, y0, xc, w1, A1) : nlfxGauss(x, y0, xc, w2, A2);
x; y0; xc; w1; w2; A1; A2;
Listing the parameters at the end is used to avoid the "parameter not used inside the function body" error, although you already use these parameters. This is required to compile the function successfully.
|
When calling nlf_FuncName to reuse built-in functions, the syntax is:
- nlf_FuncName( independent variable, parameter list ... )
where FuncName is the fitting function name. Besides, the old notation, nlfxFuncName also supported.
The Parameter List follows the parameter order in function definition file for the built-in function (the FDF file. You can open the FDF file in Notepad. The files are located in the \\Origin EXE Folder\FitFunc\). Note that, the function name we use is the DLL interface name. The actual name in the [General Information] section of the FDF file. Look at the Function Source item and the value is fgroup.FuncName, and use the FuncName. In most cases, this function name is consistent with the function name visible in the NLFit dialog. For a few few functions such as Voigt, these names are different.
For parameter initialization of this skewed gaussian function, we can simply copy the initialization code of the built-in gauss function, and make a few minor modifications:
xc = peak_pos(x_y_curve, &w1, &y0, &A1);
w2 = w1;
A2 = A1;
The final function body should be as below:
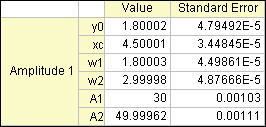
Once compiled successfully, save the function and fit the curve. The results should be as below:
|