4.2.2.24 Fitting Integral Function with a Sharp PeakFitting-Integral-SharpPeak
Summary
In this tutorial, we will show you how to define an integral fitting function with a sharp peak in the integral function, and perform a fit of the data using this fitting function.
Because the integral function contains a sharp peak, the integral should be performed in three segments so that the sharp peak can be integrated in a narrow interval.
Minimum Origin Version Required: Origin 9.0 SR0
What you will learn
This tutorial will show you how to:
- Define an integral fitting function.
- Integrate a function with a sharp peak.
- Divide the integral interval into several segments.
Example and Steps
Import Data
- Open a new workbook.
- Copy data in Sample Data to the workbook.
- Highlight column B, and select Plot: Symbol: Scatter from Origin menu. The graph should look like:
Define Fitting Function
The fitting integral function is described as follows:
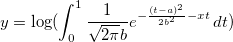
where a and b are parameters in the fitting function.
Initial parameters are: a=1e-4, b=1e-4. Note that the integral function contains a peak whose center is about a and width is 2b. And the peak's width (2e-4) is very narrow compared with the integral interval [0,1]. To make sure it is integrated correctly at the neighborhood of the peak center, the integral interval [0,1] is divided into three segments: [0,a-5*b], [a-5*b,a+5*b], [a+5*b,1]. It is integrated in each segment, and then the three integrals are summed up.
The fitting function can be defined using the Fitting Function Builder tool.
- Select Tools: Fitting Function Builder from Origin menu.
- In the Fitting Function Builder dialog's Goal page, click Next button.
- In the Name and Type page, select User Defined from Select or create a Category drop-down list, type fintpeak in the Function Name field, and select Expression in Function Type group, check Include Integration During Fitting check box. And click Next button.
- In the Integrand page, type myint in Integrand Name edit box, t in Integration Variable edit box and a, b, x in Arguments edit box. Type the following script in Integrand Function box.
return 1/(sqrt(2*pi)*b)*exp(-(t-a)^2/(2*b^2)-x*t);
And click Next button.
- In the Variables and Parameters page, type a, b in the Parameters field. Click Next button.
- In the Expression Function page, click Parameters tab, and set Initial Value for parameters a and b to 1e-4, click Integrand tab, and set Value for Lower Limit and Upper Limit to 0 and 1, Value for a, b, x to a, b, x respectively.
- In the Expression Function page, click Insert button. In the Quick Check group, type 0 in x= edit box, click Evaluate button, and it shows y=9.3e-21. This implies that the peak is not integrated correctly because y should approach 1 for x=0. Divide the integral into three segments, and type following script in Function Body box.
integral(myint, 0, a-5*b, a ,b ,x)+integral(myint, a-5*b, a+5*b, a ,b ,x)+
integral(myint, a+5*b, 1, a ,b ,x)
Click Evaluate button again, and it shows y=0.84, hence it is clear that the peak is integrated correctly this time.
- In the Expression Function page, update the script in Function Body box as follows.
log(integral(myint, 0, a-5*b, a ,b ,x)+integral(myint, a-5*b, a+5*b, a ,b ,x)
+integral(myint, a+5*b, 1, a ,b ,x))
Click Finish button.
Fit the Curve
- Select Analysis: Fitting: Nonlinear Curve Fit from Origin menu. In the NLFit dialog, select Settings: Function Selection, in the page select User Defined from the Category drop-down list and fintpeak function from the Function drop-down list. Note that initial parameters have been set during defining the fitting function.
- Click Fit button to fit the curve.
Fitting Results
The fitted curve should look like:

Fitted Parameters are shown as follows:
| Parameter
|
Value
|
Standard Error
|
| a
|
4.98302E-4
|
1.07593E-5
|
| b
|
1.94275E-4
|
8.21815E-6
|
The Adj. R-Square is 0.99799. Thus the fitting result is very good.
Sample Data
| x
|
y
|
| 0
|
-0.00267
|
| 60
|
-0.01561
|
| 240
|
-0.05268
|
| 500
|
-0.10462
|
| 1000
|
-0.22092
|
| 1500
|
-0.31004
|
| 2000
|
-0.40695
|
| 3000
|
-0.61328
|
| 4000
|
-0.75884
|
| 5000
|
-0.9127
|
| 6000
|
-0.98605
|
| 7000
|
-1.18957
|
| 9000
|
-1.43831
|
| 10000
|
-1.41393
|
| 12000
|
-1.61458
|
| 15000
|
-1.88098
|
| 20000
|
-2.07792
|
|