フィットしながら総和を求める
サマリー
NAGライブラリを使って、積分込みのフィットを実行する方法を学習しましたが、今回はNAG関数を使わずに行う方法を学習します。このチュートリアルでは、作成するフィット関数に総和を求める手順を含め、台形法則に基づいて積分を行う方法を学習します。
必要なOriginのバージョン:8.0 SR6
学習する項目
サンプルとステップ
NAGライブラリを使った積分フィットと同じモデルを使ってフィットします。
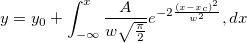
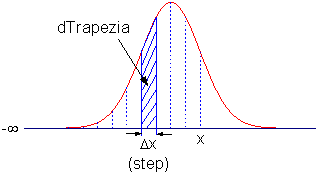
違いは、フィット関数の中で積分を実行することです。台形法則を使うため、最初に曲線を小さい区間に分け、複数の台形から積分を近似します。結果の精度は使用する台形の数に依存します。これは片側無限の積分なので、増分(ステップ)をセットし、上側積分限界をx、下側積分限界を負の無限大にして台形を作成し、これらの台形の面積の累計を計算します。面積の増分が十分に小さくなったら、総和の計算を中止します。総和を行う前に、関数が収束していることを保証するか、収束チェックをコードに含める必要があります。
関数を定義する
ツール:フィット関数オーガナイザと選択するかF9キーを押して フィット関数オーガナイザを開き、関数を次のように定義します。
-
| |
|
| 関数名: |
summation |
| 実現方式: |
UserDefined |
| 独立変数: |
x |
| 従属変数: |
y |
| パラメータの名前: |
y0, A, xc, w |
| 定義形式: |
Origin C |
| 関数: |
|
関数ボックスの横にあるボタン(アイコン)をクリックして、コードビルダを開きます。フィット関数の定義、コンパイル、保存を次のように行います。
#pragma warning(error :15618)
#include <origin.h>
// 被積分関数の為のサブルーチン
double f(double x, double A, double xc, double w)
{
return A * exp(-2*(x-xc)*(x-xc)/w/w) / w / sqrt(PI/2);
}
//----------------------------------------------------------
//
void _nlsfsummation(
// フィットパラメータ:
double y0, double A, double xc, double w,
// 独立変数:
double x,
// 従属変数:
double& y)
{
// 編集可能部分の開始
// 積分中止の許容値をセット
double dPrecision = 1e-12;
// 初期化
double dIntegral = 0.0;
double dTrapezia = 0.0;
// ステップまたは精度
double dStep = 0.01;
//台形法則による積分実行
// 関数が収束したことを保証
do
{
// 台形の面積
dTrapezia = 0.5 * ( f(x, A, xc, w) + f((x-dStep), A, xc, w) ) * dStep;
// 面積の累計
dIntegral += dTrapezia;
x -= dStep;
}while( (dTrapezia/dIntegral) > dPrecision );
// y値のセット
y = y0 + dIntegral;
// 編集部分の終了
}
曲線をフィットする
結果を比較するために同じデータを使うこともできます。
- Samples\Curve Fitting\Replicate Response Data.dat をインポートします。
- 最初の列を選択し、コンテキストメニューから列値の設定を選択します。
- 列値の設定ダイアログに
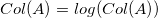 とセットします。これはシグモイド曲線を作成します。 とセットします。これはシグモイド曲線を作成します。
- 列AとBを選択し、散布図を作成します。
- そして、Ctrl + Yを押し、NLFitダイアログを開きます。先ほど定義したフィット関数を選択し、パラメータタブに移動して、すべてのパラメータを1で初期化し、フィットします。以下のような結果になります。
-
| |
値 |
標準誤差 |
| y0 |
-0.00806 |
0.18319 |
| A |
3.16479 |
0.39624 |
| xc |
-0.19393 |
0.10108 |
| w |
1.7725 |
0.33878 |
|