2種類の関数を使ってコンボリューションフィットを行うFitting-Convolution-2Funcs
概要
このチュートリアルでは、2つの関数を使用したコンボリューションフィットを行う方法と、等間隔ではないXデータをこの関数でフィットする方法を示します。
 | もし、使うデータがGaussと指数関数のコンボリューションの場合、組み込み関数であるPeak Functionsカテゴリ内にあるGaussModを使って直接データをフィットできます。
|
必要なOriginのバージョン:Origin 9.0 SR0以降
学習する項目
このチュートリアルでは、以下の項目について解説します。
- 関数を作成する
- 二つの関数のコンボリューションを計算する
- フィット関数の定数を定義する
- コンボリューション前に0でパッドする
- 不均等なX値に対してコンボリューション結果を補間する
- パラメータを使用して精度とスピードのバランスをとる
- Yエラーバーを重み付けとして利用する
サンプルとステップ
データのインポート
- 新しいワークブックを用意します。ヘルプ: フォルダを開く: サンプルフォルダを選択して、サンプルフォルダを開きます。このフォルダ内のCurve FittingサブフォルダにあるConvData.dat ファイルを探します。空のワークシートにファイルをドラッグアンドドロップしてインポートします。列Aは等間隔ではないことが分かります。LabTalkのdiff関数を使って真偽を確かめられます。
- 列Cで右クリックし、ショートカットメニューから列XY属性の設定:Yエラーバーを選択します。 列Bと列Cを選択し、メニューから作図: シンボル図:散布図:下・左軸と操作します。グラフは次のようになります。
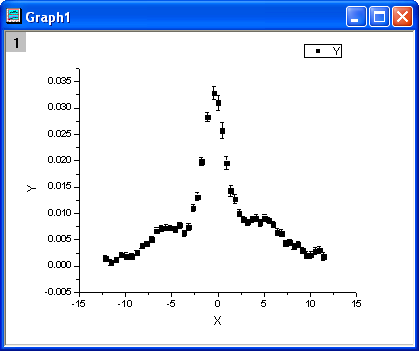
フィット関数を定義する
フィット関数は2関数のコンボリューション関数を使用します。以下のように表記することができます。
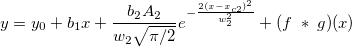
上記において、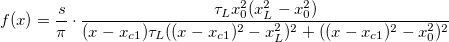 です。 です。
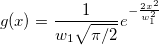 . .
そして 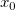 , , 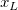 , , 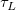 , s, , s, 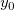 , , 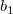 , , 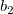 はフィットパラメータです。 はフィットパラメータです。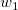 , , 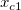 , , 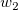 , , 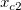 , , 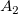 はフィット関数内の定数です。 はフィット関数内の定数です。
フィット関数は、フィット関数ビルダーを使用して定義できます。
- メニューから、ツール:フィット関数ビルダーを選択します。
- フィット関数ビルダーダイアログの処理のゴールページで進むのボタンをクリックします。
- 関数名と関数形式のページでは、関数カテゴリーの選択ドロップダウンリストでUser Definedを選択し、関数名をconvfuncとします。また、関数形式はOrigin Cにします。そして、進むボタンをクリックします。
- 変数とパラメータページでは、x0,xL,tL,s,y0,b1,b2 をパラメータエリアに入力し、 w1,xc1,w2,xc2,A2を定数エリアに入れます。進むをクリックします。
- OriginCフィット関数ページでは、次のように初期パラメータを設定します。
x0 = 3.1
xL = 6.3
tL = 0.4
s = 0.14
y0 = 1.95e-3
b1 = 2.28e-5
b2 = 0.2
定数タブをクリックし、定数を以下のように設定します。
w1 = 1.98005
xc1 = -0.30372
w2 = 5.76967
xc2 = 3.57111
A2 = 9.47765e-2
関数内容ボックスの右にあるボタン  をクリックし、コードビルダで次のようにフィット関数を定義します。 をクリックし、コードビルダで次のようにフィット関数を定義します。
ヘッダファイルを含みます。
#include <ONLSF.H>
#include <fft_utils.h>
関数本体を定義します。
NLFitContext *pCtxt = Project.GetNLFitContext();
if ( pCtxt )
{
// 各反復はVector型で返します。
static vector vX, vY;
static int nSize;
BOOL bIsNewParamValues = pCtxt->IsNewParamValues();
// パラメータが更新されると、コンボリューション結果を再計算します。
if ( bIsNewParamValues )
{
//サンプリング間隔
double dx = 0.05;
vX.Data(-16.0, 16.0, dx);
nSize = vX.GetSize();
vector vF, vG, vTerm1, vTerm2, vDenominator, vBase, vAddBase;
double Numerator = tL * x0^2 * (xL^2 - x0^2);
vTerm1 = ( (vX - xc1) * tL * ( (vX - xc1)^2 - xL^2 ) )^2;
vTerm2 = ( (vX - xc1)^2 - x0^2 )^2;
vDenominator = vTerm1 + vTerm2;
//関数 f(x)
vF = (s/pi) * Numerator / vDenominator;
//関数 g(x)
vG = 1/(w1*sqrt(pi/2))*exp(-2*vX^2/w1^2);
//コンボリューションを行う前に、 f と g にゼロをあてる
vector vA(2*nSize-1), vB(2*nSize-1);
vA.SetSubVector( vF );
vB.SetSubVector( vG );
//円形コンボリューションの実行
int iRet = fft_fft_convolution(2*nSize-1, vA, vB);
//最初と最後を切り取る
vY.SetSize(nSize);
vA.GetSubVector( vY, floor(nSize/2), nSize + floor(nSize/2)-1 );
//基線
vBase = (b1*vX + y0);
vAddBase = b2 * A2/(w2*sqrt(pi/2))*exp( -2*(vX-xc2)^2/w2^2 );
//フィットした Y
vY = dx*vY + vBase + vAddBase;
}
//コンボリューションの結果のフィットデータでxからyを補間する
ocmath_interpolate( &x, &y, 1, vX, vY, nSize );
}
コンパイルボタンをクリックして関数内容をコンパイルします。NLSFに戻るボタンをクリックします。
評価ボタンをクリックすると、x =1 でy=0.02165と表示されます。これは、定義した関数が正しい事を示しています。進むをクリックします。
- 進むをクリックします。境界条件と一般線形制約ページでは、境界条件を次のように設定します。
0 < x0 < 7
0 < xL < 10
0 < tL < 1
0 <= s <= 5
0 < b2 <= 3
完了ボタンをクリックします。
曲線をフィットする
- 解析: フィット:非線形曲線フィット をメニューから選択します。NLFitダイアログで、設定:関数選択を選び、カテゴリドロップダウンリストからUser Definedを選びます。そして関数ドロップダウンリストではconvfuncを選びます。 アクティブグラフ内でYエラーバーが表示されているので、列CがYの重み付けとして使われ、機械的ウェイト法がデフォルトで定義されています。
- フィットボタンをクリックし、フィットを行います。
フィット結果
フィット曲線のグラフは次のようになります。
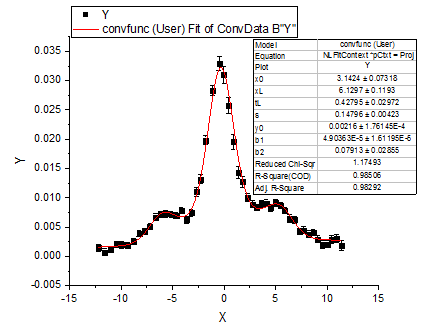
フィットパラメータは以下の通りです。
| パラメータ
|
値
|
標準誤差
|
| x0
|
3.1424
|
0.07318
|
| xL
|
6.1297
|
0.1193
|
| tL
|
0.42795
|
0.02972
|
| s
|
0.14796
|
0.00423
|
| y0
|
0.00216
|
1.76145E-4
|
| b1
|
4.90363E-5
|
1.61195E-5
|
| b2
|
0.07913
|
0.02855
|
フィット関数の本体ではdxに小さな値を入力でき結果はより正確になりますが、フィットが収束するまで時間がかかる事があります。
|