Mit der Faltung von zwei Funktionen anpassen
Fitting-Convolution-2Funcs
Zusammenfassung
In diesem Tutorial wird Ihnen gezeigt, wie Sie eine Faltung von zwei Funktionen definieren und eine Anpassung der Daten mit nicht äquidistant verteilten X-Werten mit Hilfe dieser Fitfunktion durchführen.
 |
Wenn Ihre Daten eine Faltung von Gauss- und Exponential-Funktionen darstellt, können Sie einfach die Standardanpassungsfunktion GaussMod in der Kategorie Peakfunktionen verwenden, um Ihre Daten direkt anzupassen.
|
Origin-Version mind. erforderlich: Origin 9.0 SR0
Was Sie lernen werden
Dieses Tutorial zeigt Ihnen, wie Sie:
- eine Funktion abtasten,
- eine Faltung von zwei Funktionen berechnen,
- Konstanten in der Anpassungsfunktion definieren,
- Nullen vor der Faltung auffüllen,
- das Faltungsergebnis für nicht äquidistant verteilte X-Werte interpolieren,
- einen Parameter verwenden, um die Geschwindigkeit und Genauigkeit im Gleichgewicht zu halten,
- den Y-Fehlerbalken als Gewichtung verwenden.
Beispiel und Schritte
Daten importieren
- Öffnen Sie eine leere Arbeitsmappe. Wählen Sie Hilfe: Ordner öffnen: Sample-Ordner ... im Menü, um den Ordner "Samples" zu öffnen. Öffnen Sie in diesem Ordner den Unterordner Curve Fitting und suchen Sie die Datei ConvData.dat. Ziehen Sie diese Datei per Drag&Drop in das leere Arbeitsblatt, um sie zu importieren. Beachten Sie, dass Spalte A nicht äquidistant verteilt ist. Wir können die LabTalk-Funktion diff verwenden, um dies zu verifizieren.
- Klicken Sie mit der rechten Maustaste auf Spalte C und wählen Sie Setzen als: Y-Fehlerbalken im Kontextmenü. Markieren Sie Spalte B und C und wählen Sie Zeichnen: Symbol: Punktdiagramm im Origin-Menü. Das Diagramm sollte folgendermaßen aussehen:
-
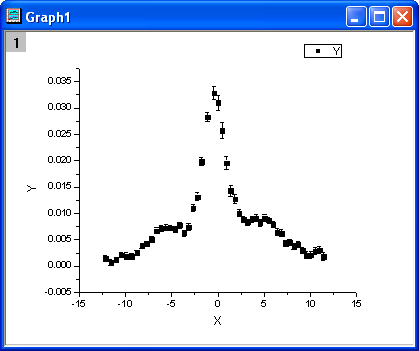
Anpassungsfunktion definieren
Die Anpassungsfunktion ist eine Faltung von zwei Funktionen. Sie kann wie folgt berechnet werden:
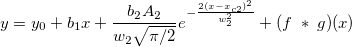
wobei 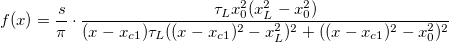 , ,
-
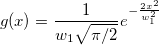 . .
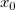 , , 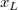 , ,  , s, , s, 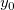 , , 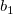 und und 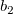 sind Anpassungsparameter. sind Anpassungsparameter. 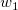 , , 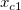 , , 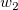 , , 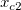 und und 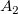 sind Konstanten in der Anpassungsfunktion. sind Konstanten in der Anpassungsfunktion.
Die Anpassungsfunktion kann mit Hilfe des Hilfsmittels Fitfunktionen erstellen definiert werden.
- Wählen Sie Hilfsmittel: Fitfunktionen erstellen im Origin-Menü.
- Klicken Sie im Dialog Fitfunktionen erstellen auf der Seite Ziel auf die Schaltfläche Weiter.
- Wählen Sie auf der Seite Name und Typ die Option User Defined in der Auswahlliste Eine Kategorie auswählen oder erstellen, geben Sie convfunc im Feld Funktionsname ein und wählen Sie Origin C in der Gruppe Funktionstyp. Klicken Sie auf die Schaltfläche Weiter.
- Geben Sie auf der Seite Variablen und Parameter die Parameter x0,xL,tL,s,y0,b1,b2 in das Feld Parameter ein und w1,xc1,w2,xc2,A2 in das Feld Konstanten. Klicken Sie auf Weiter.
- Legen Sie auf der Seite Origin C-Anpassungsfunktion die Initialisierungsparameter folgendermaßen fest:
x0 = 3,1 xL = 6,3 tL = 0,4 s = 0,14 y0 = 1,95e-3 b1 = 2,28e-5 b2 = 0,2
Klicken Sie auf die Registerkarte Konstanten und legen Sie die Konstanten, wie folgt, fest:
w1 = 1,98005 xc1 = -0,30372 w2 = 5,76967 xc2 = 3,57111 A2 = 9,47765e-2
Klicken Sie auf die Schaltfläche  rechts vom Bearbeitungsfeld des Funktionskörpers und definieren Sie die Anpassungsfunktion im Code Builder mit: rechts vom Bearbeitungsfeld des Funktionskörpers und definieren Sie die Anpassungsfunktion im Code Builder mit:
Headerdateien einschließen
#include <ONLSF.H> #include <fft_utils.h>
Funktionskörper definieren
NLFitContext *pCtxt = Project.GetNLFitContext(); if ( pCtxt ) { // Vector for the output in each iteration. static vector vX, vY; static int nSize; BOOL bIsNewParamValues = pCtxt->IsNewParamValues(); // If parameters were updated, we will recalculate the convolution result. if ( bIsNewParamValues ) { //Sampling Interval double dx = 0.05; vX.Data(-16.0, 16.0, dx); nSize = vX.GetSize(); vector vF, vG, vTerm1, vTerm2, vDenominator, vBase, vAddBase; double Numerator = tL * x0^2 * (xL^2 - x0^2); vTerm1 = ( (vX - xc1) * tL * ( (vX - xc1)^2 - xL^2 ) )^2; vTerm2 = ( (vX - xc1)^2 - x0^2 )^2; vDenominator = vTerm1 + vTerm2; //Function f(x) vF = (s/pi) * Numerator / vDenominator; //Function g(x) vG = 1/(w1*sqrt(pi/2))*exp(-2*vX^2/w1^2); //Pad zeroes at the end of f and g before convolution vector vA(2*nSize-1), vB(2*nSize-1); vA.SetSubVector( vF ); vB.SetSubVector( vG ); //Perform circular convolution int iRet = fft_fft_convolution(2*nSize-1, vA, vB); //Truncate the beginning and the end vY.SetSize(nSize); vA.GetSubVector( vY, floor(nSize/2), nSize + floor(nSize/2)-1 ); //Baseline vBase = (b1*vX + y0); vAddBase = b2 * A2/(w2*sqrt(pi/2))*exp( -2*(vX-xc2)^2/w2^2 ); //Fitted Y vY = dx*vY + vBase + vAddBase; } //Interpolate y from x for the fitting data on the convolution result. ocmath_interpolate( &x, &y, 1, vX, vY, nSize ); }
Klicken Sie auf die Schaltfläche Kompilieren, um den Funktionskörper zu kompilieren. Klicken Sie dann auf die Schaltfläche Zurück zum NSLF.
Klicken Sie auf die Schaltfläche Auswerten. Es wird y = 0,02165 bei x =1 angezeigt. Dies weist darauf hin, dass die definierte Fitfunktion korrekt ist. Klicken Sie auf Weiter.
- Klicken Sie auf Weiter. Setzen Sie auf der Seite Grenzen und allgemeine lineare Nebenbedingungen die folgenden Grenzen:
0 < x0 < 7 0 < xL < 10 0 < tL < 1 0 <= s <= 5 0 < b2 <= 3
Klicken Sie auf Fertigstellen.
| Hinweis: Um die angepassten Parameter zu überwachen, wurde die Klasse NLFitContext zum Definieren von Anpassungsfunktionen eingeführt, um einige Schlüsselinformationen innerhalb des Fitters zu erreichen. |
Kurve anpassen
- Wählen Sie Analyse: Anpassen: Nichtlinearer Fit im Origin-Menü. Wählen Sie im Dialog NLFit auf der Seite Einstellungen: Funktionsauswahl die Option User Defined in der Auswahlliste Kategorie und die Funktion convfun in der Liste Funktion. Beachten Sie, dass Y-Fehlerbalken im aktiven Diagramm gezeigt werden. Das heißt Spalte C wird als Y-Gewichtung verwendet, und Instrumental ist die standardmäßig ausgewählte Gewichtungsmethode.
- Klicken Sie auf die Schaltfläche Fit, um die Kurve anzupassen.
Anpassungsergebnisse
Die angepasste Kurve sollte folgendermaßen aussehen:
-
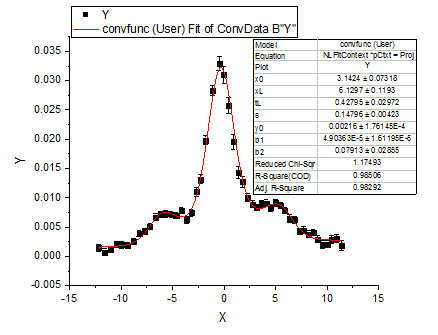
Die angepassten Parameter sind im Folgenden zu sehen:
| Parameter |
Wert |
Standardfehler |
| x0 |
3,1424 |
0,07318 |
| xL |
6,1297 |
0,1193 |
| tL |
0,42795 |
0,02972 |
| s |
0,14796 |
0,00423 |
| y0 |
0,00216 |
1,76145E-4 |
| b1 |
4,90363E-5 |
1,61195E-5 |
| b2 |
0,07913 |
0,02855 |
Beachten Sie, dass Sie einen kleineren Wert für dx im Fitfunktionskörper einsetzen können. Dadurch wird das Ergebnis vielleicht genauer, allerdings benötigt die Anpassung möglicherweise mehr Zeit.
|