Anpassen mit zwei Integralen mit Hilfe der LabTalk-FunktionFitting-2Integral-LabTalk
Zusammenfassung
Unter bestimmten Umständen möchten Sie vielleicht eine Fitfuntkion mit mehreren Integralen erstellen:
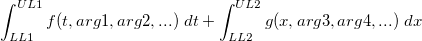
Bitte lesen Sie unter Anpassen mit Integral mit Hilfe der LabTalk-Funktion eine genauere Beschreibung der Parameter in dem Ausdruck nach. In Version Origin 8.6 unterstützt die Funktion Fitfunktionen erstellen jedoch nur ein Integral in der Fitfunktion. Durch Umgehen des komplexen Origin C-Codes können Sie die Funktion Fitfunktionen verwalten verwenden, um das Ziel zu erreichen. In diesem Tutorial sehen Sie, wie Sie mit der Funktion Fitfunktionen verwalten eine Fitfunktion erstellen, die aus zwei Integralen besteht. Natürlich ist es möglich, je nach Bedarf mehr Integrale einzubinden.
Origin-Version mind. erforderlich: Origin 8.6
 | Seit Origin 2018b können Sie eine implizite Funktion mit Hilfe von Integralen definieren. |
Was Sie lernen werden
Dieses Tutorial zeigt Ihnen, wie Sie:
- eine Anpassungsfunktion mit Hilfe des Dialogs Fitfunktionen verwalten erstellen.
- eine Fitfunktion mit zwei Integralen mit Hilfe einer LabTalk-Funktion erstellen.
Beispiel und Schritte
Das Anpassungsmodell
Das Anpassungsmodell wird wie folgt geschrieben
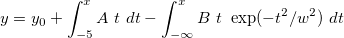
In der Anpassungsfunktion gibt es vier Parameter. Um eine Integration durchzuführen, müssen drei von ihnen an den Integrand weitergegeben und die unabhängige Variable als obere Grenze verwendet werden.
Die Funktion definieren
- Drücken Sie F9, um den Dialog Fitfunktionen verwalten zu öffnen. Fügen Sie eine neue Funktion hinzu, indem Sie auf Neue Funktion klicken, nachdem Sie eine Kategorie für Ihre neue Funktion ausgewählt haben. Es ist ebenfalls möglich, eine neue Kategorie hinzufügen, indem Sie auf die Schaltfläche Neue Kategorie klicken.
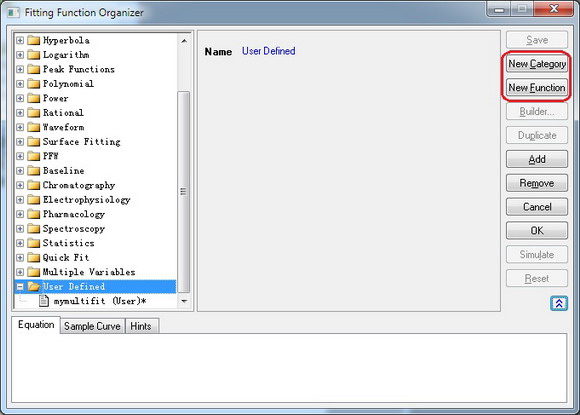
- Legen Sie den Funktionsnamen im Bearbeitungsfeld Funktionsname fest. Definieren Sie Unabhängige Variablen, Abhängige Variablen und Parameternamen in den entsprechenden Bearbeitungsfeldern.
- Wählen Sie die Funktionsform in dem Auswahlfeld aus. Erklärungen finden Sie auf der Registerkarte Hinweise unten im Dialog aufgeführt.
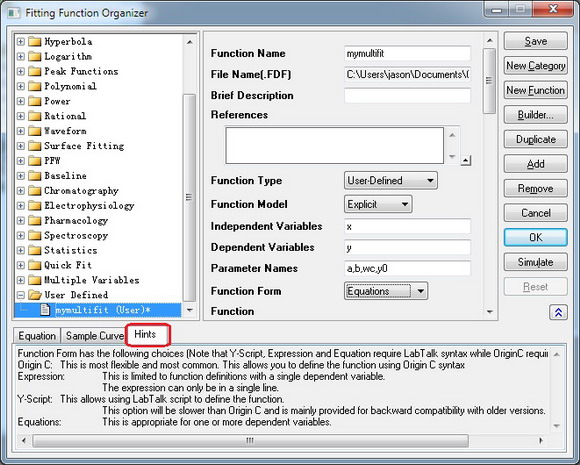
- Definieren Sie im Bearbeitungsfeld Funktion Ihre Fitfunktion. Die Integrale werden in Form der LabTalk-Integralfunktion geschrieben.
y=integral(polyint, -5, x, a)-integral(gaussint, -inf, x, b, wc)+y0
Wie unter Anpassen mit Integral mit Hilfe der LabTalk-Funktion beschrieben, sind x, a, b und wc Parameter, die an die Integrandfunktionen weitergegeben werden.
- Klicken Sie auf die Schaltfläche rechts oben im Feld Parametereinstellungen, um den Dialog Parametereinstellungen zu aktivieren. Legen Sie die Initialisierungswerte sowie weitere Nebenbedingungen wie die unteren Grenzen und oberen Grenzen für jeden Parameter fest.
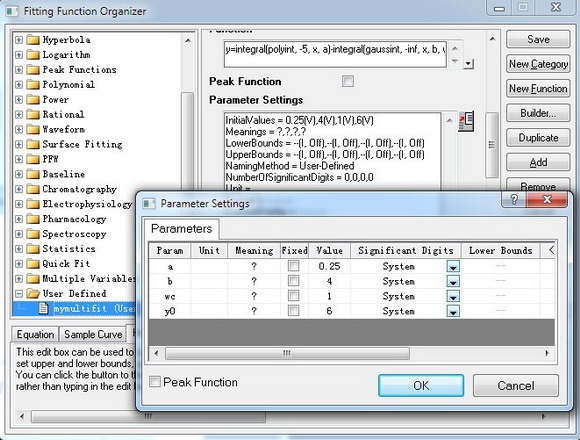
- Definieren Sie die zwei Integrale in dem Feld LabTalk-Funktionsdefinitionen und -Initialisierungen. In diesem Fall sollten die Funktionen folgendermaßen aussehen:
function double polyint(double t, double ia) { return ia*t; } function double gaussint(t, ib, iwc) { return ib *t* exp(-(t)^2/iwc^2); }
- Sie haben erfolgreich die Fitfunktion mit den zwei Integralen erstellt. Weitere Informationen können in dem entsprechenden Feld vermerkt werden. Vergessen Sie nicht, Ihre Fitfunktion zu speichern, nachdem Sie fertig sind.
Kurve anpassen
Kopieren Sie die folgenden Daten und fügen Sie sie in ein Origin-Arbeitsblatt ein:
| X |
Y |
| -3 |
2.47613 |
| -2.6 |
2.24016 |
| -2.2 |
2.01543 |
| -1.8 |
1.83094 |
| -1.5 |
1.85038 |
| -1.1 |
2.17725 |
| -0.9 |
2.44967 |
| -0.7 |
2.61423 |
| -0.5 |
3.02305 |
| -0.3 |
3.23057 |
| -0.1 |
3.37822 |
| 0. 1 |
3.2827 |
| 0.3 |
3.18775 |
| 0.5 |
2.86194 |
| 0.7 |
2.69104 |
| 0.9 |
2.39315 |
| 1.4 |
2.04046 |
| 1.8 |
1.85287 |
| 2.2 |
1.85325 |
| 2.6 |
2.20569 |
Markieren Sie Y-Spalte und drücken Sie Strg + Y, um den Dialog NLFit aufzurufen. Wählen Sie die Funktion, die Sie gerade definiert haben, und klicken Sie auf die Schaltfläche Fit  , um die Anpassung durchzuführen. , um die Anpassung durchzuführen.
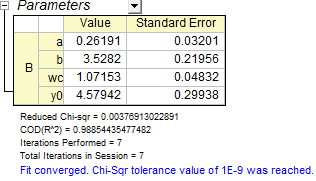
|