有理関数のパラメータ初期化
RationalFunc-InitialParameter
サマリー
このチュートリアルでは、複数線形回帰法を使って有理フィット関数の初期パラメータを計算する方法を示します。また、計算された初期パラメータを使用してフィットを実行します。
必要なOriginのバージョン: Origin 9.0 SR0以降
学習する項目
このチュートリアルでは、以下の項目について解説します。
- 有理フィット関数用の初期パラメータを計算する
- OriginCのコードを使って複数の線形回帰を行う
サンプルとステップ
アルゴリズム
このチュートリアルでは、次の有理関数を例として使用します。
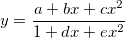
xは独立変数、yは従属変数、a, b, c, d, eは全てフィットパラメータです。
両辺を右辺の分母で掛けると、次のようになります。
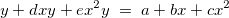
この数式は次のように表現できます。
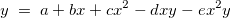
フィットデータ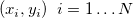 を数式に代入すると、次のようになります。 を数式に代入すると、次のようになります。
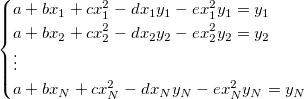
よって、有理多項フィット関数の初期パラメータを推定するのは、線形係数としてa, b, c, d, eを持つ、複数の線形回帰の問題に変形します。つまり、次のような式になります。
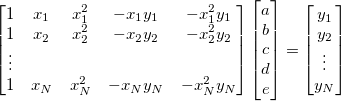
Originは複数線形回帰のための関数ocmath_複数線形回帰をOriginCから提供しており、初期化コードで呼び出すことができます。
データのインポート
- 新規ワークブックを作成します。
- サンプルデータ の内容をワークブックにコピーします。
- 列Bを選択し、メニューから作図: シンボル図:散布図 と操作します。グラフは次のようになります。
-
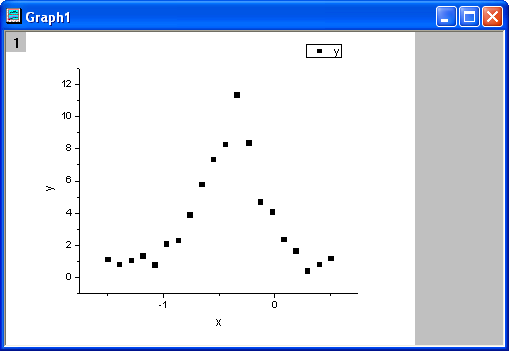
フィット関数の定義と初期化パラメータ
フィット関数は、フィット関数ビルダーツールを使用して定義できます。
- メニューから、ツール:フィット関数ビルダーを選択します。
- フィット関数ビルダーダイアログの処理のゴールページで進むのボタンをクリックします。
- 関数名と関数形式のページでは関数カテゴリーの選択/新規名称のドロップダウンリストからUser Definedを選択します。次に関数名のエリアに rationalfuncと入力し、関数形式で算術式を選びます。進むボタンをクリックします。
- 変数とパラメータのページでは、パラメータエリアにa, b, c, d, eを入力します。進むボタンをクリックします。
- 式形式の関数ページで、以下のスクリプトを関数内容編集ボックスに入力します。
(a+b*x+c*x^2)/(1+d*x+e*x^2)
評価ボタンをクリックすると、x=1の時にy=1であると示しているので、数式は正しいことを示しています。進むボタンをクリックします。
- パラメータ初期化ルーチンページでは、初期化コードボックスの右側にある、コードビルダを開くボタン
 をクリックします。フィットパラメータをalgorithmの記述に沿って初期化します。 をクリックします。フィットパラメータをalgorithmの記述に沿って初期化します。
UINT nOSizeN = x_data.GetSize(); //ポイントの数
UINT nVSizeM = 5; //パラメータの数
matrix mX(nOSizeN, 5);
//独立変数のデータポイントのための行列を作成する
vector vCa(nOSizeN), vCb, vCc, vCd, vCe;
vCa = 1;
mX.SetColumn( vCa, 0 );
vCb = x_data;
mX.SetColumn( vCb, 1 );
vCc = x_data^2;
mX.SetColumn( vCc, 2 );
vCd = -x_data*y_data;
mX.SetColumn( vCd, 3 );
vCe = -x_data^2*y_data;
mX.SetColumn( vCe, 4 );
//複数の線形回帰オプション
LROptions stLROptions;
stLROptions.UseReducedChiSq = 1;
stLROptions.FixIntercept = 1; //交点を0に固定FitParameter stFitParameters[ 6 ]; // nVSizeM+1 となるはずです
UINT nFitSize = nVSizeM + 1;
int nRet = ocmath_multiple_linear_regression(mX, nOSizeN, nVSizeM, y_data,
NULL, 0, &stLROptions, stFitParameters, nFitSize );
if( nRet == STATS_NO_ERROR )
{
a = stFitParameters[1].Value;
b = stFitParameters[2].Value;
c = stFitParameters[3].Value;
d = stFitParameters[4].Value;
e = stFitParameters[5].Value;
}
コンパイルボタンをクリックしてファイルをコンパイルします。NLSFに戻るボタンをクリックします。完了をクリックして、フィット関数ビルダーダイアログを閉じます。
曲線をフィットする
- 解析:フィット:非線形曲線フィットをメニューから選択します。NLFitダイアログで、設定:関数選択を選び、カテゴリドロップダウンリストからUser Definedを選びます。そして関数ドロップダウンリストではrationalfuncを選びます。
- パラメータタブをクリックします。パラメータタブを開くと、初期化コードから初期化パラメータが計算されてダイアログにあらかじめ入力されます。そして、初期パラメータ用のフィット関数は次のようになります。初期化コードから算出された初期パラメータはとても良いようです。
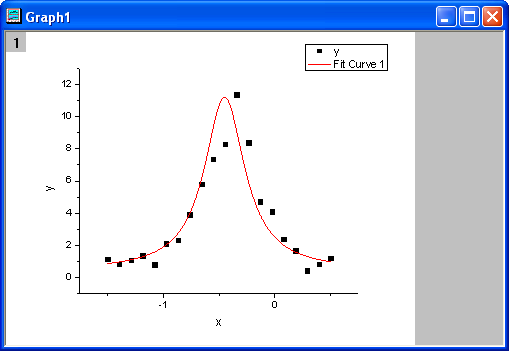
- フィットボタンをクリックし、フィットを行います。
フィット結果
フィット曲線は次のようになります。
-
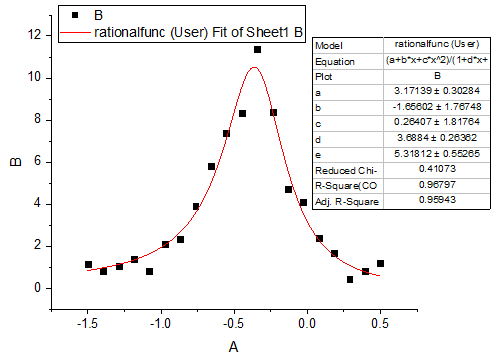
フィットパラメータは以下の通りです。
| パラメータ |
値 |
標準誤差 |
| a |
3.17139 |
0.30284 |
| b |
-1.65602 |
1.76748 |
| c |
0.26407 |
1.81764 |
| d |
3.6884 |
0.26362 |
| e |
5.31812 |
0.55265 |
サンプルデータ
| x |
y |
| -1.5 |
1.13173 |
| -1.39474 |
0.8262 |
| -1.28947 |
1.06999 |
| -1.18421 |
1.37155 |
| -1.07895 |
0.79569 |
| -0.97368 |
2.11346 |
| -0.86842 |
2.32006 |
| -0.76316 |
3.9205 |
| -0.65789 |
5.81904 |
| -0.55263 |
7.38037 |
| -0.44737 |
8.31272 |
| -0.34211 |
11.39718 |
| -0.23684 |
8.39808 |
| -0.13158 |
4.7305 |
| -0.02632 |
4.11105 |
| 0.07895 |
2.39105 |
| 0.18421 |
1.65394 |
| 0.28947 |
0.42953 |
| 0.39474 |
0.83337 |
| 0.5 |
1.18758 |
| Noteこの方法を使って、他の有理多項フィット関数のパラメータも初期化できます。 |
|