NAGライブラリを使ってパラメータ制限がある積分関数をフィットする
サマリー
このチュートリアルを始める前に、NAGライブラリを使った積分フィットを読むことをお薦めします。そして、プログラミングに関する部分については、2つのチュートリアルは基本的に同じで、異なる点は、ここでは積分制限を持つフィットパラメータでのOrigin Cのフィット関数を定義することを学びますが、前のチュートリアルでは、積分制限での独立変数を定義します。また、ここでは別のNAG積分関数が使われています。
必要なOriginのバージョン:8.0 SR6
学習する項目
このチュートリアルでは、以下の項目について説明します。
- NAGの積分ルーチンを使って、定積分でのフィット関数を作成します。
- パラメータの積分制限を持つフィット関数を作成します。
- log関数を使って、フィット関数から大きな戻り値のスケールに合わせます。
サンプルとステップ
例えば、次のモデルを使って、このページの一番下にあるサンプルデータ をフィットしましょう。
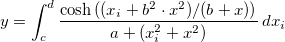
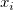 を使って積分の独立変数を示していますが、  はフィッティングの独立変数を示していることに注意して下さい。モデルのパラメータ ,  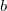,  ,  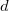は、サンプルデータから取得したいフィットパラメータです。データを準備するには、サンプルデータをOriginのワークシートにコピーする必要があります。フィットの手順は、前のチュートリアルと同じように行います。
フィット関数オーガナイザでフィット関数を定義する
F9 を押して、フィット関数オーガナイザを開き、最初のチュートリアルと同様に、ユーザ定義の積分フィット関数 nag_integration_fitting_cosh をカテゴリーFittingWithIntegral に追加します。
-
| |
|
| 関数名： |
nag_integration_fitting_cosh |
| 実現方式： |
ユーザ定義 |
| 独立変数： |
x |
| 従属変数： |
y |
| パラメータの名前： |
a, b, c, d |
| 定義形式： |
Origin C |
| 関数： |
|
「関数」ボックスの近くにあるボタン(アイコン)をクリックしてコードビルダを開き、次のようにフィット関数を定義して、コンパイルします。（Note:コンパイル後に関数を保存して関数オーガナイザダイアログに戻る事を忘れないでください。）
#include <origin.h>
// ここにincludeファイルを追加します。
// 例えば、NAGライブラリからの関数でフィットする場合、
// ここにNAG関数のヘッダファイルを追加します。
#include <oc_nag8.h>
// このファイルに定義したい他のOrigin C関数に対するコードをここに追加し、
// フィット関数でアクセスできるようにします。
struct user
{
double a, b, fitX; // fitX はフィット関数の独立変数です。
};
static double NAG_CALL f_callback(double x, Nag_User *comm) // x は被積分関数の独立変数です。
{
struct user *sp = (struct user *)(comm->p);
double aa, bb, fitX; // 一時変数としてNag_User 通信構造体のパラメータとして受け入れます
aa = sp->a;
bb = sp->b;
fitX = sp->fitX;
return cosh((x*x+bb*bb*fitX*fitX)/(bb+fitX))/(aa+(x*x+fitX*fitX));
}
// 他のファイルがワークスペースにロードされ、コンパイルされていれば、
// そのファイルで定義されているC関数にアクセスでき、関数は上記でインクルードした
//ヘッダファイルにプロトタイプがあります。
// 関数コード内でNLSFオブジェクトのプロパティとメソッドにアクセスできます。
// 関数の定義には、C言語のシンタックスを使います。
// 例えば、パラメータ名がP1の場合、関数定義に p1 と使うことはできません。
// 分数を使用する場合には、1/2のような整数の除算は0になり、0.5ではありません。
// 正しい値にするには、0.5または1/2.0を使います。
// より詳細な情報およびサンプルは、Originヘルプファイルの「ユーザ定義フィット関数」
// を参照してください。
//----------------------------------------------------------
//
void _nlsfnag_integration_fitting(
// フィットパラメータ:
double a, double b, double c, double d,
// 独立変数:
double x,
// 従属変数:
double& y)
{
// 編集可能部分の開始
double epsabs = 0.00001, epsrel = 0.0000001, result, abserr;
Integer max_num_subint = 500;
// epsabsとepsrel、およびこの値を使って必要な精度に向上できるので、
// 必要な積分の精度を制御できます。
Nag_QuadProgress qp;
static NagError fail;
// integrand のパラメータを初期化するのにcall_back 関数を利用でき、
// 上記を行うには Nag_User 通信構造体を通して行います。
Nag_User comm;
struct user s;
s.a = a;
s.b = b;
s.fitX = x;
comm.p = (Pointer)&s;
d01sjc(f_callback, c, d, epsabs, epsrel, max_num_subint, &result, &abserr, &qp, &comm, &fail);
// エラーメッセージを出力することで、エラーを調査するには、以下の行のコメントを解除します。
// if (fail.code != NE_NOERROR)
// printf("%s\n", fail.message);
// 次の3つのエラー以外は、入力パラメータが不正であるか
//アロケーションエラーに当たります： NE_INT_ARG_LT NE_BAD_PARAM NE_ALLOC_FAIL
// メモリーリークを避けるため、積分ルーチンを呼ぶ前にメモリのアロケーションを
// 解放する必要があります。
if (fail.code != NE_INT_ARG_LT && fail.code != NE_BAD_PARAM && fail.code != NE_ALLOC_FAIL)
{
NAG_FREE(qp.sub_int_beg_pts);
NAG_FREE(qp.sub_int_end_pts);
NAG_FREE(qp.sub_int_result);
NAG_FREE(qp.sub_int_error);
}
y = log(result);
// 積分の対数結果を返すのは容量が大きくなることもあるので、
// 必ずしも行う必要はありません
// 編集可能部分の終了
}
上記のコードでは、フィット関数 _nlsfnag_integration_fitting_coshの本体の外側で被積分関数をコールバック関数 f_callback として定義しています。被積分関数を変数 a, b , fitX でパラメータ化し、それらを Nag_User 構造体を使ってコールバック関数に渡します。その後、NAG積分ルーチン d01sjcを使って、積分を実行します。上記以外にも求積ルーチン を希望に合わせて利用する事ができます。現在のサンプルでは、フィット関数に対数スケールを使います。(サンプルデータは、既に対数関数でスケーリングされています。)
コードをコンパイルし、ダイアログに戻り、フィット関数オーガナイザでフィット関数を保存し、「解析：フィット」メニューから「非線形曲線フィット」ダイアログを開きます。そして、「設定」タブの「関数選択」ページで、このユーザ定義のフィット関数を選択することができます。
パラメータの初期値をセットする
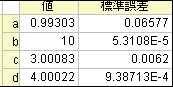
ユーザ定義のフィット関数なので、パラメータの初期値を指定する必要があります。非線形曲線フィットダイアログの「パラメータ」タブで手動でセットすることもできます。今回の例では、パラメータの初期値を  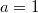,  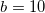,  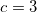,  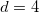のようにセットします。パラメータが初期化されると、以下に示すようにフィットを実行して、フィット結果を取得することができます。
サンプルデータ
-
| サンプルデータ |
結果 |
| X |
Y |
 |
| -5 |
498.19046 |
| -4.33333 |
329.43196 |
| -3.66667 |
210.28005 |
| -3 |
126.55799 |
| -2.33333 |
69.01544 |
| -1.66667 |
31.3555 |
| -1 |
9.1393 |
| -0.33333 |
-0.84496 |
| 0.33333 |
-0.99914 |
| 1 |
6.86736 |
|