LabTalk関数を使った積分フィット
Fitting-Integral-LabTalk
サマリー
バージョンOrigin 8.6からOriginは一元積分を行える新しいLabTalkの関数、integral()を取り入れました。この関数は次のような積分の値を算出します。
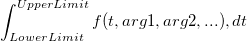
integral()関数のインターフェイスは次のように定義されています。
-
integral(integrandName, LowerLimit, UpperLimit [, arg1, arg2, ...])
ここではintegrandNameはこの被積分関数の関数名になります。
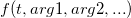
言い方を変えると、integral()関数は以下について行います。
- 他の関数を(第一アーギュメントとして)被積分関数に受け入れます。
- 定義された下限および上限に積分を行い、正数値を算出します。
- 必要に応じ、積分関数に後続の引数(Arg1, Arg2, ...)を追加することができます。
この機能を利用すると、integral()関数を使ってフィット関数を定義でき、正しいフィットパラメータを被積分関数に受け渡して積分曲線のフィットにあたります。
このチュートリアルでは以下のチュートリアル、NAG関数を呼び出しフィット中に積分を行うをLabTalk用に変更し、いかにシンプルに積分関数を使用してフィットできるかをお見せします。
必要なOriginのバージョン: Origin 8.6 以降
 |
Origin 2018bから、積分を使って陰函数を定義することができます
|
学習する項目
このチュートリアルでは、以下の項目について解説します
- フィット関数ビルダーでフィット関数を作成する
- Labtalk関数を使って積分定義を組み込んだフィット関数を定義する
- フィット関数の初期化コードをセットアップする
サンプルとステップ
フィッティングモデル
フィッティングモデルは次の式で表されます。
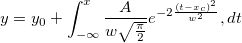
フィット関数には4つのパラメータがあり、そのうち3つを被積分関数に受け渡し、独立変数を上限として積分を行います。よって、まず被積分関数を定義しし、それをもとにintegral() 関数を使用してフィット関数内で積分をします。
関数を定義する
- F8を押してフィット関数ビルダダイアログを開きます。新しい関数の作成が選ばれていることを確認してから進むボタンを押して次のページに進みます。
- 関数名と関数形式ページで関数名をMyIntegGaussと設定します。関数タイプはデフォルトの算術式のままで、フィット中に積分を実行にチェックをします。進むをクリックして、次のページに行きます。
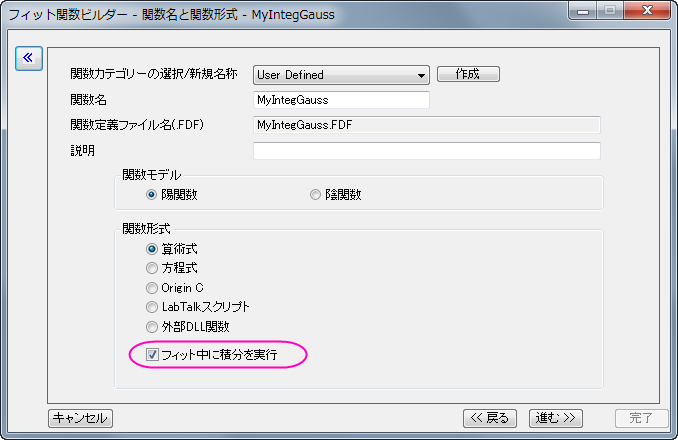
- 被積分関数ページでは、被積分関数の表現を定義できます。現在、Originは一元積分のみをサポートしているので、積分変数は1つのみです。この例では被積分関数の式は以下のようになります。
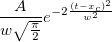
他の変数、xc、w、Aは被積分関数のパラメータになります。Tパラメータと区別するためにここでは引数として名前を付けます。よって、これらの引数はixc、iw、iAとなります。後程、フィットパラメータをこれらの引数に受け渡します。そのため、被積分関数は次のようになります。
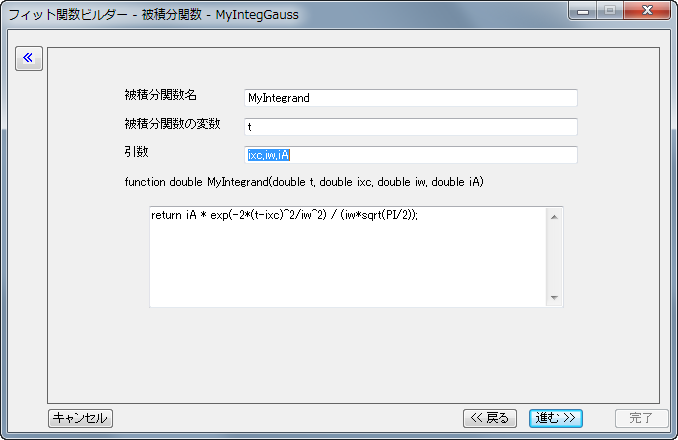
これはLabTalkの関数であることに注意してください。積分値を入手するには関数内の定義にリターン(RETURN)記述が必要です。この例の中の被積分関数表現は次のようになります。
return iA * exp(-2*(t-ixc)^2/iw^2) / (iw*sqrt(PI/2));
- 設定ができたら進むをクリックして変数とパラメータページへ進みます。そこで、下図のようにフィット関数の変数とパラメータを定義します。
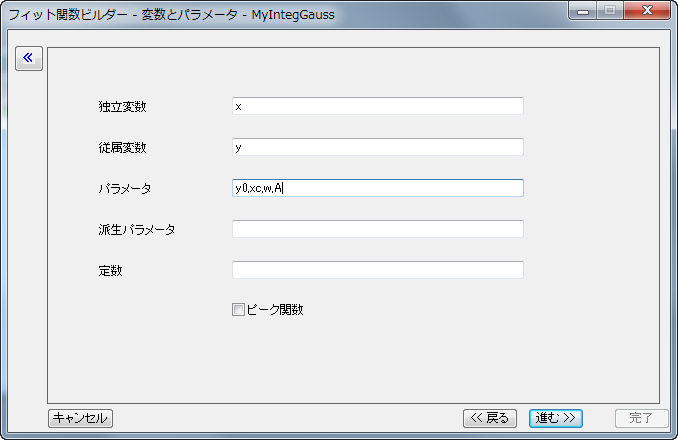
- 次の関数ページがフィット関数式の内容を定義するページです。フィット関数に積分を組み込むものをフィット関数ビルダ―ウィザードで設定すると、追加タブである被積分関数がこのページに表示されます。このタブでは、下限、上限、および積分の引数を含む、被積分変数とパラメータを被積分関数の要素で指定できます。この例では次のように変数の対応付けをします。
| 被積分関数の要素 |
被積分関数に受け渡す値 |
| 下限 |
-inf |
| 上側限界 |
x |
| ixc |
xc |
| iw |
w |
| iA |
A |
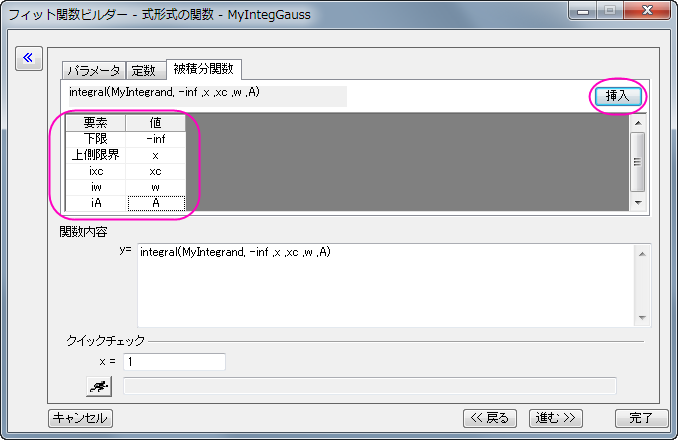
上記表のように対応ができたら挿入 ボタンを押します。すると、準備したintegral() 関数が関数式ボックス内に以下のように挿入されます。
integral(MyIntegrand, -inf ,x ,xc ,w ,A)
この数式は「MyIntegrandという関数にマイナス無限数からxまでを積分し、xc、w、Aという3つのパラメータを被積分関数に送る」という意味です。
ここで定数パラメータy0を数式に入れると、全体のフィット関数内容は次のようになります。
y0 + integral(MyIntegrand, -inf, x, xc ,w ,A);
そしてページは次のようになります。
- パラメータタブをアクティブにし、適切な初期値を次のように設定します。
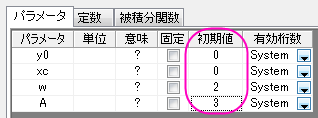
完了ボタンを押してこのフィット関数を保存します。
曲線をフィットする
次のデータ をOriginの新しいワークシートにコピー&ペーストします。
-
| X |
Y |
| -1.69897 |
0.13136 |
| -1.22185 |
0.34384 |
| -0.92082 |
0.6554 |
| -0.82391 |
0.73699 |
| -0.69897 |
1.00157 |
| 0 |
1.70785 |
| 0.30103 |
2.31437 |
| 0.69897 |
2.77326 |
| 1 |
2.79321 |
Y列を選択し、Ctrl + YキーでNLFitダイアログを開きます。先程定義した関数を選び、フィット ボタンをクリックしてフィットを行います。このフィットの結果はNAG関数を直接利用したものと同じになります。
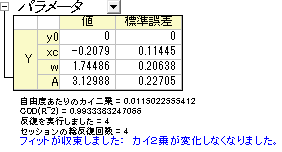
|