Anpassung mit stückweisen Funktionen

Zusammenfassung

Wir zeigen Ihnen in diesem Tutorial, wie Sie stückweise Anpassungsfunktionen definieren.

Origin-Version mind. erforderlich: 8.0 SR6

Was Sie lernen werden

Dieses Tutorial zeigt Ihnen, wie Sie:

• Stückweise (bedingte) Anpassungsfunktionen definieren.

Beispiel und Schritte

Starten Sie dieses Tutorial, indem Sie die Datei \Samples\Curve Fitting\Exponential Decay.dat importieren. Markieren Sie die Spalte D und zeichnen Sie ein Punktdiagramm. Diese Kurve kann mit vielen Standardfunktionen der Kategorie Growth/Sigmoidal angepasst werden. In diesem Tutorial teilen wir die Kurve jedoch in zwei Teile mit einer stückweisen Funktion.

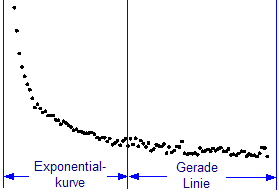
Die Gleichung ist daher:

Definieren der Funktion

Drücken Sie F9, um den Fit-Funktions-Manager zu öffnen und eine Funktion zu definieren:

Funktionsname:	piecewise
Funktionstyp:	Benutzerdefiniert
Unabhängige Variable:	x
Abhängige Variable:	y
Parameternamen:	xc, a, b, t1
Funktionsform:	Origin C
Funktion:

Klicken Sie auf die Schaltfläche rechts vom Bearbeitungsfeld der Funktion und definieren Sie die Anpassungsfunktion im Code Builder mit:

void _nlsfpiecewise(
// Fit Parameter(s):
double xc, double a, double b, double t1,
// Independent Variable(s):
double x,
// Dependent Variable(s):
double& y)
{
        // Beginning of editable part
        // Divide the curve by if condition.
        if(x<xc) {
                y = a+b*x+exp(-(x-xc)/t1);
        } else {
                y = a+b*x;
        }
        // End of editable part
}

Anpassen der Kurve

Drücken Sie Strg + Y, um das Dialogfeld NLFit bei aktiver Grafikseite aufzurufen. Wählen Sie die Funktion piecewise, die wir definiert haben, und initialisieren Sie die Parameterwerte mit:

xc:	1
a:	1
b:	-1
t1:	0,1

Klicken Sie auf die Schaltfläche Fit, um die Ergebnisse zu erzeugen.

xc:	0,24
a:	36,76585
b:	-24,62876
t1:	0,04961

Beachten Sie, dass diese Funktion auf xc und t1 reagiert, d.h., unterschiedliche Initialisierungswerte können unterschiedliche Ergebnisse erzeugen.