Mit Integral anpassen unter Verwendung der NAG-Bibliothek
Fitting-Integral-NAG
Zusammenfassung
Mit Origin können Anwender eine Origin C-Anpassungsfunktion definieren,
die ein Integral beinhaltet. Sie können NAG-Funktionen aufrufen, um die
Integration durchzuführen, während die Anpassungsfunktion definiert wird.
Es gibt standardmäßige Funktionen in Origin C, die Integration durchführen.
Für das aktuelle Beispiel wird die NAG-Lösung empfohlen. Sie verfügt über
eine bessere Durchführung im Vergleich zum standardmäßigen Integrationsalgorithmus.
Beachten Sie, das hier ein unendlicher NAG-Integrator verwendet
wird.
Origin-Version mind. erforderlich: Origin 8.0 SR6
Was Sie lernen
werden
Dieses Tutorial zeigt Ihnen, wie Sie:
- eine Anpassungsfunktion mit Hilfe des Dialogs Fitfunktionen verwalten
erstellen.
- eine Anpassungsfunktion mit endlichem Integral mit Hilfe der NAG-Integrationsroutine
erstellen.
- den Initialisierungscode für die Anpassungsfunktion einrichten.
Beispiel und
Schritte
Wir passen das folgende Modell an:
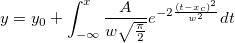
Hier sind 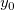 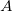 , , 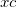 und und 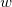 die Modellparameter, die wir aus der Datenanpassung
erhalten möchten. Der Anpassungsprozess kann in den folgenden Schritten
zusammengefasst werden: die Modellparameter, die wir aus der Datenanpassung
erhalten möchten. Der Anpassungsprozess kann in den folgenden Schritten
zusammengefasst werden:
Funktion definieren
Drücken Sie F9, um den Dialog Fitfunktionen verwalten
zu öffnen und eine neue Kategorie mit dem Namen FittingWithIntegral
zu erstellen. Definieren Sie folgendermaßen eine neue Anpassungsfunktion
nag_integration_fitting in der neuen Kategorie:
| Funktionsname: |
nag_integration_fitting |
| Funktionstyp: |
Benutzerdefiniert |
| Unabhängige Variable: |
x |
| Abhängige Variable: |
y |
| Parameternamen: |
y0, A, xc, w |
| Funktionsform: |
Origin C |
| Funktion: |
|
Klicken Sie auf die Schaltfläche  neben dem Feld Funktion, um den
Code Builder zu öffnen. Folgen Sie dann den Schritten unten: neben dem Feld Funktion, um den
Code Builder zu öffnen. Folgen Sie dann den Schritten unten:
-
Scrollen Sie nach oben bis zu der Zeile
//add the header file for the NAG functions here.
und fügen Sie den folgenden Code unter dieser Zeile ein.
#include <oc_nag8.h>
-
Gehen Sie zur Zeile
// and access in your fitting function.
und fügen Sie den folgenden Code darunter ein.
struct user // parameters in the integrand
{
double amp, center, width;
};
// Function supplied by user, return the value of the integrand at a given x.
static double NAG_CALL f_callback(double x, Nag_User *comm)
{
struct user *sp = (struct user *)(comm->p);
double amp, center, width; // temp variable to accept the parameters in the Nag_User communication struct
amp = sp->amp;
center = sp->center;
width = sp->width;
return amp * exp( -2*(x - center)*(x - center)/width/width ) / (width*sqrt(PI/2));
}
-
Gehen Sie zur Zeile
// Beginning of editable part.
und fügen Sie den folgenden Code darunter ein.
// Through the absolute accuracy epsabs, relative accuracy epsrel and max_num_subint you can
// control the precision of the integration you need
// if epsrel is set negative, the absolute accuracy will be used.
// Similarly, you can control only relative accuracy by set the epsabs negative
double epsabs = 0.0, epsrel = 0.0001;
// The max number of sub-intervals needed to evaluate the function in the integral
// The more difficult the integrand the larger max_num_subint should be
// For most problems 200 to 500 is adequate and recommended
Integer max_num_subint = 200;
// Result keeps the approximate integral value returned by the algorithm
// abserr is an estimate of the error which should be an upper bound for the |I - result|
// where I is the integral value
double result, abserr;
// The structure of type Nag_QuadProgress,
// it contains pointers allocated memory internally with max_num_subint elements
Nag_QuadProgress qp;
// The NAG error parameter (structure)
static NagError fail;
// Parameters passed to integrand by Nag_User communication struct
Nag_User comm;
struct user s;
s.amp = A;
s.center = xc;
s.width = w;
comm.p = (Pointer)&s;
// Perform integration
// There are 3 kinds of infinite boundary types you can use in Nag infinite integrator
// Nag_LowerSemiInfinite, Nag_UpperSemiInfinite, Nag_Infinite
d01smc(f_callback, Nag_LowerSemiInfinite, x, epsabs, epsrel, max_num_subint, &result, &abserr, &qp, &comm, &fail);
// you may want to exam the error by printing out error message, just uncomment the following lines
// if (fail.code != NE_NOERROR)
// printf("%s\n", fail.message);
// For the error other than the following three errors which are due to bad input parameters
// or allocation failure NE_INT_ARG_LT NE_BAD_PARAM NE_ALLOC_FAIL
// You will need to free the memory allocation before calling the integration routine again to avoid memory leakage
if (fail.code != NE_INT_ARG_LT && fail.code != NE_BAD_PARAM && fail.code != NE_ALLOC_FAIL)
{
NAG_FREE(qp.sub_int_beg_pts);
NAG_FREE(qp.sub_int_end_pts);
NAG_FREE(qp.sub_int_result);
NAG_FREE(qp.sub_int_error);
}
// Calculate the fitted value
y = y0 + result;
- Klicken Sie auf Kompilieren, um die Datei zu kompilieren.
In dem obenstehenden Code definieren Sie zuerst den Integrand als eine
Rückfragefunktion f_callback außerhalb des Anpassungsfunktionskörpers
_nlsfnag_integration_fitting. Beachten Sie, dass wir die
Integrandfunktion mit den Variablen amp, center
und width parametrisieren und sie in die Rückfragefunktion
durch Nag_User weitergeben. Innerhalb der Anpassungsfunktion führen
wir die Integration mit Hilfe des NAG-Integrators d01smc
durch.
Das Aufrufen von NAG-Funktionen sollte effizienter sein als das Schreiben
Ihrer eigenen Routinen. Mit Hilfe einer analogen Methode können Sie endliche,
unendliche, eindimensionale und mehrdimensionale Qadraturen in Ihrer Anpassungsfunktion
durchführen. Lesen Sie bitte die Seite NAG
Quadrature und wählen Sie eine geeignete Routine aus.
Initialisierungswerte für die Parameter festlegen oder
Initialisierungscode einrichten
Da es sich um eine benutzerdefinierte Anpassungsfunktion handelt, müssen
Sie die Initialisierungsschätzwerte für die Parameter zur Verfügung stellen.
Sie können dies später tun, indem Sie sie manuell auf der Registerkarte
Parameter im Dialog NLFit festlegen.
Simulieren
der Funktion
Nach Eingabe der Funktionskörpercodes können Sie auf die Schaltfläche
Kompilieren im Code Builder klicken, um Syntaxfehler zu
prüfen. Klicken Sie dann auf die Schaltfläche Zum Dialog zurückkehren,
um zum Dialog Fitfunktionen verwalten zurückzukehren.
Klicken Sie jetzt auf die Schaltfläche Speichern, um die .FDF-Datei
(Funktionsdefinitionsdatei) zu erzeugen.
Sobald Sie eine .FDF-Datei haben, können Sie auf die Schaltfläche Simulieren
klicken, um eine Kurve zu simulieren. Dies ist bei der Bewertung der Initialisierungswerte
sehr hilfreich. Geben Sie im Dialog simcurve einige entsprechende
Parameterwerte und den X-Bereich ein und sehen Sie im Vorschaufeld,
wie die Kurve aussehen wird.
Kurve anpassen
Bevor Sie mit der Anpassung der Kurve starten, ist es sehr hilfreich,
die Funktion zuerst zu simulieren. Die Durchführung der Integration kann
einige Zeit dauern, aber falls ein Fehler auftritt, können Sie sehen,
wie Origin "einfriert", nachdem Sie auf die Schaltfläche Fit
klicken. Wählen Sie in dem Dialog Fitfunktionen verwalten
die Funktion, die Sie definiert haben, und klicken Sie auf die Schaltfläche
Simulieren. Dies öffnet die X-Funktion simcurve. Geben Sie
einige "Schätz"werte ein und klicken Sie auf die Schaltfläche
Anwenden. Wenn die simulierte Kurve aussieht wie Ihre Quelldaten,
können Sie mit der Anpassung fortfahren.
Um die Anpassungsfunktion festzulegen:
- Importieren Sie \Samples\Curve Fitting\Replicate Response Data.dat
in Origin.
- Als Nächstes verwenden Sie die Log-Skalierung der Daten in Spalte
Col(A). Dazu geben Sie in der Beschriftungszeile F(x) = von Spalte
A die Formel Col(A) = log(Col(A)) ein und drücken Sie Enter
einmal, um die Daten zu ändern.
- Markieren Sie Spalte A und B und erstellen Sie ein Punktdiagramm.
Die Form entspricht einer eine sigmoidalen Kurve.
- Rufen Sie den Dialog NLFit im Menü Analyse:
Anpassen: Nichtlinearer Fit auf.
- Wählen Sie die Anpassungsfunktion aus, die Sie gerade definiert
haben, und gehen Sie zur Registerkarte Parameter. Initialisieren
Sie alle Parameter mit 1 und führen Sie die Anpassung durch (klicken Sie
auf die Schaltfläche Fit).
- Sie sollten diese Ergebnisse sehen:
|
|
Wert |
Standardfehler |
|---|
| y0 |
-0,00806 |
0,18319 |
|---|
| A |
3,16479 |
0,39624 |
|---|
| xc |
-0,19393 |
0,10108 |
|---|
| w |
1,77252 |
0,33878 |
|---|
|