FAQ-782 Warum bleibt der Standardfehler des Parameters unverändert, wenn der Fehlerbalken sich stark verändert?
Chi-Se-Remain
Letztes Update: 08.08.2018
Um den Standardfehler (SE) des angepassten Parameters und die verwandten Ergebnisse, die mit anderer Software kompatibel sind, beizubehalten, ist das Kontrollkästchen Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) standardmäßig aktiviert. Bei aktiviertem Kontrollkästchen bleibt der Standardfehler SE des Parameters der gleiche, auch wenn die Fehlerbalken sich stark verändern. Wir empfehlen, diese Option zu deaktivieren, wenn Daten mit instrumenteller Gewichtung, beliebigem Datensatz oder direkter Gewichtung angepasst werden, so dass der Standardfehler des Parameters den Betrag der Gewichtung wiedergeben kann.
Das Kontrollkästchen Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) ist auch hier zu finden:
-
|
Hinweis:
Dieses Kontrollkästchen beeinflusst NUR den Standardfehler der angepassten Parameter. Es beeinflusst NICHT den Anpassungsprozess oder die Parameterwerte in irgendeiner Weise.
|
Einfache Erklärung der Theorie
Wir erläutern unten, wie der SE des j-ten angepassten Parameters 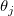 sich mit oder ohne Aktivierung von Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) ändert. Der Einfachheit halber nehmen wir an, dass der Fehlerbalken sich mit oder ohne Aktivierung von Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) ändert. Der Einfachheit halber nehmen wir an, dass der Fehlerbalken 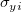 , multipliziert mit einer Konstanten k skaliert ist. Einzelheiten zu Algorithmus bzw. Erklärung finden Sie unter die Theorie der nichtlinearen Kurvenanpassung. , multipliziert mit einer Konstanten k skaliert ist. Einzelheiten zu Algorithmus bzw. Erklärung finden Sie unter die Theorie der nichtlinearen Kurvenanpassung.
Wenn das Kontrollkästchen Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) aktiviert ist, hängt die Varianz-Kovarianz-Matrix 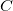 für Parameter für Parameter 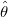 per Standard sowohl von per Standard sowohl von 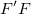 als auch von als auch von 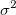 ab. ab.
Wobei 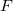 die partielle Ableitungsmatrix ist, deren Element in der i-ten Zeile und der j-ten Spalte folgendermaßen lautet: die partielle Ableitungsmatrix ist, deren Element in der i-ten Zeile und der j-ten Spalte folgendermaßen lautet:
und 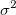 ist die mittlere Residuenvarianz, die vom reduzierten Chi-Quadrat geschätzt wird: ist die mittlere Residuenvarianz, die vom reduzierten Chi-Quadrat geschätzt wird:
SE von 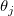 ist dann die Quadratwurzel des Werts einer Hauptdiagonalen der Matrix ist dann die Quadratwurzel des Werts einer Hauptdiagonalen der Matrix 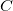
Wenn die Fehlerbalken 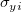 mit einem Faktor k geändert werden, werden sowohl mit einem Faktor k geändert werden, werden sowohl 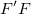 als auch als auch 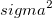 mit einem Faktor mit einem Faktor 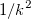 geändert. k wird sie dann jeweils in der Berechnung des Standardfehlers aufheben. Daher bleibt der Standardfehler unverändert, wenn der Fehlerbalken skaliert wird. geändert. k wird sie dann jeweils in der Berechnung des Standardfehlers aufheben. Daher bleibt der Standardfehler unverändert, wenn der Fehlerbalken skaliert wird.
Wenn Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) deaktiviert ist, wird 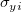 beim Berechnen der Varianz-Kovarianz-Matrix ausgeschlossen und die Matrix beim Berechnen der Varianz-Kovarianz-Matrix ausgeschlossen und die Matrix 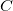 hängt nur von hängt nur von 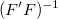 ab. ab.
SE wird jetzt
Wenn die Fehlerbalken mit k multipliziert werden, wird der SE auch mal k sein.
Nach Anpassen der Modelle verwenden wir das reduzierte Chi-Quadrat, um zu prüfen, ob die Gewichtungen den realen Y-Fehler darstellen können oder nicht. Zusammengefasst: Wenn Sie herausfinden, dass der Standardfehler des Parameters sich sehr unterscheidet bei Aktivierung bzw. Deaktivierung des Kontrollkästchens Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.), bedeutet dies, dass die Gewichtungen möglicherweise nicht die realen Y-Fehler darstellen. Weitere Informationen finden Sie auf dieser Seite.
Schnelles Beispiel
Unten befindet sich ein kurzes Beispiel, das belegt, dass Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) nur den Standardfehler der angepassten Parameter beeinflusst.
- Kopieren Sie diese Daten und fügen Sie in ein Arbeitsblatt ein.
- Klicken Sie mit der rechten Maustaste auf die Spalte col(C) und wählen Sie Setzen als: Als Y-Fehler setzen.
- Markieren Sie alle Spalten und wählen Sie Analyse: Anpassen: Nichtlinearer Fit, um den Dialog NLFit zu öffnen.
- Wählen Sie Gauss in der Auswahlliste Funktion. Gehen Sie zur Registerkarte Erweitert und erweitern Sie den Zweig Fit-Steuerung. Stellen Sie sicher, dass das Kontrollkästchen Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) aktiviert ist.
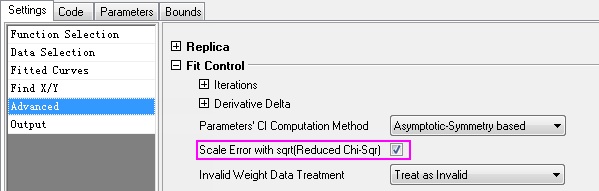
Wenn Sie auf Fit klicken, wird ein Anpassungsbericht erzeugt, der Parameterwerte und Standardfehler enthält.
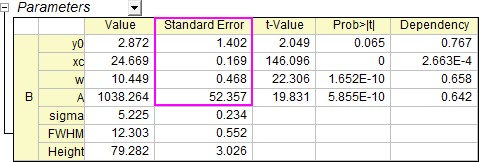
- Klicken Sie auf das grüne Schloss und wählen Sie Parameter ändern. Deaktivieren Sie im Dialog NLFit das Kontrollkästchen Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.).
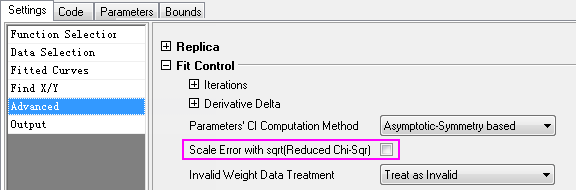
Klicken Sie auf Fit. Standardfehler der Parameter ändern sich, aber die angepassten Werte nicht.
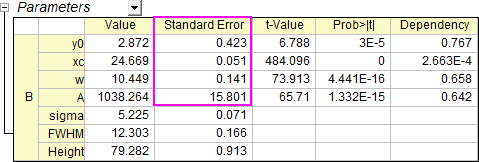
- Jetzt wird der Fehler skaliert und festgestellt, wie unterschiedlich der Einfluss auf den Standardfehler ist je nachdem, ob Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) aktiviert ist oder nicht. Öffnen Sie den Dialog NLFit über Parameter ändern. Aktivieren Sie Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) und ändern Sie die Einstellung für Neu berechnen in Auto.
- Multiplizieren Sie die Fehlerspalte C mit 10. Das Berichtsblatt wird automatisch aktualisiert. Sie sehen, dass der Standardfehler (SE) der Parameter der gleiche bleibt (vergleichen Sie das zweite Bild in Schritt 4).
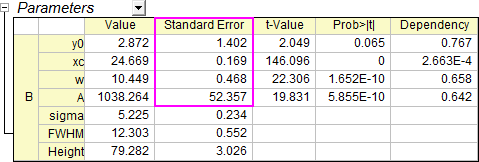
- Öffnen Sie den Dialog NLFit erneut über Parameter ändern. Deaktivieren Sie Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) Klicken Sie auf Fit. Sie sehen, dass der Standardfehler dieses Mal mit 10 multipliziert ist.
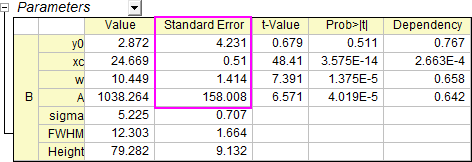
Beispieldaten
| X |
Y |
Y-Fehler |
| 11 |
5 |
0.4472 |
| 13 |
10 |
0.6324 |
| 15 |
19 |
0.8718 |
| 17 |
27 |
1.0392 |
| 19 |
49 |
1.4 |
| 21 |
65 |
1.6124 |
| 23 |
77 |
1.755 |
| 25 |
80 |
1.7888 |
| 27 |
77 |
1.755 |
| 29 |
59 |
1.5362 |
| 31 |
44 |
1.3266 |
| 33 |
24 |
0.9798 |
| 35 |
11 |
0.6634 |
| 37 |
14 |
0.7484 |
| 39 |
4 |
0.4 |
Schlüsselwörter:Anpassen, Standardfehler, reduziertes Chi-Quadrat, Fehlervarianz
|