3.127 FAQ-750 How can I calculate propagation delay time between two signals?Calculate-Propagation
Last Update: 10/13/2016
Assume we have two time-varying signal: Signal and Delay Signal, saved in worksheet column(B), column(D), respectively;
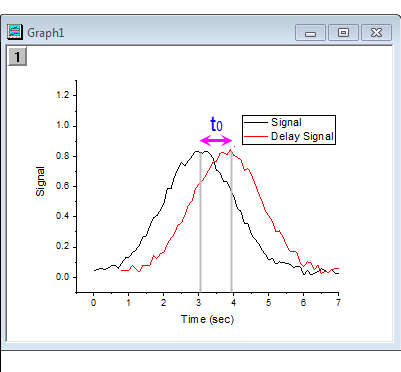
Assume we want to calculate the propagation delay between two signals, A model could be set up as below, f(t) is original signal while g(t) is delay signal.
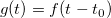
for all 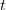 , and , and 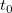 is a constant. is a constant.
Next, we will use the Nonlinear Curve Fit to calculate the 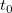 , a user defined fitting function can be constructed in this way: , a user defined fitting function can be constructed in this way:
The graph shown that the 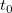 is approximate to 0.8, so the initial value for fitting can be set to 0.8. is approximate to 0.8, so the initial value for fitting can be set to 0.8.
| Function Name:
|
fitdelay
|
| Function Type:
|
User-Defined
|
| Independent Variables:
|
x
|
| Dependent Variables:
|
y
|
| Parameter Names:
|
t0
|
| Function Form:
|
Origin C
|
| Function:
|
#include <origin.h>
//
#include <ONLSF.H>
//
void _nlsffitdelay1(
// Fit Parameter(s):
double t0,
// Independent Variable(s):
double x,
// Dependent Variable(s):
double& y)
{
// Beginning of editable part
NLFitContext *pCtxt = Project.GetNLFitContext();
Worksheet wks;
DataRange dr;
int c1,c2;
dr = pCtxt->GetSourceDataRange(); //Get the source data range
dr.GetRange(wks, c1, c2); //Get the source data worksheet
if ( pCtxt )
{
static vector vX, vY;
static double nSize;
BOOL bIsNewParamValues = pCtxt->IsNewParamValues();
if ( bIsNewParamValues )
{
Dataset dsx(wks, 0);
Dataset dsy(wks, 1);
vX = dsx;
vY = dsy;
nSize = vY.GetSize();
}
double x1;
x1 = x-t0;
ocmath_interpolate( &x1, &y, 1, vX, vY, nSize );
}
// End of editable part
}
|
Please refer to this page for detailed steps about constructing user defined fitting function.
Fit the Curve
In the fitting function body, we read the response data directly from the active worksheet. So, you should perform the fit from the worksheet. Start with a new workbook and import the file \Samples\Curve Fitting\DelaySignal.dat
- Highlight column C and press Ctrl + Y to bring up the Nonlinear Fitting dialog.
- Go to the Function Selection page to select the fitdelay function you just defined.
- Click the Fit button to generate the results.
- The fitting results will be similar to this:
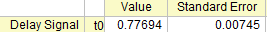
Keywords:Nonlinear Curve Fit, Signal Process
|