2.5.2.2 Algorithm: Nonparametric Distribution Analysis (Arbitrary Censoring)SA-Nonparametric-Dist-Algorithm
The Uncensor/Arbitrary Censor data are represented as time intervals  : :
-
 : lower bound (time of last inspection or last known survival) : lower bound (time of last inspection or last known survival)
-
 : upper bound (time when failure was first detected) : upper bound (time when failure was first detected)
- If
 , it represents right-censoring. , it represents right-censoring.
- If
 , it represents exact failure (uncensored). , it represents exact failure (uncensored).
Turnbull estimation method
Time intervals and the probabilities of each interval are calculated by the Turbull estimation[1]. Turnbull developed an iterative algorithm to obtain the nonparametric maximum likelihood estimate (NPMLE) of the cumulative distribution function for censored data. This approach is applicable to more general cases, including situations where the observation intervals overlap.
The covariance of the constrained MLE is computed via the Observed Fisher information matrix in the reduced parameter space[2] with the constraint  . .
Actuarial estimation method
First, a clinical life table is constructed, with each interval  representing the range into which survival times and times to loss or withdrawal are distributed. Each interval spans from representing the range into which survival times and times to loss or withdrawal are distributed. Each interval spans from  up to, but not including up to, but not including  for for  . The final interval extends to infinity. These intervals are considered fixed.
Using the input censoring information, we can tabulate the basic data required for the calculation. . The final interval extends to infinity. These intervals are considered fixed.
Using the input censoring information, we can tabulate the basic data required for the calculation.
-
 The midpoint of the The midpoint of the  th interval. th interval.
-
 The width of the The width of the  th interval. th interval.
-
 Number lost or withdrawn alive in the Number lost or withdrawn alive in the  th interval. th interval.
-
 Number die in the Number die in the  th interval. th interval.
-
 Number entering the ith interval Number entering the ith interval
-
 Number exposed to risk in the Number exposed to risk in the  th interval. th interval.
Actuarial Table
Conditional Probability of Failure
-

Varaince of Conditional Probability of Failure
-
![Var[\hat{q}_{i}]=\frac{\hat{q}_{i}(1-\hat{q}_{i})}{n_i} Var[\hat{q}_{i}]=\frac{\hat{q}_{i}(1-\hat{q}_{i})}{n_i}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/SA_Nonparametric_Dist_Algorithm/math-c829e89da580329b943d81ce9242197b.png?v=0)
Survival Probabilities
Cumulative Survival Probabilities
-
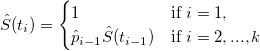
Variance of Cumulative Survival Probabilities
-
![Var[\hat{S}(t_i)] = [\hat{S}(t_i)]^2\sum_{j=1}^{i-1}\frac{\hat{q}_j}{n_j\hat{p}_j} Var[\hat{S}(t_i)] = [\hat{S}(t_i)]^2\sum_{j=1}^{i-1}\frac{\hat{q}_j}{n_j\hat{p}_j}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/SA_Nonparametric_Dist_Algorithm/math-2f967fd68cc2ee95b4febdf5574ad9b2.png?v=0)
Hazards and Densities
Hazard Estimates
-
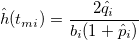
Variance of Hazards
-
![Var[\hat{h}(t_{mi})] = \frac{(\hat{h}(t_{mi}))^2}{n_i\hat{q}_i}(1-(\frac{1}{2}\hat{h}(t_{mi})b_i)^2) Var[\hat{h}(t_{mi})] = \frac{(\hat{h}(t_{mi}))^2}{n_i\hat{q}_i}(1-(\frac{1}{2}\hat{h}(t_{mi})b_i)^2)](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/SA_Nonparametric_Dist_Algorithm/math-ef2fbe1889f433cb1bc2f60be63f7550.png?v=0)
Probability Density Estimates
-

Variance of Probability Densities
-
![Var[\hat{f}(t_{mi})] = \frac{(\hat{S}(t_i)\hat{q}_i)^2}{b_i}\sum_{j=1}^{i-1}(\frac{\hat{q}_j}{n_j\hat{p}_j} + \frac{\hat{p}_j}{n_j\hat{q}_j}) Var[\hat{f}(t_{mi})] = \frac{(\hat{S}(t_i)\hat{q}_i)^2}{b_i}\sum_{j=1}^{i-1}(\frac{\hat{q}_j}{n_j\hat{p}_j} + \frac{\hat{p}_j}{n_j\hat{q}_j})](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/SA_Nonparametric_Dist_Algorithm/math-3316826d5e335ec292def4f9b228d6c5.png?v=0)
Characteristics of Variable
Median
-
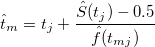
Variance of Median
-
![Var[\hat{t}_{m}] = \frac{\hat{S}(t_0)^2}{4n_0\hat{f}(t_{mj})} Var[\hat{t}_{m}] = \frac{\hat{S}(t_0)^2}{4n_0\hat{f}(t_{mj})}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/SA_Nonparametric_Dist_Algorithm/math-c3756195c735a00a966e9c645acc76e9.png?v=0)
Additional Time from Time T until Half of Units Fail
First find time interval  so that so that  and and  . Then . Then
-
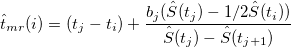
Variance of 
-
![Var[\hat{t}_{mr}(i)] = \frac{(\hat{S}(t_i))^2}{4n_i(\hat{f}(t_{mj}))^2} Var[\hat{t}_{mr}(i)] = \frac{(\hat{S}(t_i))^2}{4n_i(\hat{f}(t_{mj}))^2}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/SA_Nonparametric_Dist_Algorithm/math-d4e73a38c969afc4f1a7372f5985b9f2.png?v=0)
Confidence Interval
The confidence intervals are calculated using a normal approximation:
- Two-sided
 confidence interval confidence interval
-
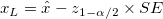
-
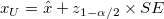
- One-sided
 lower confidence bound lower confidence bound
-
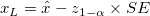
- One-sided
 upper confidence bound upper confidence bound
-
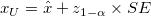
Reference
- B.W. Turnbull (1976). "The Empirical Distribution Function with Arbitrarily Grouped, Censored and Truncated Data". Journal of the Royal Statistical Society, 38: pp. 290-295.
- A. P. Dawid (1979). "Conditional independence in statistical theory." Journal of the Royal Statistical Society, Series B 41(1):1–31.
|