2.17 Probability Distribution Calculator (Pro)Probability-Distribution-Calculator
Summary
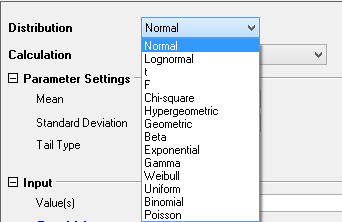
The tool Critical Value of Distributions is used to calculate critical values of common distributions, such as Normal, LogNormal, t, F, Chi-squared, Hypergeometric, Geometric, Beta, Exponential, Gamma, Weibull, Uniform, Binomial and Poisson. The critical values can be (1) probability density, (2) cumulative probability, and (3) values of inverse cumulative probabliity.
Examples
We want to calculate cumulative probability of Normal distribution at 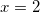 with parameters mean = 4 and standard deviation = 1. with parameters mean = 4 and standard deviation = 1.
- Install the tool if you haven't, then run script:
prob_dist_cal -d; or click the app icon Constrained Multiple Regression in App Gallery to open the app dialog
- Choose Normal for the Distribution;
- Choose Cumulative Probability for the Calculation;
- In the part of Parameter Settings: let Mean = 4 and Standard Deviation=1, and then choose Lower Tail for the Tail Type;
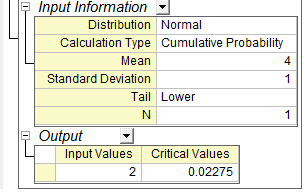
- In the part of Input: type 2. And we get the result is 0.0227501 below.
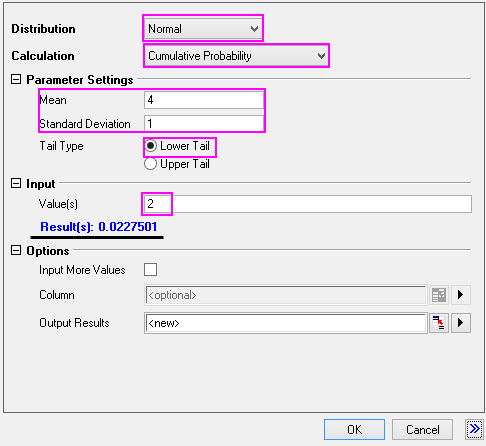
- Click OK to get the report table.
Dialog Settings
Distribution
Specify which distribution to concern. Normal, LogNormal, t, F, Chi-squared, Hypergeometric, Geometric, Beta, Exponential, Gamma, Weibull, Uniform, Binomial and Poisson distributions are available now.
Calculation
Specify which type of critical values to calculate.
- For continuous probability distributions such as Normal, LogNormal, t, F, Chi-squared, Beta, Exponential, Gamma, Weibull and Uniform, the values of probability density, cumulative probability, and inverse cumulative probability can be calculated.
- For discrete probability distributions such as Hypergeometric, Geometric, Binomial and Poisson, the values of probability density and cumulative probability can be calculated.

Parameter Settings
Set the values of parameters for the specific distribution chosen already.
For Cumulative Probability and Inverse Cumulative Probability settings, Tail Type option is available to specify which tail type to calculate. The meaning of Lower Tail and Upper Tail is obvious by seeing the figure in the Preview window right to the setting dialog.
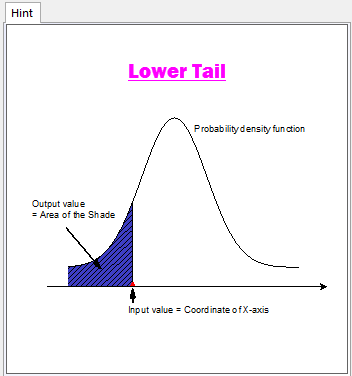 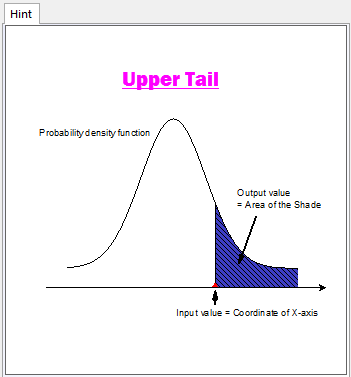
Input
Specify values at which the critical values of distribution are calculated. Several values can be input at the same time, separating by a space.

Options
Input more values from Worksheet and output the results.

Formulas
Normal distribution
The Normal distribution is also called Gaussian distribution. The probability density function is
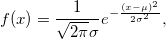
where 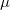 is the mean parameter; is the mean parameter; 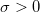 is standard deviation parameter; and is standard deviation parameter; and 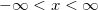 . .
Lognormal distribution
The probability density function is
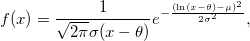
where 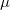 is the scale parameter; is the scale parameter; 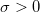 is location parameter; is location parameter; 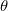 is threshold parameter; and is threshold parameter; and  . .
t distribution
The probability density function is
![f(x)=\frac{\Gamma[(v+1)/2]}{\Gamma(v/2)\sqrt{\pi v}}\left(1+\frac{x^2}{v}\right)^{-(v+1)/2}, f(x)=\frac{\Gamma[(v+1)/2]}{\Gamma(v/2)\sqrt{\pi v}}\left(1+\frac{x^2}{v}\right)^{-(v+1)/2},](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Probability_Distribution_Calculator/math-d70211ac7cc02d705e5201785e9d5afd.png?v=0)
where  is degree of freedom; and is degree of freedom; and 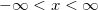 . . 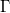 is the Gamma function. is the Gamma function.
F distribution
The probability density function is
![f(x)=\frac{\Gamma[(v+u)/2]}{\Gamma(v/2)\Gamma(u/2)} \left(\frac{u}{v}\right)^{u/2} x^{\frac{u}{2}-1} \left(1+\frac{u}{v}x\right)^{-(v+u)/2}, f(x)=\frac{\Gamma[(v+u)/2]}{\Gamma(v/2)\Gamma(u/2)} \left(\frac{u}{v}\right)^{u/2} x^{\frac{u}{2}-1} \left(1+\frac{u}{v}x\right)^{-(v+u)/2},](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Probability_Distribution_Calculator/math-d8a78d34fca977798fac234e57b244da.png?v=0)
where 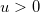 is numerator degree of freedom; is numerator degree of freedom;  is denominator degree of freedom; and is denominator degree of freedom; and 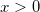 . .
Chi-squared distribution
The probability density function is
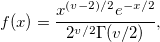
where  is degree of freedom; and is degree of freedom; and 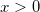 . .
Hypergeometric distribution
The probability density function is
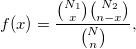
where 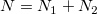 is population size; is population size; 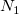 is number of events in the population; is number of events in the population; 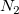 is number of nonevents in the population; is number of nonevents in the population;  is sample size; and is sample size; and  is number of events in the sample, s.t. is number of events in the sample, s.t.  . .
Geometric distribution
If the domain is 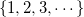 , then the probability density function is , then the probability density function is
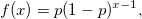
where 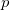 is event probability; and is event probability; and 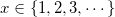 is the total number of trials. is the total number of trials.
If the domain is 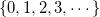 , then the probability density function is , then the probability density function is
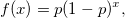
where 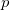 is event probability; and is event probability; and 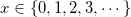 is the total number of nonevents occured before the first event is observed. is the total number of nonevents occured before the first event is observed.
Beta distribution
The probability density function is
![f(x)=\frac{\Gamma[\alpha+\beta]}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}, f(x)=\frac{\Gamma[\alpha+\beta]}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1},](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Probability_Distribution_Calculator/math-e58731e90ded309ff0efc104b9444cbb.png?v=0)
where  is first shape parameter; is first shape parameter; 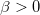 is second shape parameter; and is second shape parameter; and 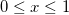 . .
Exponential distribution
The probability density function is
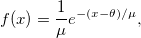
where 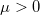 is scale parameter; is scale parameter; 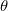 is threshold parameter; and is threshold parameter; and 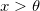 . .
Gamma distribution
The probability density function is
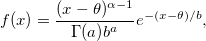
where 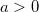 is shape parameter; is shape parameter; 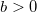 is scale parameter; is scale parameter; 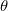 is threshold parameter; and is threshold parameter; and 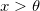 . .
Weibull distribution
The probability density function is
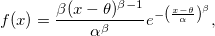
where  is scale parameter; is scale parameter; 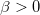 is shape parameter; is shape parameter; 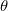 is threshold parameter; and is threshold parameter; and 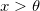 . .
Uniform distribution
The probability density function is
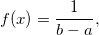
where  is lower endpoint; is lower endpoint; 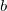 is upper endpoint; and is upper endpoint; and 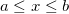 . .
Binomial distribution
The probability density function is
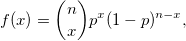
where  is number of trials; is number of trials; 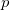 is event probability; and is event probability; and 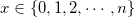 . .
Poisson distribution
The probability density function is
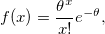
where 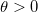 is mean; and is mean; and 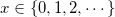 .
link title .
link title
|