2.6 Plant Physiology Fitting FunctionsPlant-Physiology-Fitting-Functions
This opx, Plant Physiology Fitting Functions will add five fitting functions for plant physiology to Origin automatically.
BoxLucas1ModP3
Function
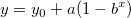
Brief Description
a parameterization of Box Lucas Model with 3 parameters
Sample Curve
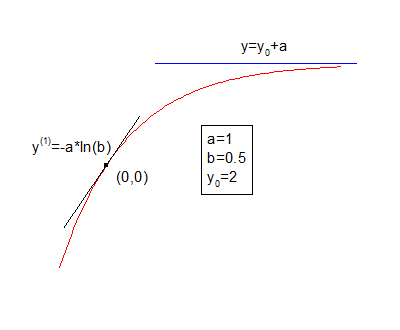
Parameters
Number: 3
Names: a, b, y0
Meanings: a = amplitude, b = base, y0 = offset
Lower Bounds: none
Upper Bounds: none
Script Access
nlf_BoxLucas1ModP3(x,a,b,y0)
Function File
fitfunc\BoxLucas1ModP3.fdf
Category
Exponential
BoxLucas1P3
Function
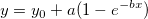
Brief Description
Box Lucas Model with 3 parameters
Sample Curve
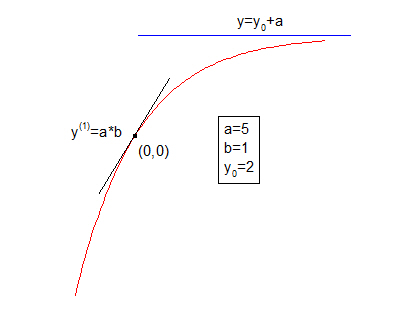
Parameters
Number: 3
Names: a, b, y0
Meanings: a = amplitude, b = rate constant, y0 = offset
Lower Bounds: none
Upper Bounds: none
Script Access
nlf_BoxLucas1P3(x,a,b,y0)
Function File
fitfunc\BoxLucas1P3.fdf
Category
Exponential
ExpDec2Mod
Function
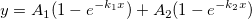
Brief Description
Double, four-parameter exponential decay function.
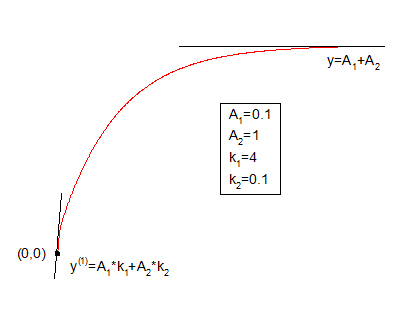
Sample Curve
Parameters
Number: 4
Names: A1, k1, A2, k2
Meanings: A1 = amplitude, k1 = rate constant, A2 = amplitude, k2 = rate constant
Lower Bounds: 0<k1,k2
Upper Bounds: none
Derived Parameters
Individual decay constant:
t1=1/k1
t2=1/k2
Script Access
nlf_ExpDec2Mod(x,A1,A2,k1,k2)
Function File
fitfunc\ExpDec2Mod.fdf
Category
Exponential
NonRectHyperbola
Function
![y=\frac{1}{2\theta}\left[ {\alpha}x+y_m-\sqrt{({\alpha}x+y_m)^2-4{\alpha}{\theta}y_mx } \right]-y_0 y=\frac{1}{2\theta}\left[ {\alpha}x+y_m-\sqrt{({\alpha}x+y_m)^2-4{\alpha}{\theta}y_mx } \right]-y_0](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Plant_Physiology_Fitting_Functions/math-f7843cfcfa0b52db254f96812a42f5e0.png?v=0)
Brief Description
Non-rectangular hyperbola
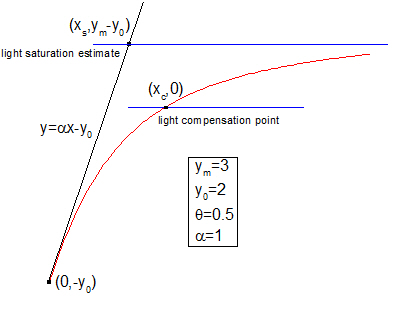
Sample Curve
Parameters
Number: 4
Names:  , , 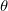 , , 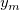 , , 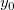
Meanings:  = initial slope, = initial slope, 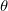 = convexity factor, = convexity factor, 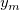 = asymptotic value, = asymptotic value, 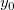 = offset = offset
Lower Bounds: 0 < 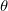
Upper Bounds: 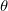 < 1 < 1
Derived Parameters
light compensation point 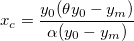
light saturation estimate 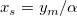
Script Access
nlf_NonRectHyperbola(x,theta,alpha,ym,y0)
Function File
fitfunc\NonRectHyperbola.fdf
Category
Hyperbola
RLC
Function
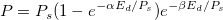
Brief Description
Rapid light curve fitting model
Sample Curve
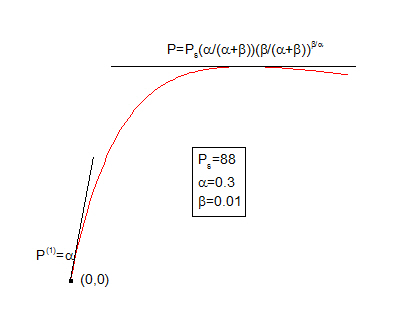
Parameters
Number: 3
Names: 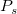 , ,  , , 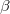
Meanings: 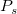 = Scale Factor, = Scale Factor,  = Initial Slope, = Initial Slope, 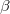 = RLC Slope = RLC Slope
Lower Bounds: 0 <=  , , 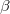
Upper Bounds: none
Derived Parameters
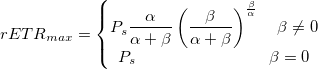
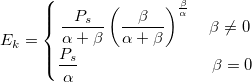
Script Access
nlf_RLC(Ed,Ps,alpha,beta)
Function File
fitfunc\RLC.fdf
Category
Plant Physiology
|