2.29.2 Algorithm for Gage R&R StudyAlgorithm-GG
Type 1 Gage Study
Basic Statistics
- Mean
-
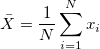
- StdDev
-
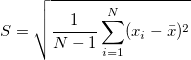
- Study Variation(SV)
-
 , where , where 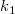 is the number of SD specified in the dialog. Default is 6. is the number of SD specified in the dialog. Default is 6.
- Tolerance
- Tolerance = USL – LSL specified in the dialog.
- % of Tol: Calculate whether the gage resolution (specified in the dialog) is less than(good), greater(bad), or equal to 5% of the tolerance.
Bias
- Bias
-
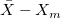 , where , where 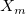 is the reference mean value specified in the dialog. is the reference mean value specified in the dialog.
- T
- t-statistics to test the null hypothesis
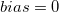 vs alternative hypothesis vs alternative hypothesis 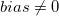 : :
-

Capability
- Cg
- The capability of the gage:
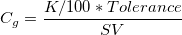 , where , where  is the percent of the tolerance for calculating is the percent of the tolerance for calculating 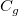 which is specified in the dialog. which is specified in the dialog.
- Cgk
- The capability of the gage, considering both the gage variation and the bias:
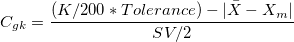
- %Var (Repeatability)
- Compare the gage repeatability with the tolerance:
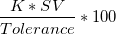
- %Var (Repeatability and Bias)
- Compare the gage repeatability and bias with the tolerance:
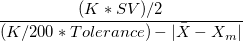
Gage Linear Bias Analysis
Utilize the Bias versus Reference Value plot to observe the variation in bias values 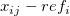 for each part. Subsequently, apply linear regression to the Bias versus Reference Value plot to estimate the slope and intercept. for each part. Subsequently, apply linear regression to the Bias versus Reference Value plot to estimate the slope and intercept.
Gage Linearity
- S
-
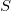 estimates the standard deviation around the regression line. estimates the standard deviation around the regression line.  , where , where 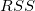 is the residual sum of squares and is the residual sum of squares and 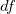 is the degree freedom of the error terms of the linear regression. is the degree freedom of the error terms of the linear regression.
- Linearity
- Linearity assesses whether the gage maintains consistent accuracy across all sizes of objects being measured.
-
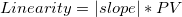 , where , where 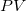 is is 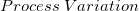 which represents 6 * the process standard deviation and is specified in the dialog if user has it. which represents 6 * the process standard deviation and is specified in the dialog if user has it.
- %Linearity
- %Linearity represents linearity as a percentage of the process variation.
-
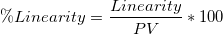
Gage Bias
- Bias
- Bias refers to the disparity between the part's reference value and the measurements taken by the operator.
-
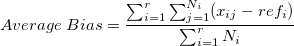
- where
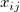 is the is the 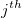 measurement of the measurement of the 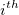 part, part, 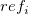 is the reference value of the is the reference value of the 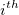 part, part, 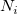 is the number of replicates of the is the number of replicates of the 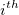 part, part,  is the number of parts. is the number of parts.
- %Bias
- %Bias represents bias as a percentage of the process variation.
-
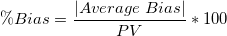
Methods to estimate repeatability standard deviation
- Use the p-values to test whether the bias is 0 at each reference value, and whether the average bias is 0.
- sample range method
- If each reference value corresponds to a unique part,
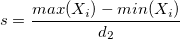 . .
- If more than one part has the same reference value,
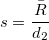 , where , where 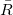 is the average range of the bias of each part and is the average range of the bias of each part and ![d_2 = d_2^*[m_i, i] d_2 = d_2^*[m_i, i]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_GG/math-ce14b7f39fed905b076a31778737229e.png?v=0) . .
- The t-statistic for testing bias is
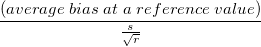 , where , where  is number of parts. is number of parts.
- sample standard deviation method
- If each reference value corresponds to a unique part,
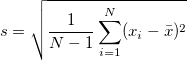 . The t-statistics for testing bias is . The t-statistics for testing bias is 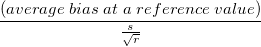 . .
- If more than one part has the same reference value,
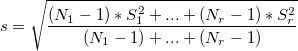 . The t-statistics for testing bias is . The t-statistics for testing bias is 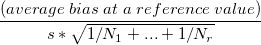 . .
Crossed Gage R&R Study
ANOVA Table
- When you enter Operators and Parts, the data is analyzed with a balanced two-factor factorial design. Both factors are considered to be random. The Operator by Part interaction is included in the model first:
-
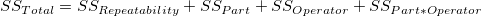
- If the p-value for the interaction is greater than the significance level, the interaction term will be ignored and the data is then fitted with a reduced model with only main terms.
-
 , ,
- where
-
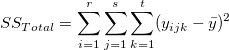
-
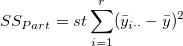
-
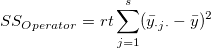
-

- When the interaction term is in the ANOVA model:
-
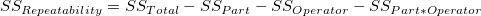
- When the interaction term is not in the ANOVA model:
-
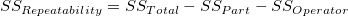
-
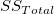 is the total sum of square, is the total sum of square, 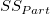 represents the variability of the average differences from factor Part, represents the variability of the average differences from factor Part,  represents the variability of the average differences from factorOperator, represents the variability of the average differences from factorOperator, 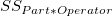 represents the variability of interaction, and represents the variability of interaction, and 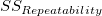 represents the variability of all individual samples. represents the variability of all individual samples.  represents the number of parts. represents the number of parts.  represents the number of operators. represents the number of operators.  represents the number of replicates. represents the number of replicates.
- Two-way ANOVA table with interaction:
| Source of Variation
|
Degrees of Freedom (DF)
|
Sum of Squares (SS)
|
Mean Square (MS)
|
F Value
|
Prob > F
|
| Part
|
r - 1
|
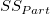
|
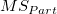
|

|
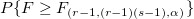
|
| Operator
|
s - 1
|

|
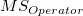
|
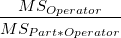
|
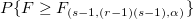
|
| Part*Operator
|
(r- 1) (s - 1)
|
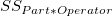
|
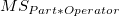
|

|
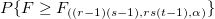
|
| Repeatability
|
rs (t - 1)
|
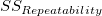
|
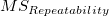
|
|
|
| Total
|
rst - 1
|
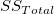
|
|
|
|
- Two-way ANOVA table without interaction:
| Source of Variation
|
Degrees of Freedom (DF)
|
Sum of Squares (SS)
|
Mean Square (MS)
|
F Value
|
Prob > F
|
| Part
|
r - 1
|
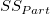
|
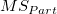
|
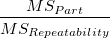
|
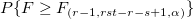
|
| Operator
|
s - 1
|

|
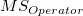
|
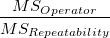
|
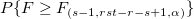
|
| Repeatability
|
rst - r - s + 1
|
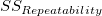
|
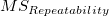
|
|
|
| Total
|
rst - 1
|
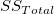
|
|
|
|
Number of Distinct Categories
- The number of distinct categories represents the number of groups that the measurement system can differentiate.
-
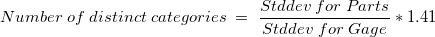
Gge R&R Table
Variance for ANOVA method
The variance components are calculated based on the ANOVA table. The value will be reported as zero if is negative.
Variance for Xbar and R method
- For variance contributed by each source, the standard deviation is calculated as:
-
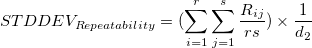
- where
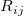 is the range of measurements by operator j for part i. is the range of measurements by operator j for part i. ![d_2 = d_2^*[rs, t] d_2 = d_2^*[rs, t]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_GG/math-c9cea6c72205e7b899dac4b370f5ba7d.png?v=0) . .
-
![STDDEV_{Reproducibility} = \sqrt{\biggr[\bar{X}_{diff}*\frac{1}{d_2}\biggr]^2 - \biggr[\frac{(STDDEV_{repe atability})^2}{rt}\biggr]} STDDEV_{Reproducibility} = \sqrt{\biggr[\bar{X}_{diff}*\frac{1}{d_2}\biggr]^2 - \biggr[\frac{(STDDEV_{repe atability})^2}{rt}\biggr]}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_GG/math-2097f3d11b92a95d4e77ca82b7172fce.png?v=0)
- where
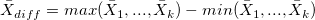 , , ![d_2 = d_2^*[1, s] d_2 = d_2^*[1, s]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_GG/math-abde0a119eb3a64014f6b6e55debbb71.png?v=0)
-
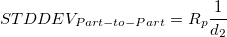
- where
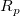 is the range of part average values, is the range of part average values, ![d_2 = d_2^*[1, r] d_2 = d_2^*[1, r]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_GG/math-04e70a9af64720988e508fc2804114fe.png?v=0)
-
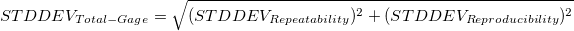
-
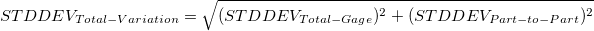
%Contribution

StdDev
If historical standard deviation  is specified and is larger than the gage standard deviation is specified and is larger than the gage standard deviation 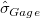 , then the total standard deviation is , then the total standard deviation is  and and 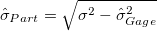 . Otherwise, total standard deviation calculated from the data is used: . Otherwise, total standard deviation calculated from the data is used: 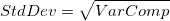
Study Var
The study variation is calculated as the standard deviation for each source of variation multiplied by 6 or the multiplier specified in Study variation.
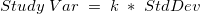
%Study Var
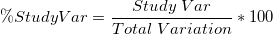
%Tolerance
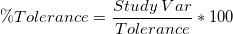 , where , where 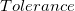 is user entered. is user entered.
%Process
 , where , where 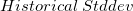 is user entered. is user entered.
Nested Gage R&R Study
ANOVA Table
- Partition of the variation into components for the ANOVA table:
-
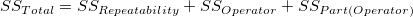
- where
-
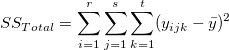
-
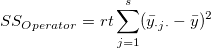
-
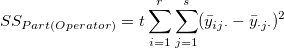
-
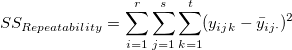
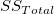 is the total sum of square, is the total sum of square,  represents the variability of the average differences from factorOperator, represents the variability of the average differences from factorOperator, 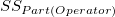 represents the variability of nested factors, and represents the variability of nested factors, and 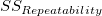 represents the variability of all individual samples. represents the variability of all individual samples.  represents the number of parts. represents the number of parts.  represents the number of operators. represents the number of operators.  represents the number of replicates. represents the number of replicates.
ANOVA table with the nested term:
| Source of Variation
|
Degrees of Freedom (DF)
|
Sum of Squares (SS)
|
Mean Square (MS)
|
F Value
|
Prob > F
|
| Operator
|
s - 1
|

|
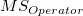
|
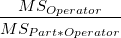
|
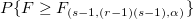
|
| Part(Operator)
|
(r- 1) s
|
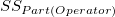
|

|
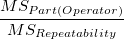
|

|
| Repeatability
|
rs (t - 1)
|
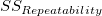
|
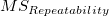
|
|
|
| Total
|
rst - 1
|
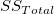
|
|
|
|
Gge R&R Table
- The variance components are calculated based on the ANOVA table. The value will be reported as zero if is negative.
-
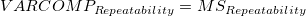
-
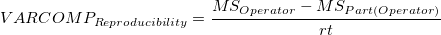
-
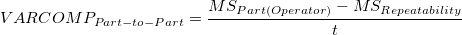
-
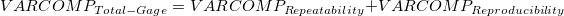
-
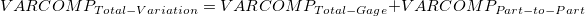
Expanded Gage R&R Study
The app uses the general linear regression model to perform Gage R&R studies with three types of ANOVA models: the random-effects model, the mixed-effects model, and the nested designs model. By default the random-effects model is used. The mixed-effects model is used if any fixed factor is specified. The nested term will be involved if nested term is specified.
The model used for the gage study includes the main effects and the significant highest order interactions and the relevant interactions between. The app uses Fit General Linear Model to generate the ANOVA table and estimate the variance components of the factors and their interactions.
Variance Components for random effects
- Partition of the variation into components for the ANOVA table:
-
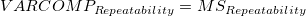
-

-

-
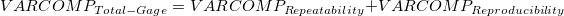
-
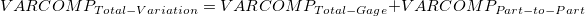
Variance Components for fixed effects
- For fixed terms, the variability across the levels of the term is estimated to represent the variance components. After fitting with general linear model, the fitted coefficients for the first
 levels of the factor are calculated. The coefficient for Jth level is levels of the factor are calculated. The coefficient for Jth level is 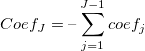 . Then: . Then: 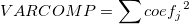 . .
Attribute Gage Study
Bias
- Bias
-
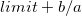 , where , where  is tolerance limit provided by user. is tolerance limit provided by user. 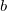 and and  are the intercept and slope from the fitted line on the probability plot. are the intercept and slope from the fitted line on the probability plot.
- Pre-adjusted repeatability
-
 , where , where 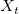 is the estimated reference values at acceptance probabilities of 0.995 and 0.005 on the fitted line. is the estimated reference values at acceptance probabilities of 0.995 and 0.005 on the fitted line.
- Repeatability
-
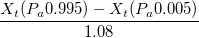
Test of Bias = 0
- AIAG method
- T:

- DF:
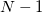 , where , where 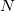 is the number of trials. is the number of trials.
- Regression Method
- T:
 , where , where  is the lower tolerance limit, is the lower tolerance limit,  is the error standard deviation from the fitted line, is the error standard deviation from the fitted line,  is the number of parts, is the number of parts, 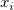 is the reference value of each part, is the reference value of each part,  is the mean of the reference values. is the mean of the reference values.
- DF:
 , where , where 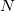 is number of points used for the fitting. is number of points used for the fitting.
Reference
- AIAG MSA-4:2010, Measurement Systems Analysis (MSA), 4th Edition
|