2.2.2.2 Cross Correlation (CCF)CCF
Summary
This CCF (Cross Correlation function) tool is supported in the Time Series Analysis App. It is used to compute and plot the cross correlations between two series.
Tutorial
This tutorial uses App’s built-in sample project. To open this sample OPJU file:
- Right click the Time Series Analysis App icon
 in the Apps Gallery and choose Show Samples Folder. in the Apps Gallery and choose Show Samples Folder.
- A folder will open. Drag-and-drop the project file TSA Sample.opju into Origin.
CCF
- Expand Project Explorer docked on the left. Select folder Statistics and Test . The Book5 contains data
about marketing spending and income .
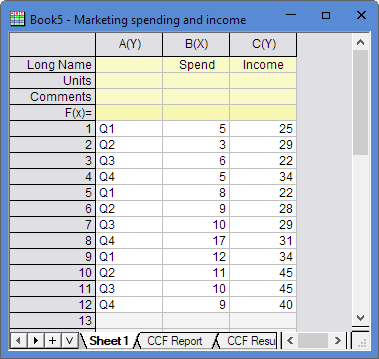
- Highlight Column B and C, and then click the Time Series Analysis App icon
 in the Apps Gallery. in the Apps Gallery.
- In the dialog, select Statistics and Test and CCF tool.
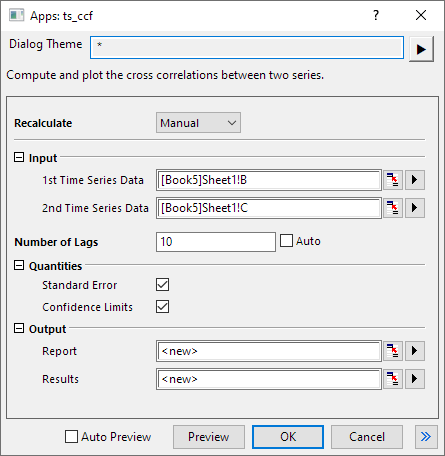
- Set Number of Lags to 10. Then click the OK button.
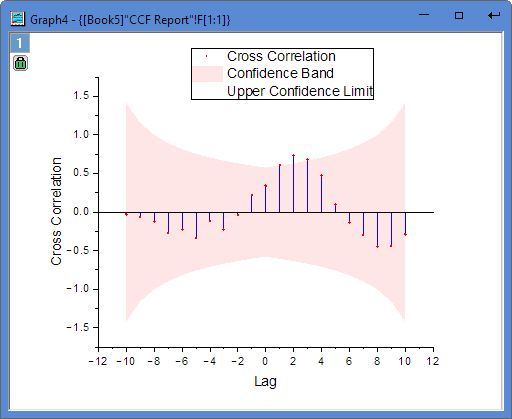
- Then you will get the report with CCF graph.
Algorithm
Cross correlation calculates the correlation between two time series with different lags. It can be used to identify lags of one time series so that it can be the predictor of the other time series.
This app calls nag_tsa_cross_corr (g13bcc) function [1] to calculate.
Given two time series xi, yi, i = 1, 2, ..., n, the cross correlations between xt and yt with lags can be calculated as:
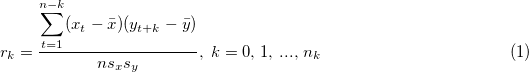
where 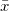 and and 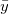 are means of time series xi and yi, sx and sy are standard deviations of time series xi and yi, are means of time series xi and yi, sx and sy are standard deviations of time series xi and yi,
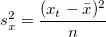
and similarly for sy.
For lag k<0, it can be calculated by exchange time series xi and yi in Equation (1).
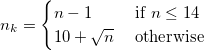
- Standard Error of Cross Correlation
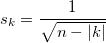
Lower confidence limit at lag k:
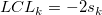
Upper confidence limit at lag k:
Reference
1. nag_tsa_cross_corr (g13bcc)
|