2.2.5.1.2 Algorithm for ARIMATSA-ARIMA-Algorithm
ARIMA model means an autoregressive integrated moving average model. And it may include autoregressive(AR), moving average (MA) or differencing. In this app, nag function nag_tsa_multi_inp_model_estim (g13bec) is used to fit an ARIMA model [1], and nag function nag_tsa_multi_inp_model_forecast (g13bjc) is used to forecast future values by a known ARIMA model [2].
ARIMA Model
For a general ARIMA model,
,
where 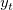 is the input time series (t = 1 ... n), P, Q, D, p, q, d are orders of seasonal autoregressive, seasonal moving average, seasonal differencing, autoregressive, moving average and differencing respectively. And s is the seasonal period. c is the mean of the differenced values, is the input time series (t = 1 ... n), P, Q, D, p, q, d are orders of seasonal autoregressive, seasonal moving average, seasonal differencing, autoregressive, moving average and differencing respectively. And s is the seasonal period. c is the mean of the differenced values,  , , 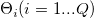 , , 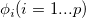 , , 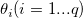 are coefficients for seasonal autoregressive, seasonal moving average, autoregressive and moving average. are coefficients for seasonal autoregressive, seasonal moving average, autoregressive and moving average.  is the residual. is the residual.
Estimation
Residual series  can be obtained by can be obtained by 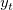 in equation 1. Sum squares of residuals: in equation 1. Sum squares of residuals:
Estimation Criterion
Three criteria are available:

Iterate by minimizing D.
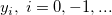 are considered as unobserved random variables with known distribution. are considered as unobserved random variables with known distribution.

where the multiplier M is a function calculated from the ARIMA model arguments.
Minimizing D is equivalent to maximizing the exact likelihood of the data.

but with a different value of M. It is distinct from exact likelihood method only if the mean term is included in the model.
In this app, Marquardt method [4] is used to minimize the objective function.
Quantities
- Residual

Residuals are available at 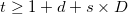 . .
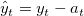
- Residual Degrees of Freedom
Differenced series length is: 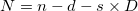 , and , and 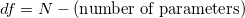 . .
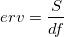
- Covariance Matrix of Parameters
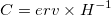
where H is the linearised least squares matrix in the final iteration.
Forecast
To predict time series 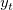 at t = n + 1, ... n + L, set at t = n + 1, ... n + L, set 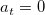 for t = n + 1, ... n + L, and calculate the predicted value by reversing Eq 1. for t = n + 1, ... n + L, and calculate the predicted value by reversing Eq 1.
The forecast error variance of 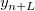 can be calculated as: can be calculated as:
where Vn is the residual variance of the ARIMA model, and 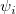 is the "psi-weights" of the model as defined in [3]. is the "psi-weights" of the model as defined in [3].
Reference
- nag_tsa_multi_inp_model_estim (g13bec)
- nag_tsa_multi_inp_model_forecast (g13bjc)
- George E. P. Box and Gwilym M. Jenkins (1976). Time Series Analysis: Forecasting and Control. (Revised Edition) Holden–Day
- D. W. Marquardt (1963). "An algorithm for least squares estimation of nonlinear parameters". J. Soc. Indust. Appl. Math. 11 431.
|