2.75.5.2 Algorithm for Control ChartsAlgorithm-Control-Charts
Tests for Special Causes
- Test 1: One Point More Than 3
 From Center Line From Center Line
- Test if the point (subgroup) is out of the center line more than 3
 . .
- Test 2: Nine Points in a Row on The Same Side of The Center Line
- Test if there are nine consecutive points (subgroups) on the same side (all above or all below) the center line.
- Test 3: Six Points in a Row, All Increasing or All Decreasing
- Test if there are six consecutive points (subgroups) strictly monotonous.
- Test 4: Fourteen Points in a Row, Alternating Up and Down
- Test if there are fourteen consecutive points (subgroups) alternating up and down, that is one point is bigger than the previous point, and then the next point is smaller this one, alternately.
- Test 5: Two Out of Three Points More Than 2
 From The Center Line (Same Side) From The Center Line (Same Side)
- Test if in 3 consecutive points (subgroups), there are 2 points out of the center line more than 2
 on the same side, that is all points are above or below the center line. on the same side, that is all points are above or below the center line.
- Test 6: Four Out of Five Points More Than 1
 From Center Line (Same Side) From Center Line (Same Side)
- Test if in 5 consecutive points (subgroups), there are 4 points out of the center line more than 1
 on the same side, that is all points are above or below the center line. on the same side, that is all points are above or below the center line.
- Test 7: Fifteen Points in a Row Within 1
 of Center Line (Either Side) of Center Line (Either Side)
- Test if there are 15 consecutive points (subgroups) within 1
 of the center line, that is, the ranges of all points to the center line are less than 1 of the center line, that is, the ranges of all points to the center line are less than 1  . .
- Test 8: Eight Points in a Row More Than 1
 From Center Line (Either Side) From Center Line (Either Side)
- Test if there are 8 consecutive points (subgroups) out of the center line more than 1
 , that is, the ranges of all points to the center line are more than 1 , that is, the ranges of all points to the center line are more than 1  . .
Variables Charts for Subgroups
Charts include Xbar-R, Xbar-S, I-MR-R/S (Between/Within), Xbar, R, S, and Zone charts.
Xbar-R
- Sigma Estimation: If the historical value is specified, this historical value is used, otherwise, estimated from data.
- Xbar Chart
- Plotted Points: The mean of the observations for each subgroup.
-

- where
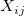 is the is the 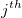 observation in the observation in the  subgroup, and subgroup, and  is the number of observations in subgroup is the number of observations in subgroup  . .
- Center Line: Represents the process mean, the historical value is used if specified, otherwise, uses the mean of data calculated as follows:
-
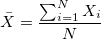 , where , where 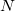 is the total number of observations. is the total number of observations.
- Control Limits
- For each subgroup
 , lower control limit (LCL) is calculated by , lower control limit (LCL) is calculated by 
- For each subgroup
 , upper control limit (UCL) is calculated by , upper control limit (UCL) is calculated by 
- where
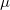 is the process mean, is the process mean, 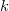 is the parameter for Test 1, is the parameter for Test 1,  is the process standard deviation, and is the process standard deviation, and  is the number of observations in subgroup is the number of observations in subgroup  . .
- R Chart
- Plotted Points: The range for each subgroup.
-

- Center Line
-
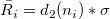 , where , where  is the number of observations in subgroup is the number of observations in subgroup  , , 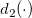 is the value of unbiasing constant is the value of unbiasing constant 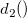 , and , and  is the process standard deviation. is the process standard deviation.
- Control Limits
- For each subgroup
 , lower control limit (LCL) is calculated by , lower control limit (LCL) is calculated by 
- For each subgroup
 , upper control limit (UCL) is calculated by , upper control limit (UCL) is calculated by 
- where
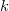 is the parameter for Test 1, is the parameter for Test 1,  is the process standard deviation, is the process standard deviation,  is the number of observations in subgroup is the number of observations in subgroup  , , 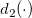 is the value of unbiasing constant is the value of unbiasing constant 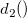 , and , and 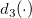 is the value of unbiasing constant is the value of unbiasing constant 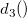 . .
Xbar-S
- Sigma Estimation: If the historical value is specified, this historical value is used, otherwise, estimated from data.
- Sbar: Please refer to Average of Subgroup Standard Deviations (Sbar) in Standard Deviation Estimation section for more details about the formula.
- Pooled Standard Deviation: Please refer to Pooled Standard Deviation in Standard Deviation Estimation section for more details about the formula.
- Xbar Chart: Please refere to Xbar Chart in Xbar-R section above.
- S Chart
- Plotted Points: The standard deviation for each subgroup,
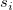 . .
- Center Line
- Not use unabiasing constant:

- Use unabiasing constant:

- where
 is the number of observations in subgroup is the number of observations in subgroup  , , 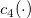 is the value of unbiasing constant is the value of unbiasing constant 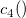 , and , and  is the process standard deviation. is the process standard deviation.
- Control Limits
- For each subgroup
 , lower control limit (LCL) is calculated by: , lower control limit (LCL) is calculated by:
- Not use unabiasing constant:

- Use unabiasing constant:

- For each subgroup
 , upper control limit (UCL) is calculated by: , upper control limit (UCL) is calculated by:
- Not use unabiasing constant:

- Use unabiasing constant:

- where
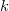 is the parameter for Test 1, is the parameter for Test 1,  is the process standard deviation, is the process standard deviation,  is the number of observations in subgroup is the number of observations in subgroup  , , 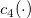 is the value of unbiasing constant is the value of unbiasing constant 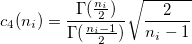 , and , and 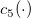 is the value of unbiasing constant is the value of unbiasing constant 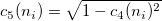 . .
I-MR-R/S (Between/Within)
- Sigma Estimation: Please refer to Standard Deviation Estimation for the details. And please note, if the historical between standard deviation is specified,
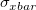 is calculated by: is calculated by:
-

- I Chart
- Plotted Points: For each data point, plot the mean of each subgroup.
- Center Line: The process mean,
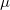 . If a historical value is specified, use this historical value, otherwise, estimate the mean of the data. . If a historical value is specified, use this historical value, otherwise, estimate the mean of the data.
- Control Limits
- Lower control limit (LCL) is calculated by

- Upper control limit (UCL) is calculated by

- where
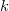 is the parameter for Test 1, is the parameter for Test 1,  is the process standard deviation, and is the process standard deviation, and 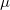 is the process mean. is the process mean.
- MR Chart
- Plotted Points: For each data point, plot the moving range (
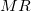 ) of the means of subgroups. ) of the means of subgroups.
- Center Line: Estimate the unbiased average of the moving range by:
-

- where
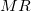 is moving range of the means of subgroups, is moving range of the means of subgroups, 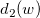 is the unbiasing constant, and is the unbiasing constant, and 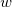 is the number of points in the moving range. is the number of points in the moving range.
- Control Limits
- Lower control limit (LCL) is calculated by

- Upper control limit (UCL) is calculated by

- where
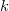 is the parameter for Test 1, is the parameter for Test 1,  is the process standard deviation, is the process standard deviation, 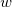 is the number of points in the moving range, is the number of points in the moving range, 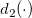 is the value of unbiasing constant is the value of unbiasing constant 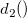 , and , and 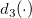 is the value of unbiasing constant is the value of unbiasing constant 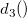 . .
- R Chart: Please refer to R Chart in Xbar-R section above.
- S Chart: Please refer to S Chart in Xbar-S section above.
Xbar
Please refer to Xbar Chart in Xbar-R section above.
R
Please refer to R Chart in Xbar-R section above.
S
Please refer to S Chart in Xbar-S section above.
Zone
- Sigma Estimation: Please refer to Standard Deviation Estimation section for more details about the formula.
- Plotted Points: Cumulative scores based on zones at 1, 2, and 3 standard deviations from center line. For the first point, it is plotted zone score or weight of
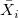 , and then the subsequent plotted point is sum of sequential weights. If the point crosses the center line, the sum is reset to 0. , and then the subsequent plotted point is sum of sequential weights. If the point crosses the center line, the sum is reset to 0.
- Center Line: Overall average of the individual observations or subgroup means.
- Zone Score: There are 4 zones, and different zone has different weight.
- Zone 1: Between center line and
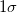 , weight of 0 , weight of 0
- Zone 2: Between
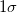 and and 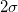 , weight of 2 , weight of 2
- Zone 3: Between
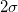 and and 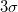 , weight of 4 , weight of 4
- Zone 4: Beyond
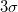 , weight of 8 , weight of 8
Variables Charts for Individuals
Charts include I-MR, Z-MR, Individuals, and Moving Range charts.
I-MR
- Please refer to I Chart and MR Chart in I-MR-R/S(Between/Within) section above.
Z-MR
- Sigma Estimation: Please refer to Standard Deviation Estimation section for more details about the formula. And there are 4 methods for estimating
 : :
- By Runs:
 is estimated for each run independently. is estimated for each run independently.
- By Parts (Combine All Observations for Same Part): All runs data of the same part are used to estimate
 . .
- Constant (Combine All Observations): All the data across runs and parts are used for
 estimation. estimation.
- Relative to Size (Combine All Observations, Use ln): First transform the data by natural log, and then use the transformed data across all runs and all parts for
 estimation. estimation.
- Process Mean: For different part, process mean is calculated separately. Historical values can be specified as process means too.
- Z Chart
- Plotted Points: Plot Z Chart by the data point calculated as follows:
-

- where
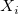 is observation, is observation, 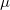 is mean of group, is mean of group,  is the standard deviation of group, and is the standard deviation of group, and 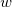 is the width of moving range. is the width of moving range.
- Center Line: It is always 0 because the data are standardized already.
- Control Limits: Because of the standarization of data, lower and upper control limits are always -3 and 3 respectively.
- MR Chart
- Plotted Points: Plot the moving range of the
 values in each group. values in each group.
- Center Line: It is always 1.128 because the data are standardized already.
- Control Limits: Because of the standarization of data, lower control limit is always 0. And upper control limit is different for different estimation method. For average moving range, upper control limit is always 3.686, and for median moving range, it is 3.12.
Individuals
- Please refer to I Chart in I-MR-R/S(Between/Within) section above.
Moving Range
- Please refer to MR Chart in I-MR-R/S(Between/Within) section above.
Attributes Charts
Charts include P Chart Diagnostic, P, Laney P', NP, U Chart Diagnostic, U, Laney U', and C charts.
P Chart Diagnostic
- Plotted Points
- X Data
- Adjusted Counts: First of all, compute the adjusted defective counts (
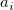 ) as follows: ) as follows:
-
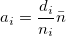 , where , where 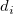 is the count of defectives for subgroup is the count of defectives for subgroup  , ,  is the size of subgroup is the size of subgroup  , and , and 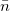 is the mean of subgroup size. is the mean of subgroup size.
- Transformed Counts: Then transform the adjusted counts using the formula below to get the X data:
-

- Y Data
- Four methods aer provided for Y data calculation, including Median Rank (Benard), Mean Rank (Herd-Johnson), Modified Kaplan-Meier, and Kaplan-Meier. And formulas for these for methods are:
-

- where
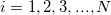 , and , and 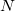 is the number of data points. is the number of data points.
- Y Data Types: There are three data types for Y data available, including Percent, Probability, and Normal Score. The function calculation above for Y data is the Probability, and Percent and Normal Score are computed as:
-

-
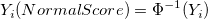 , where , where 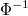 is the inverse standard normal distitribution function. is the inverse standard normal distitribution function.
- Ratio of Observed Variation to Expected Variation
- Expected Variation
-
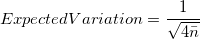 , where , where 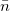 is the mean of subgroup size. is the mean of subgroup size.
- Observed Variation
- First of all, calcuate the normal scores of transformed counts (see
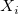 above). Note, this normal score is different from the one for Y data above. Here is the procedure: above). Note, this normal score is different from the one for Y data above. Here is the procedure:
- From the first point of transformed counts to the last point, find out each subsequence points, which are all the same value. For each subsequence, compute normal scores by:
-
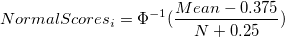 , where , where  is the is the  data point, data point, 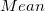 is the mean of the corresponding subsequence, and is the mean of the corresponding subsequence, and 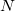 is the total number of data points. is the total number of data points.
- Then get the middle 50% (excluding those less than the 25th percentile or greater than the 75th percentile) of the
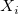 data for use, along with the corresponding data for use, along with the corresponding 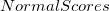 , and then perform the linear fit by the following equation: , and then perform the linear fit by the following equation:
-
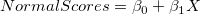 , then get observed variation: , then get observed variation:
-

- Ratio
-

- 95% Confidence Limits for Ratio
-

- where
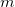 is the number of subgroups, is the number of subgroups, 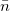 is the mean of subgroup size, is the mean of subgroup size, 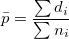 , , 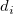 is the count of defectives for subgroup is the count of defectives for subgroup  , ,  is the size of subgroup is the size of subgroup  . .
-
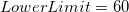 , that is to fix the lower confidence limit for the ratio to 60%. , that is to fix the lower confidence limit for the ratio to 60%.
- Decision
- Compare the ratio to the 95% upper/lower confidence limit.
- Ratio > Upper Confidence Limit: Traditional P chart may result in an elevated false alarm rate, and Laney P' chart is recommended.
- Ratio < Lower Confidence Limit: Traditional P chart may result in control limits that are too wide and Laney P' chart is recommended.
P
- Plotted Points
-
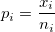 , where , where 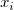 is the number of defectives for subgroup is the number of defectives for subgroup  , and , and  is the size of subgroup is the size of subgroup  . .
- Center Line
- If a historical value is specified, use this historical value, otherwise, use the mean proportion of defectives from data, calculated by:
-
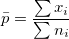 , where , where 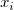 is the number of defectives for subgroup is the number of defectives for subgroup  , and , and  is the size of subgroup is the size of subgroup  . .
- Control Limits
-

-

- where
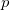 is the process proportion, is the process proportion, 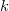 is the parameter for Test 1, and is the parameter for Test 1, and  is the size of subgroup is the size of subgroup  . .
Laney P'
- Plotted Points: The proportion of defectives for each subgroup:
-
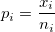 , where , where 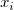 is the number of defectives for subgroup is the number of defectives for subgroup  , and , and  is the size of subgroup is the size of subgroup  . .
- Center Line
- If a historical value is specified, use this historical value, otherwise, use the mean proportion of defectives from data, calculated by:
-
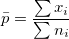 , where , where 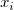 is the number of defectives for subgroup is the number of defectives for subgroup  , and , and  is the size of subgroup is the size of subgroup  . .
- Sigma Z
- Firstly, convert each subgroup proportion
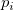 to z-score: to z-score: 
- Then, apply moving range of length 2 to z-score, and get sigma Z as:
-

- where
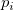 is proportion of defectives for subgroup is proportion of defectives for subgroup  , , 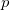 is the process proportion, is the process proportion,  is the size subgroup is the size subgroup  , and , and 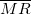 is the moving range of length 2. is the moving range of length 2.
- Control Limits
-

-

- where
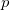 is the process proportion, is the process proportion, 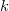 is the parameter for Test 1, is the parameter for Test 1,  is the size of subgroup is the size of subgroup  , and , and 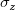 is the Sigma Z calculated above. is the Sigma Z calculated above.
NP
- Plotted Points: The number of defectives in each subgroup (
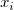 ) is plotted. ) is plotted.
- Center Line
- If a historical value is specified, use this historical value, otherwise, use the mean proportion of defectives from data, calculated by:
-
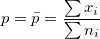 , where , where 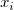 is the number of defectives for subgroup is the number of defectives for subgroup  , and , and  is the size of subgroup is the size of subgroup  . .
- Then center line for each subgroup is computed as follows:
-

- Control Limits
-

-

- where
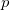 is the process proportion, is the process proportion, 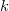 is the parameter for Test 1, and is the parameter for Test 1, and  is the size of subgroup is the size of subgroup  . .
U Chart Diagnostic
- Please refer to P Chart Diagnostic section above for the similar procedure, but with the different calculations summaried below:
- Plotted Points
- X Data
- Transformed Counts
-

- Ratio of Observed Variation to Expected Variation
- Expected Variation
-

- 95% Confidence Limits for Ratio
-

- where
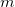 is the number of subgroups, is the number of subgroups, 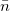 is the mean of subgroup size, is the mean of subgroup size, 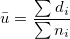 , , 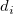 is the defect count for subgroup is the defect count for subgroup  , ,  is the size of subgroup is the size of subgroup  . .
- Decision
- Compare the ratio to the 95% upper/lower confidence limit.
- Ratio > Upper Confidence Limit: Traditional U chart may result in an elevated false alarm rate, and Laney U' chart is recommended.
- Ratio < Lower Confidence Limit: Traditional U chart may result in control limits that are too wide and Laney U' chart is recommended.
U
- Plotted Points: The defect rate for each subgroup:
-
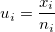 , where , where 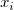 is the number of defects for subgroup is the number of defects for subgroup  , and , and  is the size of subgroup is the size of subgroup  . .
- Center Line
- If a historical value is specified, use this historical value, otherwise, use the mean of the data, calculated by:
-
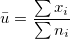 , where , where 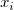 is the number of defectives for subgroup is the number of defectives for subgroup  , and , and  is the size of subgroup is the size of subgroup  . .
- Control Limits
-

-

- where
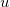 is the process mean, is the process mean, 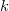 is the parameter for Test 1, and is the parameter for Test 1, and  is the size of subgroup is the size of subgroup  . .
Laney U'
- Plotted Points: The defect rate for each subgroup:
-
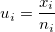 , where , where 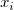 is the number of defects for subgroup is the number of defects for subgroup  , and , and  is the size of subgroup is the size of subgroup  . .
- Center Line
- If a historical value is specified, use this historical value, otherwise, use the mean of the data, calculated by:
-
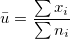 , where , where 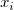 is the number of defectives for subgroup is the number of defectives for subgroup  , and , and  is the size of subgroup is the size of subgroup  . .
- Sigma Z
- Firstly, convert each subgroup rate
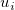 to z-score: to z-score: 
- Then, apply moving range of length 2 to z-score, and get sigma Z as:
-

- where
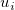 is defect rate for subgroup is defect rate for subgroup  , , 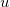 is the process mean, is the process mean,  is the size subgroup is the size subgroup  , and , and 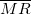 is the moving range of length 2. is the moving range of length 2.
- Control Limits
-

-

- where
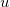 is the process mean, is the process mean, 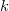 is the parameter for Test 1, is the parameter for Test 1,  is the size of subgroup is the size of subgroup  , and , and 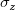 is calculated above. is calculated above.
C
- Plotted Points: The number of defects in each subgroup (
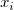 ) is plotted. ) is plotted.
- Center Line
- If a historical value is specified, use this historical value, otherwise, use the process mean is estimated by data:
-
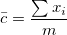 , where , where 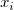 is the number of defects in subgroup is the number of defects in subgroup  , and , and 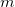 is the number of subgroups. is the number of subgroups.
- Control Limits
-

-

- where
 is the process mean, and is the process mean, and 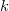 is the parameter for Test 1. is the parameter for Test 1.
Time-Weighted Charts
Charts include Moving Average, EWMA, and CUSUM charts.
Moving Average
- Plotted Points
-

- where
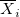 is the mean of the is the mean of the  subgroup, and subgroup, and  is the moving number for average. is the moving number for average.
- Center Line
- If a historical value is specified, use this historical value, otherwise, use the process mean is estimated by data:
-
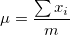 , where , where 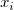 is the observation, and is the observation, and 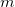 is the number of observations. is the number of observations.
- Control Limits
-

-

- where
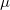 is the process mean, is the process mean, 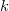 is the parameter for Test 1, is the parameter for Test 1,  is the standard deviation, is the standard deviation,  is the moving number for average, and is the moving number for average, and  is the is the  subgroup size. subgroup size.
EWMA
- Plotted Points
-

- where
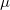 is the process mean, is the process mean, 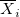 is the mean of the is the mean of the  subgroup, and subgroup, and 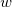 is the weight. is the weight.
- Center Line
- If a historical mean is specified, use this historical mean, otherwise, use the process mean is estimated by data:
-
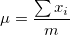 , where , where 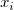 is the observation, and is the observation, and 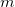 is the number of observations. is the number of observations.
- Control Limits
- The standard deviation of the plotted points is calcuated by:
-

- And then control limits are computed by:
-

-

- where
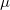 is the process mean, is the process mean, 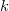 is the parameter for Test 1, is the parameter for Test 1,  is the standard deviation, can be the specified historical value, or calculated from data, is the standard deviation, can be the specified historical value, or calculated from data, 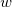 is the weight, and is the weight, and  is the is the  subgroup size. subgroup size.
CUSUM
Tabular CUSUM
- Plotted Points
- The data plotted in a tabular CUSUM chart are
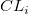 and and 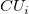 . Normally, they are initialized at 0, but if the process is out of control at startup, FIR (fast initial response) method can be used for initialization, that is . Normally, they are initialized at 0, but if the process is out of control at startup, FIR (fast initial response) method can be used for initialization, that is
-

-

- Then the lower and upper tabular CUSUM plotted points are:
-

-

- where
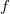 is the number of standard deviation for FIR, is the number of standard deviation for FIR,  is the process standard deviation, is the process standard deviation, is the is the  subgroup size, subgroup size, 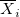 is the mean of the is the mean of the  subgroup, subgroup, 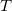 is the target, and is the target, and 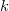 is the size of the shift to detect. is the size of the shift to detect.
- If the previous lower point is smaller than the lower control limit, or the previous upper point is larger than the upper control limit, and you want to reset the signal, then the calculation for
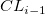 and and 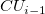 will use will use 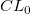 and and 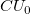 instead respectively. instead respectively.
- Center Line
- The center line is 0.
- Control Limits
-

-

- where
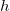 is the decision interval, is the decision interval,  is the process standard deviation, and is the process standard deviation, and  is the is the  subgroup size. subgroup size.
V-mask CUSUM
- Plotted Points
- The data plotted in a V-mask CUSUM chart are
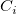 : :
-

- where
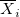 is the mean of the is the mean of the  subgroup, subgroup, 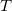 is the target, and is the target, and 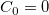 . .
- V-mask Slope
-

- where
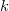 is the slope of the V-mask arm, is the slope of the V-mask arm,  is the process standard deviation, and is the process standard deviation, and  is the is the  subgroup size. subgroup size.
- V-mask Width at Origin
-

- where
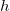 is the decision interval, is the decision interval,  is the process standard deviation, and is the process standard deviation, and  is the is the  subgroup size. subgroup size.
- V-mask Origin
- By default, origin is estimated by number of subgroups.
Multivariate Charts
Charts include T^2-Generalized Variance, T^2, Generalized Variance and Multivariate EWMA charts.
T^2-Generalized Variance
Please refer to T^2 and Generalized Variance Charts in the following T^2 and Generalized Variance sections respectively.
T^2
There are 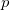 variables, and variables, and  subgroups (or subgroups (or  individual observations). Denote individual observations). Denote  as the mean of the as the mean of the  subgroup (individual observation) for the subgroup (individual observation) for the 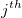 variable, and variable, and  as the mean of subgroup means (individual observations) for the as the mean of subgroup means (individual observations) for the 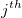 variable. First of all, calculate a variable. First of all, calculate a  matrix as the following: matrix as the following:
-
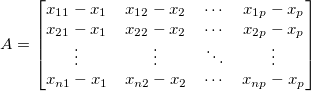
And transposed matrix of  is is  . Sample covariance matrix is . Sample covariance matrix is  , with inversed matrix as , with inversed matrix as  . .  is calculated by: is calculated by:
-
 , where , where  is symmetric matrix by is symmetric matrix by  , and , and  . .
For subgroup data,
- Assume the original data for the
 subgroup of the subgroup of the 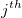 and and  variables are variables are  and and  respectively, where respectively, where  , , 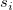 is the size of the is the size of the  subgroup. The covariance between variable subgroup. The covariance between variable  and and 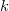 for the for the  subgroup is calculated as: subgroup is calculated as:
-
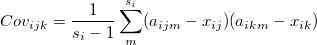
- Then
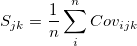
For individual data, there are  individual observations, individual observations,
-
 , where , where  is the difference between two adjacent data for the is the difference between two adjacent data for the 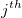 variable, calculated by variable, calculated by  , ,  is the is the  original data in the original data in the 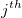 variable. variable.
-
- Calculate matrix
 , and get diagonal values from this matrix as , and get diagonal values from this matrix as  , and then the , and then the  plotted point is plotted point is
-
 , where , where 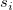 is the size of the is the size of the  subgroup (for individual observation, it is 1). subgroup (for individual observation, it is 1).
-
- The center line for
 chart is calculated by chart is calculated by  . .  and and  are calculated using different formulas for different data types and different covariance matrix sources. There are are calculated using different formulas for different data types and different covariance matrix sources. There are 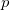 variables, variables,  subgroups (observations), and subgroups (observations), and 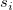 is the size of the is the size of the  subgroup. subgroup.  is the inverse cumulative is the inverse cumulative  distribution. distribution.  is the inverse cumulative is the inverse cumulative  distribution. distribution.
- Covariance matrix is specified
-
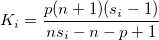
-
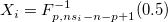
- Covariance matrix is estimated
-
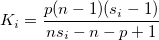
-
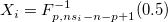
- Covariance matrix is specified
-
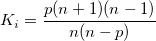
-
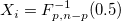
- Covariance matrix is estimated
-
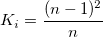
-
 , where , where ![Q = \frac{1}{2}\left[\frac{2(n-1)^2}{3n-4}-p-1\right] Q = \frac{1}{2}\left[\frac{2(n-1)^2}{3n-4}-p-1\right]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_Control_Charts/math-401fa1077311b0414a423eb24b128ca6.png?v=0)
-
- Upper control limit (UCL) is calculated using different formulas for different data types and different covariance matrix sources. There are
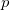 variables, variables,  subgroups (observations for individual data), and subgroups (observations for individual data), and 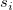 is the size of the is the size of the  subgroup. subgroup.  is the inverse cumulative is the inverse cumulative  distribution. distribution.  is the inverse cumulative is the inverse cumulative  distribution. distribution.  . .
- Covariance matrix is specified
-
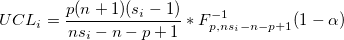
- Covariance matrix is estimated
-
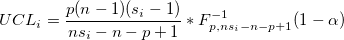
- Covariance matrix is specified
-
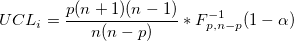
- Covariance matrix is estimated
-
 , where , where ![Q = \frac{1}{2}\left[\frac{2(n-1)^2}{3n-4}-p-1\right] Q = \frac{1}{2}\left[\frac{2(n-1)^2}{3n-4}-p-1\right]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_Control_Charts/math-401fa1077311b0414a423eb24b128ca6.png?v=0)
-
- There are
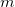 samples (subgroups) out of control points. samples (subgroups) out of control points.
- Calculate unconditional
 values, denote as values, denote as  . .
- For the
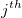 variable, extract the principal submatrix of variable, extract the principal submatrix of  , as , as 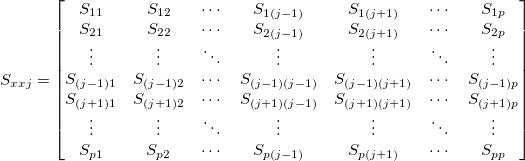
- Denote the inversed matrix of
 as as  . .
- For the
 variable of the variable of the  out of control point, calculate a one-row-matrix: out of control point, calculate a one-row-matrix:
-
 , and denote its transposed matrix as , and denote its transposed matrix as  . .
- Then the unconditional
 value for the value for the  variable of the variable of the  out of control point is out of control point is  , where , where  is the size of subgroup out of control. is the size of subgroup out of control.
- Calculate decomposed
 statistic, denote as statistic, denote as 
-
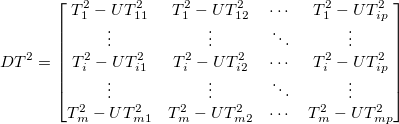
- Calculate
 value of decomposed value of decomposed  . .
-
 is the number of subgroups (observations for individual data). is the number of subgroups (observations for individual data).  is the cumulative distribution function of is the cumulative distribution function of  distribution, and distribution, and  is the cumulative distribution function of is the cumulative distribution function of  distribution. distribution.
- Subgroup Data
- If covariance matrix is specified,
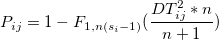
- If covariance matrix is estimated,
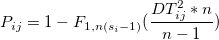
- Individual Data
- If covariance matrix is specified,
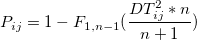
- If covariance matrix is estimated,
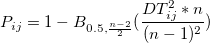
Generalized Variance
There are 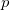 variables, and variables, and  subgroups (or subgroups (or  individual observations). Denote individual observations). Denote  as the mean of the as the mean of the  subgroup (individual observation) for the subgroup (individual observation) for the 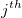 variable, and variable, and  as the mean of subgroup means (individual observations) for the as the mean of subgroup means (individual observations) for the 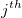 variable. variable.
For subgroup data,
- Assume the original data for the
 subgroup of the subgroup of the 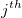 and and  variables are variables are  and and  respectively, where respectively, where  , , 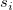 is the size of the is the size of the  subgroup. The covariance between variable subgroup. The covariance between variable  and and 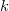 for the for the  subgroup is calculated as: subgroup is calculated as:
-
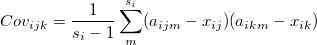
- Then the sample covariance matrix for the
 subgroup is subgroup is
-
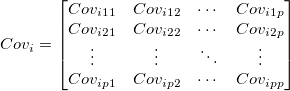
For individual data,
-
 is the sample covariance matrix of all the data, which is calculated by the formula in T^2 section for individual data. is the sample covariance matrix of all the data, which is calculated by the formula in T^2 section for individual data.
-
- For subgroup data, the plotted point is the determinant of the sample covariance matrix,
 . .
- For individual data,
- Normalize the data by
 , where , where  is the is the  observations for the observations for the 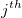 variable, variable,  is the mean of the is the mean of the 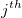 variable, and variable, and  is the is the 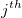 value of diagonal of value of diagonal of  matrix. matrix.
- Plotted point is the square root of variance of each
 observation, that is observation, that is  , where , where 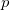 is number of variables, is number of variables,  is the mean of the is the mean of the  observation. observation.
-
- Center line is the determinant of the sample covariance matrix of all the data,
 , where , where  is calculated by the formula in T^2 section for subgroup data. is calculated by the formula in T^2 section for subgroup data.
-
- Center line is the mean of plotted points for individual data.
-
- There are
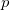 variables, variables,  subgroups (observations for individual data), and subgroups (observations for individual data), and 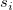 is the size of the is the size of the  subgroup. Lower control limit (LCL) and upper control limit are calculated as following. subgroup. Lower control limit (LCL) and upper control limit are calculated as following.
-
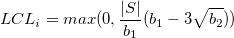
-
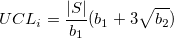
- where
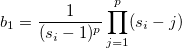
-
![b_2=\frac{1}{(s_i-1)^{2p}}\prod_{j=1}^{p}(s_i-j)\left[\prod_{j=1}^{p}(s_i-j+2)-\prod_{j=1}^{p}(s_i-j)\right] b_2=\frac{1}{(s_i-1)^{2p}}\prod_{j=1}^{p}(s_i-j)\left[\prod_{j=1}^{p}(s_i-j+2)-\prod_{j=1}^{p}(s_i-j)\right]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_Control_Charts/math-23052fe8bce9c8642755102cda36dc50.png?v=0)
-
- Calculate
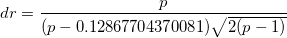
- Calculate
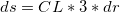
- Then
 , , 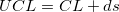
- where
 is the center line value. is the center line value.
Multivariate EWMA
-
- There are
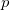 variables, and variables, and  subgroups. Denote subgroups. Denote  as the mean of the as the mean of the  subgroup for the subgroup for the 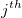 variable, and variable, and  as the mean of subgroup means for the as the mean of subgroup means for the 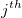 variable. Weight is variable. Weight is 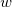 . .  is the sample covariance matrix of all the data, which is calculated by the formula in T^2 section. For the is the sample covariance matrix of all the data, which is calculated by the formula in T^2 section. For the  subgroup, plotted point is computed using the following sequence forumlas. subgroup, plotted point is computed using the following sequence forumlas.
-
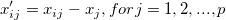
-
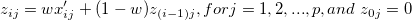
- Form a matrix
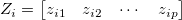
- Weighted covariance matrix
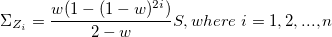
- The
 plotted point is plotted point is 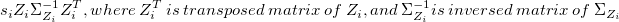
-
- The upper control limit for the MEWMA chart is computed by using the algorithm described in the following literature.
- K M. Bodden and S E. Rigdon (1999). A Program for Approximating the In-Control ARL for the MEWMA Chart. Journal of Quality Technology, 31,January, 120−123.
|