2.75.1.2 Algorithm for Identify Data DistributionAlgorithm-IDD
In this app, MLE (maximum likelihood estimation) method is used to estimate parameters for each distribution except Gaussian Mixture distribution, and the latter uses EM (expectation maximization) algorithm.
In the MLE method, for input data 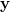 , parameters vector , parameters vector 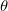 : :
- First calculate the likelihood function
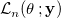 for the distribution, which is the product of probability density functions of input data. for the distribution, which is the product of probability density functions of input data.
- Then maximize the logarithm of the likelihood function
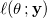 by setting its partial derivatives equal to zero with respect to parameters. by setting its partial derivatives equal to zero with respect to parameters.
- Use Newton-Raphson method to solve these parameters in step 2.
Distributions
In this app, distributions include:
where Φ is the CDF function for the standard normal distribution, and γ is the lower incomplete gamma function.
Note:
- Box-Cox Transformation, Johnson Transformation and Yeo-Johnson Transformation distributions transform data first, and then use Normal distribution to fit. For more, see Algorithm for Data Transformation.
- The scale parameter in Normal and Lognormal distributions is corrected to the unbiased standard deviation, i.e. divided by n-1 instead of n, where n is the number of points.
- The threshold parameter λ in 2-Parameter Exponential distribution is estimated as below:
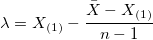 , ,
- where X(1) is the minimum of X, and X is the mean of X.
Goodness of Fit
Anderson-Darling Test
The hypotheses for Anderson-Darling test are:
- H0: Input data follows the distribution.
- H1: Input data doesn't follow the distribution.
- Anderson-Darling Statistic
- Input data is sorted first, and use CDF function to calculate the probability Zi for each point. Anderson-Darling statistic A2 is calculated as below:
- A2 value can be used to assess the fit. The smaller the value is, the better the model will be.
- P-value for Anderson-Darling Test
- P-value is calculated by interpolating the statistic A2 on tables in the reference [1] and [2]. If P-value is less than the critical value, e.g. 0.05, H0 will be rejected.
- For some distributions, no reference is available, their P-values are missing. e.g. 3-Parameter Lognormal distribution.
- For Folded Normal, Gaussian Mixture and 3-Parameter Weibull with fixed shape distributions, P-value is calculated by the Monte Carlo method. 1000 samples are drawn to produce the statistic for the null hypothesized distribution with estimated parameters. The P-value is the proportion of samples whose A2 statistic values are greater than or equal to input data's [4]. i.e.
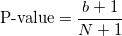 , ,
- where b is the number of statistic values that are greater than or equal to input data's, and N is the number of samples, here N=1000.
BIC
In Gaussian Mixture distribution, BIC value is calculated as follows:
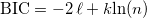 , ,
where ℓ is the logarithm of the likelihood in the estimation, k is the number of parameters, and n is the number of points.
The smaller the BIC value is, the better the model will be.
Likelihood-ratio Test(LRT)
Likelihood-ratio test(LRT) is used to compare two models: a simple model A and a complex model B, and model A is the subset of model B, e.g. model A is Weibull, and model B is 3-Parameter Weibull. It can determine whether the complex model B is significantly better than the simple model A. In this app, likelihood-ratio test supports to compare Lognormal vs 3-Parameter Lognormal, Exponential vs 2-Parameter Exponential, and Weibull vs 3-Parameter Weibull.
The hypotheses for the likelihood-ratio test are:
- H0: The complex model B is the same as the simple model A.
- H1: The complex model B is significantly better than the simple model A.
If P-value for the likelihood-ratio test is less than the critical value, e.g. 0.05, reject H0, and it indicates that the complex model B is significantly better than the simple model A
- Likelihood-ratio test statistic
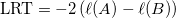 , ,
- where ℓ(A) and ℓ(B) are log likelihoods for the model A and the model B respectively.
- Likelihood-ratio test P-value
Likelihood-ratio test statistic follows Chi-squared distribution with the degrees of freedom df, and df is the difference of number of parameters in the model B and the model A. Thus likelihood-ratio test P-value can be calculated as follows:
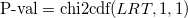 , ,
- where chi2cdf is the upper tail (The third parameter 1 means the upper tail) CDF function for the 𝜒2 distribution.
Estimate Parameter's Standard Error
Once parameters are estimated by MLE method, the Fisher information matrix (FIM) can be calculated by Hessian matrix:
Covariance matrix of parameters can be expressed as:
where n is the number of points.
Parameter's standard error is the square root of the diagonal elements in the covariance matrix C.
Probability Plot
Points in the probability plot are sorted in ascending order, for the ith point, its probability is calculated by the median rank (Benard's method):
The middle line is the expected percentiles for given probabilities in terms of the inverse cumulative distribution function using parameters from the MLE method.
To estimate confidence limits of percentiles, variance of percentiles is calculated by propagation of error:
where xp is the percentile for a given probability p, and (.)T denotes the transpose of a vector.
- Confidence limits of percentiles can be calculated as below:
where 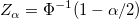 . .
- For some positive random variables, e.g. in Lognormal, Gamma, Exponential, Weibull, Loglogistic, Folded Normal and Rayleigh distributions, confidence limits are:
- For some random variables with a threshold parameter λ, e.g. in 3-Parameter Lognormal, 2-Parameter Exponential and 3-Parameter Weibull distributions, confidence limits are:
- If
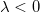 , ,
- If
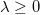 , ,
- If
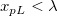 , xpL value will be corrected to λ . , xpL value will be corrected to λ .
- Q-Q plot is shown for Gaussian Mixture distribution. Its expected percentiles are calculated by interpolation.
Reference
- R.A. Lockhart and M.A. Stephens (1994). "Estimation and Tests of Fit for the Three-parameter Weibull Distribution". Journal of the Royal Statistical Society, Vol. 56, No. 3, pp. 491-500.
- Ralph B. D'Agostino, Michael A. Stephens (Eds.) (1986). Goodness-of-Fit Techniques. New York: Marcel Dekker
- Hartigan J A (1975). Clustering Algorithms. Wiley
- W. Stute, W. G. Manteiga, and M. P. Quindimil (1993). “Bootstrap based goodness-of-fit-tests”. Metrika, 40.1: pp. 243-256.
|