2.3.2 Algorithm for Attribute Agreement AnalysisAlgorithm-Attribute-Agreement-Analysis
Assessment Agreement
Percent Agreement
-

where
-
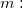 the number of matched ratings. the number of matched ratings.
-
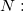 the total number of samples. the total number of samples.
It needs each appraiser rates each sample at least twice. The matched event is that all the trials to the same sample for each appraiser are given the same rating. Otherwise, the rating of that sample for the appraiser is not matched.
- Each Appraiser VS Standard
The standard/attribute for each sample has to be known. The matched event is that all the trials to the same sample for each appraiser are the same with the known standard of this sample. Otherwise, it is not matched.
The matched event is that, to the same sample, all the trials from all appraisers are the same.
- All Appraisers VS Standard
The standard/attribute for each sample has to be known. The matched event is that, to the same sample, all the trials from all appraisers are the same with the known standard of this sample.
Confidence Intervals for Percent Agreement
Given  , the confidence intervals (lower bound and upper bound) for the percent agreement are computed as following (if , the confidence intervals (lower bound and upper bound) for the percent agreement are computed as following (if 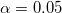 , it is 95% lower bound and upper bound). , it is 95% lower bound and upper bound).
Lower Bound
-

where
-

-

-
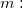 the number of matches. the number of matches.
-
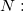 the number of samples. the number of samples.
-
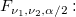 the the 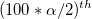 percentile of the F distribution with percentile of the F distribution with 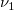 and and 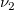 degrees of freedom. degrees of freedom.
If no agreement, that is 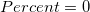 , or , or 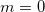 , the lower bound is 0. If perfect agreement, that is , the lower bound is 0. If perfect agreement, that is 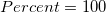 , or , or 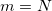 , ,  is used instead of is used instead of 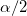 in the formula. in the formula.
Upper Bound
-

where
-

-

-
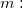 the number of matches. the number of matches.
-
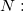 the number of samples. the number of samples.
-
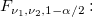 the the 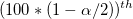 percentile of the F distribution with percentile of the F distribution with 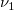 and and 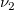 degrees of freedom. degrees of freedom.
If no agreement, that is 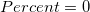 , or , or 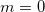 , ,  is used instead of is used instead of 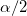 in the formula. If perfect agreement, that is in the formula. If perfect agreement, that is 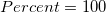 , or , or 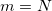 , the upper bound is 1. , the upper bound is 1.
Assessment Disagreement
The assessment disagreement is the difference from the known standard ratings. So, the standard/attribute for each sample has to be known.
Percent Disagreement
-

where
-
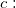 the number of assessments different from the known standard rating. the number of assessments different from the known standard rating.
-
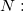 the total number of trials. the total number of trials.
The percent disagreement indicates the percentage of non-matches in the ratings. The non-matched event is that, for each sample, and each appraiser, if the trial is not rating the same with the known standard of that sample. For each non-matched event, the non-matched count increases by 1.
Fleiss' Kappa Statistics
Unknown Standard
There are two cases for computing the Fleiss' kappa statistics with unknown standard, agreement within each appraiser and agreement between all appraisers.
Agreement within each appraiser is to examine the agreement between the trials within each appraiser. so, it needs the number of trials within each appraiser to be greater than 1.
Agreement between all appraisers is interested in the agreement of all the appraisers. So, the number of appraisers is assumed to be greater than 1, and then the number of trials within each appraiser can be 1 or greater than 1.
- Overall Kappa
- The overall kappa coefficient is defined by:
-

- where
-
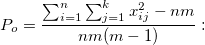 the observed proportion of the pairwise agreement among the trials. the observed proportion of the pairwise agreement among the trials.
-
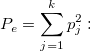 the expected proportion of agreement. the expected proportion of agreement.
-
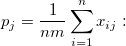 the overall proportion of ratings in category the overall proportion of ratings in category 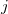 . .
-
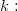 the total number of categories. the total number of categories.
-
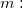 the number of trials. For agreement within each appraiser, it is the number of trials for each appraiser. For agreement between all appraisers, it is the number of trials for all appraisers. the number of trials. For agreement within each appraiser, it is the number of trials for each appraiser. For agreement between all appraisers, it is the number of trials for all appraisers.
-
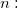 the number of samples. the number of samples.
-
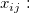 the number of ratings on sample the number of ratings on sample  into category into category 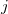 . .
- Kappa for Single Category
- The formula for the kappa coefficient for the
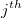 category is defined by: category is defined by:
-

- Each parameter has the same meaning as described above for Overall Kappa.
- Testing Significance
- The following
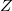 statistic is used to test if statistic is used to test if 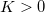 : :
-

- where
-
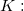 the overall kappa coefficient. the overall kappa coefficient.
-

- Other parameters have the same meanings as described above for Overall Kappa.
- For the
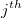 category, the following category, the following 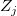 statistic is used for testing if statistic is used for testing if 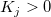 : :
-

- where
-
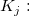 the kappa coefficient for the the kappa coefficient for the 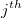 category. category.
-

- Other parameters have the same meanings as described above for Overall Kappa.
Known Standard
- Kappa Statistics
- If the standard is known, the following steps are used for computing kappa coefficients, including overall and single category.
- Consider the standard as one trial, then for each trial, combine with the standard to treat as two trials ratings, and then use the formulas in Unknown Standard to estimate kappa coefficients for these two combined trials.
- Repeat all the trials (assumed there are
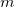 trials) to get the trials) to get the 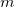 sets of kappa coefficients (including both overall and single category). sets of kappa coefficients (including both overall and single category).
- Calculate the average of the estimated
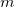 sets of kappa coefficients, and the results are the overall kappa coefficient and single category kappa coefficients respectively. sets of kappa coefficients, and the results are the overall kappa coefficient and single category kappa coefficients respectively.
- Testing Significance
- Follow the same steps as calculation for Kappa Statistics above, and get
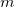 variances of the kappa statistic ( variances of the kappa statistic (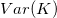 and and 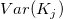 ). ).
- The variance of overall kappa with known standard is then calculated by the sum of the
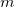 variances, variances, 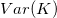 , and divided by , and divided by 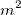 . .
- Similarly, calculate the variance of kappa for a specific category with known standard by the sum of the
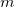 variances for the kappa for a specific category, ( variances for the kappa for a specific category, (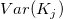 ), and divided by ), and divided by 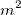 . .
- Finally, use the same formulas in Unknown Standard to calculate the
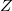 statistic with the obtained variances of overall and singe category in previous steps. statistic with the obtained variances of overall and singe category in previous steps.
Cohen's Kappa Statistics
Unknown Standard
There are two cases to calculate Cohen's kappa statistic with unknown standard, and each case should meet its own condition.
For within appraiser, the condition is that, each appraiser should have exactly two trials for each sample.
For between appraisers, the number of appraisers should be exactly two, and each has only one trial.
Assumed there are 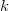 categories, for the ratings from two trials (within appraiser) or two appraisers (one trial for each appraiser), the following table can be used for the calculation. categories, for the ratings from two trials (within appraiser) or two appraisers (one trial for each appraiser), the following table can be used for the calculation.
|
|
Trial 2 (or Appraiser 2)
|
| Trial 1 (or Appraiser 1)
|
1
|
2
|
...
|
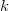
|
Total
|
| 1
|
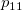
|
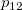
|
...
|
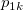
|
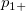
|
| 2
|
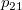
|
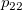
|
...
|
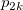
|
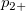
|
| ...
|
...
|
...
|
...
|
...
|
...
|
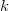
|
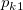
|
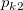
|
...
|
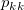
|
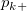
|
| Total
|
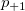
|
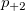
|
...
|
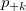
|
1
|
where
-

-
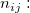 the number of samples that the first trial (appraiser) is rating category the number of samples that the first trial (appraiser) is rating category  , and the second trial (appraiser) is rating category , and the second trial (appraiser) is rating category 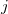 . .
-
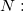 the total number of samples. the total number of samples.
-

-

- Overall Kappa
- The overall kappa coefficient is defined by:
-

- where
-
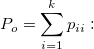 the observed proportion of agreement. the observed proportion of agreement.
-
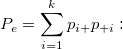 the expected proportion of agreement. the expected proportion of agreement.
- Kappa for Single Category
- The formula for the kappa coefficient for the
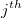 category is calculated by: category is calculated by:
-

- Testing Significance
- The following
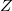 statistic is used to test if statistic is used to test if 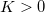 : :
-

- where
-
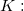 the overall kappa coefficient. the overall kappa coefficient.
-
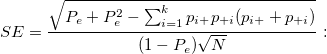 the standard error of kappa coefficient. the standard error of kappa coefficient.
- For the
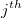 category, the following category, the following 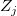 statistic is used for testing if statistic is used for testing if 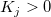 : :
-

- where
-
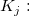 the kappa coefficient for the the kappa coefficient for the 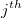 category. category.
-
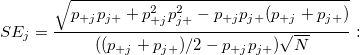 the standard error of kappa coefficient of the the standard error of kappa coefficient of the 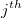 category. category.
Known Standard
To calculate Cohen's kappa statistic with known standard, the similar procedure is used as Unknown Standard.
Assumed there are 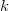 categories for standard, for the ratings from each trial, the following table can be used for the similar calculation. categories for standard, for the ratings from each trial, the following table can be used for the similar calculation.
|
|
Standard
|
| Trial
|
1
|
2
|
...
|
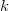
|
Total
|
| 1
|
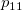
|
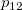
|
...
|
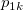
|
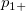
|
| 2
|
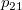
|
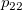
|
...
|
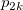
|
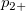
|
| ...
|
...
|
...
|
...
|
...
|
...
|
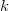
|
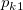
|
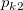
|
...
|
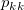
|
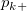
|
| Total
|
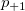
|
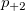
|
...
|
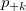
|
1
|
where
-

-
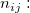 the number of samples that the trial is rating category the number of samples that the trial is rating category  , and the standard is category , and the standard is category 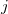 . .
-
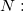 the total number of samples. the total number of samples.
-

-

- Kappa
- Each Appraiser VS Standard
- For the
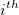 trial, calculate trial, calculate 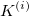 and and 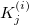 using the same formulas as Unknown Standard. using the same formulas as Unknown Standard.
- Sum up all
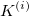 and and 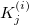 from all trials respectively, and then divided by the number of trials, from all trials respectively, and then divided by the number of trials, 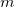 , that is: , that is:
-

-

- All Appraisers VS Standard
- For the
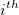 trial from the trial from the 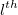 appraiser, calculate appraiser, calculate 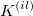 and and 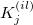 using the same formulas as Unknown Standard. using the same formulas as Unknown Standard.
- Sum up all
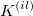 and and 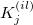 from all trials and all appraisers respectively, and then divided by the number of trials, from all trials and all appraisers respectively, and then divided by the number of trials, 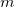 , and the number of appraisers, , and the number of appraisers, 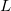 , that is: , that is:
-

-

- Testing Significance
- Each Appraiser VS Standard
- For the
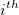 trial, calculate trial, calculate 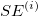 and and 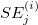 using the same formulas as Unknown Standard. using the same formulas as Unknown Standard.
- Sum up all
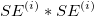 and and 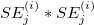 from all trials respectively, and then get the sum of variances. from all trials respectively, and then get the sum of variances.
- The final calculation of
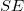 and and 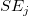 is: is:
-

-

- where
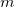 is the number of trials. is the number of trials.
- Then
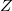 and and 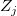 are calculated by: are calculated by:
-
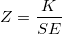 and and 
- All Appraisers VS Standard
- For the
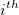 trial from the trial from the 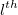 appraiser, calculate appraiser, calculate 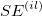 and and 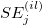 using the same formulas as Unknown Standard. using the same formulas as Unknown Standard.
- Sum up all
 and and 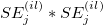 from all trials and all appraisers respectively, and get the sum of variances. from all trials and all appraisers respectively, and get the sum of variances.
- The final calculation of
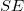 and and 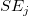 is: is:
-

-

- where
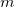 is the number of trials, and is the number of trials, and 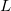 is the number of appraisers. is the number of appraisers.
- Then
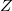 and and 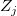 are calculated by: are calculated by:
-
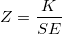 and and 
Kendall's Statistics
To calculate Kendall's statistics, it assumes the ratings and standard are ordinal data, and there are at least 3 or more levels.
If standard is unknown, the Kendall's coefficient of concordance is computed for within appraiser and between appraisers. For within appraiser, there should be at least 2 trials for each appraiser. And for between appraisers, the number of appraisers should be at least 2.
If standard is known, the Kendall's correlation coefficient is computed for each appraiser vs standard and all appraisers vs standard. For all appraisers vs standard, there should be at least 2 appraisers.
Kendall's Coefficient of Concordance
The Kendall's coefficient of concordance is estimated by:
-

where
-
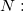 the number of samples. the number of samples.
-
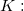 the number of trials for within appraiser. For between appraisers, it is the number of trials for within appraiser. For between appraisers, it is 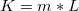 where where 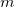 is the number of trials and is the number of trials and 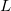 is the number of appraisers. is the number of appraisers.
-
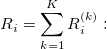 the sum of ranks for the the sum of ranks for the 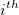 sample, and sample, and 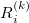 is the rank of each trial from each appraiser for the is the rank of each trial from each appraiser for the 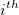 sample. sample.
-
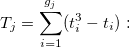 the penalty from the the penalty from the 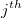 trial. trial.
-
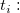 the number of tied ranks in the the number of tied ranks in the 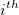 tie (level). tie (level).
-
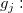 the number of ties (levels) in the the number of ties (levels) in the 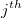 trial. trial.
Testing Significance of Kendall's Coefficient of Concordance
The following formula is used to test the significance of Kendall's coefficient of concordance:
-

where
-
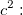 the chi-square distribution with the chi-square distribution with 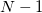 degrees of freedom. degrees of freedom.
-
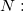 the number of samples. the number of samples.
-
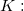 the number of trials for within appraiser. For between appraisers, it is the number of trials for within appraiser. For between appraisers, it is 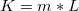 where where 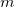 is the number of trials and is the number of trials and 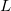 is the number of appraisers. is the number of appraisers.
-
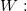 the calculated Kendall's coefficient of concordance. the calculated Kendall's coefficient of concordance.
Kendall's Correlation Coefficient
To calculate Kendall's correlation coefficient between each trial and the standard, the table below is used (assumed there are 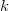 levels). levels).
|
|
Standard
|
| Trial
|
1
|
2
|
...
|
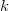
|
Total
|
| 1
|
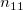
|
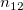
|
...
|
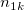
|
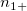
|
| 2
|
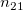
|
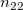
|
...
|
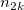
|
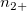
|
| ...
|
...
|
...
|
...
|
...
|
...
|
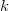
|
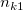
|
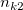
|
...
|
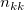
|
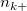
|
| Total
|
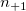
|
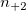
|
...
|
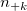
|
N
|
where
-
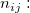 the number of samples that the trial is rating category (level) the number of samples that the trial is rating category (level)  , and the standard is category (level) , and the standard is category (level) 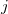 . .
-
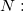 the total number of samples. the total number of samples.
-

-

Then the Kendall's correlation coefficient between each trial and the standard is computed by:
-

where
-
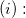 for the for the 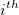 trial from each appraiser. trial from each appraiser.
-
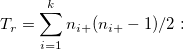 the number of pairs tied on row. the number of pairs tied on row.
-
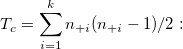 the number of pairs tied on column. the number of pairs tied on column.
-
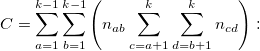 the number of concordant pairs. the number of concordant pairs.
-
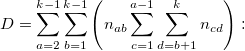 the number of discordant pairs. the number of discordant pairs.
And the final Kendall's correlation coefficient is the average of all trials from each appraiser:
-

where
-
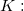 the number of trials for each appraiser vs standard, otherwise for all appraisers vs standard, the number of trials for each appraiser vs standard, otherwise for all appraisers vs standard, 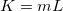 , where , where 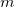 is the number of trials and is the number of trials and 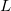 is the number of appraisers. is the number of appraisers.
Testing Significance of Kendall's Correlation Coefficient
When the standard is known, use the following formula for testing the significance of Kendall's correlation coefficient.
-

-

where
-
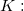 the number of trials for each appraiser vs standard, otherwise for all appraisers vs standard, the number of trials for each appraiser vs standard, otherwise for all appraisers vs standard, 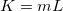 , where , where 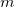 is the number of trials and is the number of trials and 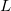 is the number of appraisers. is the number of appraisers.
-
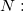 the total number of samples. the total number of samples.
-
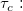 the calculated Kendall's correlation coefficient. the calculated Kendall's correlation coefficient.
|