確率プロットとQ-Qプロット
ProbPlot-QQPlot
データセットが与えられた分布に従うかどうか検定するために確率プロットを使用します。これは、X軸上に観測した累積パーセント、Y軸上に期待累積パーセントを持つグラフを表示します。すべてのデータポイントが参照線に近い場合、データセットは与えられた分布に従うものと結論付けできます。
Q-Q(Quantile-Quantile) プロットは、データセットが与えられた分布に従うかどうかを検定するもう一つの手法です。確率プロットとは異なり、XとY軸上でパーセントの代わりに観測値と期待値を示します。すべてのデータポイントが参照線に近い場合、データセットは与えられた分布に従うものと結論付けできます。
Originでは、4つの分布(正規, 正規対数, 指数, ワイブル, ガンマ)と5つのパーセンタイル近似のプロット手法(Blom, Benard,
Hazen, Van der Waerden, Kaplan-Meier)をサポートしています。
確率プロット/Q-Qプロットを作成するには
確率プロット、または、Q-Qプロットを作成するには、
- 1つのY列または複数のY列を入力変数として選択します。
- 確率/Q-Qプロットダイアログを開きます。
- 確率プロット:Originのメインメニューで、作図 > 統計:確率プロット(P-P図)を選択します。
または、2Dグラフギャラリーツールバーの確率プロットボタン
 をクリックします。 をクリックします。
- Q-Qプロット:Originのメインメニューで、作図 > 統計:Q-Qプロットを選択します。 または、2DグラフギャラリーツールバーのQ-Qプロットボタン
 をクリックします。 をクリックします。
- plot_prob Xファンクションダイアログで、グループ化列を選択し、グループと変数の配置を設定して分布と手法を指定します。
- OKをクリックして確率プロット、または、Q-Qプロットを作成します。

plot_probXファンクションのダイアログ
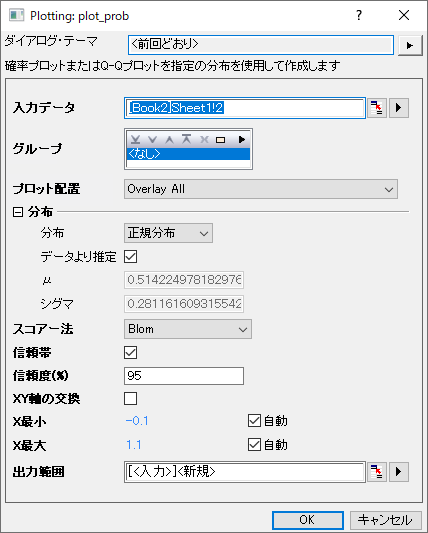
入力データ |
入力データを指定します。入力変数として複数の列を選択できます。 |
グループ |
入力変数を複数のプロットに分割するためのグループ化列を指定します。 |
プロット配置 |
プロットを各変数およびグループで配置する方法を指定します。
- すべて重ねる:デフォルトで選択されます。同じレイヤ内にすべてのグループと変数が配置されます。
- グループを重ねて変数は別レイヤ: 異なるグループが同じレイヤに重ねて表示され、変数毎に別のレイヤに描画されます。
- 変数を重ねてグループは別レイヤ: 異なる変数が同じレイヤに重ねて表示され、グループ毎に別のレイヤに描画されます。
|
分布 |
データの分布の種類を指定します。分布についてのより詳細な情報は、分布セクションを参照してください。
- 分布
- 以下の分布から選択します。
- データから推定
- 入力データから分布パラメータを推定するかどうかを指定します。チェックを付けない場合、パラメータを手動で指定することができます。
- u
- 正規分布の平均
- シグマ
- 正規分布の標準偏差
- 形状
- 指定した分布の形状。正規対数、Weibull、ガンマの分布で利用可能です。
- スケール
- 指定した分布のスケール。正規対数、指数分布、Weibull、ガンマの分布で利用可能です。
|
スコア法 |
パーセンタイル近似のプロット方法を選択します。手法についてのより詳細な情報は、スコア法セクションを参照してください。
- Blom
- Benard
- Hazen
- Van der Waerden
- Kaplan-Meier
|
信頼帯 |
確率プロとに信頼帯を出力するか指定します。計算の詳細はアルゴリズムを参照してください。
|
信頼水準(%) |
信頼帯が選択されている場合にのみ使用できます。選択した分布の信頼水準を%で指定します。 |
| X軸とY軸の交換 |
X軸とY軸の位置を交換するか指定します。 |
X最小
X最大 |
自動の値は、X最小 = 1 および X最大 = 99.5です。自動のチェックを外すと、出力の参照線列の最小および最大値を使用します。
X最大が自動の値より大きい場合、X最大のパーセント値p1を計算して、 パーセンタイル列には、デフォルトリストにp1およびp1より大きい値のみ含める必要があります。X最大が自動の値より小さい場合、X最大のパーセント値p2を計算して、
パーセンタイル列には、デフォルトリストにp2およびp2より小さい値のみ含める必要があります。
X最小が自動の値よりも小さい場合、X最小値のパーセンタイル値p1を計算します。p1<1e-5, p1=1e-5の場合、p1よりも大きい最小値10^(-m)を見つけ、パーセンタイル列には
p1, 10^(-m), 10^(-m+1), ,,,,1, 2,...が含まれます。
X最大が自動の値よりも大きい場合、X最大値のパーセンタイル値p2を計算します。p2>99.99, p2=99.99の場合、リスト
(99.9, 99.99) から2より小さい最大値をみつけ、パーセンタイル列には99, 99.5, 99.9,..p2.が含まれます。
|
出力範囲 |
これにより、グラフ用に計算されたデータの保存場所を決定します。 |
分布
Originには4つの確率分布とQ-Qプロットが含まれます。 次の表に、密度関数を示します。
| 分布 |
密度関数 p(x) |
範囲 |
パラメータ |
正規分布 |
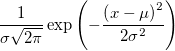
|
全ての  |
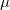 平均は、位置パラメータ 平均は、位置パラメータ
で、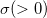 標準偏差は、スケールパラメータです。 標準偏差は、スケールパラメータです。
|
対数正規 |
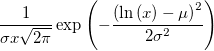
|
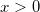
|
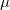 は形状パラメータ、 は形状パラメータ、
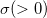 はスケールパラメータです。 はスケールパラメータです。
|
指数分布 |
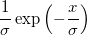
|
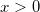
|
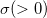 はscaleパラメータです。 はscaleパラメータです。 |
ワイブル |
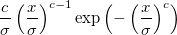
|
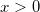
|
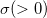 はスケールパラメータ、 はスケールパラメータ、
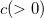 は形状パラメータです。
は形状パラメータです。
|
ガンマ |
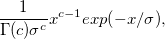
|
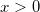
|
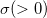 はスケールパラメータ、 はスケールパラメータ、
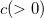 は形状パラメータです。
は形状パラメータです。
|
確率プロット作成の詳細
確率プロットを作成するために、観測されたデータセットを最小から最大にソートします。
![x[1]\le x[2]\le x[3]\le \cdots \le x[n-1]\le x[n] x[1]\le x[2]\le x[3]\le \cdots \le x[n-1]\le x[n]](//d2mvzyuse3lwjc.cloudfront.net/doc/ja/UserGuide/images/Probability_Plot_and_Q-Q_Plot/math-5624a30d4c678dc72eae5846b1e79702.png) , , 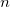 は観測されたデータセットの総数です。 は観測されたデータセットの総数です。
ソートされた観測値は、X座標は![x[i]\ x[i]\](//d2mvzyuse3lwjc.cloudfront.net/doc/ja/UserGuide/images/Probability_Plot_and_Q-Q_Plot/math-92f8cb93ad9350ca1ab67868f3667559.png) で、Y座標はスコア法用いて計算された点によってプロット上で示されます。 で、Y座標はスコア法用いて計算された点によってプロット上で示されます。
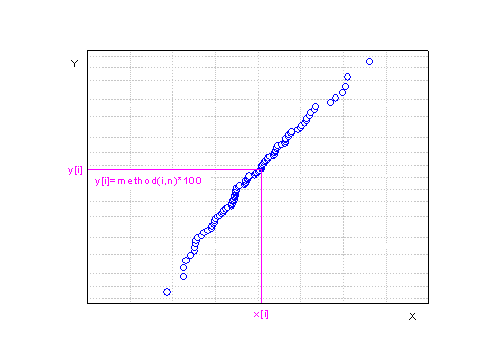
確率プロットのスケールタイプは、分布により異なります。
| 分布 |
Xスケールタイプ |
Yスケールタイプ |
正規分布 |
線形 |
確率 |
対数正規 |
Ln |
確率 |
指数分布 |
Ln |
二重対数逆数 |
ワイブル |
Log10 |
二重対数逆数 |
ガンマ |
Log10 |
確率 |
Q-Qプロット作成の詳細
Q-Qプロットを作成するために、観測されたデータセットを最小から最大にソートします。
![x[1]\le x[2]\le x[3]\le \cdots \le x[n-1]\le x[n] x[1]\le x[2]\le x[3]\le \cdots \le x[n-1]\le x[n]](//d2mvzyuse3lwjc.cloudfront.net/doc/ja/UserGuide/images/Probability_Plot_and_Q-Q_Plot/math-5624a30d4c678dc72eae5846b1e79702.png) ( (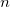 は観測値の総数) は観測値の総数)
Y値は、使用されるスコア法の逆累積分布関数です。
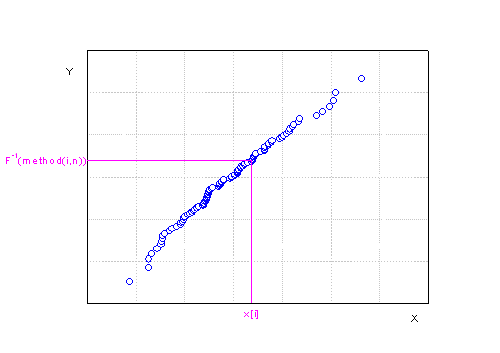
スコア法
入力データが最小から最大の順に並べられ、ソートされたデータのシリアル番号が以下のいずれかの方法で採点されます。 この表では、 はシリアル番号で、 はシリアル番号で、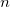 は欠損なしの入力データの総数です。 は欠損なしの入力データの総数です。
| メソッド |
プロット位置 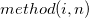 |
Blom |
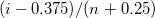
|
Benard |
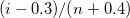
|
Hazen |
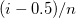
|
Van der Waerden |
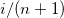
|
Kaplan-Meier |
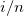
|
参考文献
- Samuel Kotz , Campbell B. Read , N. Balakrishnan, Brani Vidakovic,
2005.Encyclopedia of statistical sciences., NewYork: John Wiley
& Sons, Inc.
- Thode, Henry C. 2002, Testing for Normality, CRC Press
|