パラメータ初期化
FitPara-INI
Levenberg-Marquardt反復アルゴリズムは、フィット処理を開始するのに、初期値を必要とします。適切な初期値を与えると、素早く、信頼できる収束結果を得ることができます。関数オーガナイザでフィット関数を定義するとき、『パラメータ設定』ボックスで初期値を割り当てることができ、『パラメータ初期化』ボックスに初期値を計算するのに使用するOrigin Cコードを入力します。
OriginのNLFitは、すべての組み込み関数に対して、自動初期値計算ルーチンを提供しています。ユーザ定義関数では、パラメータ初期化コードを自分で追加する必要があります。パラメータ初期化コードが無い場合、NLFitが開始するとき、すべてのパラメータ値が欠損値になります。この場合、フィット処理を開始するときに、推定される初期値を入力する必要があります。
仮に「パラメータ設定」で異なる初期値が設定されていたとしても、パラメータ初期化ルーチンにより推定されるパラメータの初期値が使われます。
「パラメータ設定」ダイアログで初期値を設定する
パラメータ設定ボックスの近くにある ボタンをクリックし、パラメータ設定ダイアログを開きます。そして、パラメータタブの「値」列にパラメータの適切な初期値を入力できます。 ボタンをクリックし、パラメータ設定ダイアログを開きます。そして、パラメータタブの「値」列にパラメータの適切な初期値を入力できます。
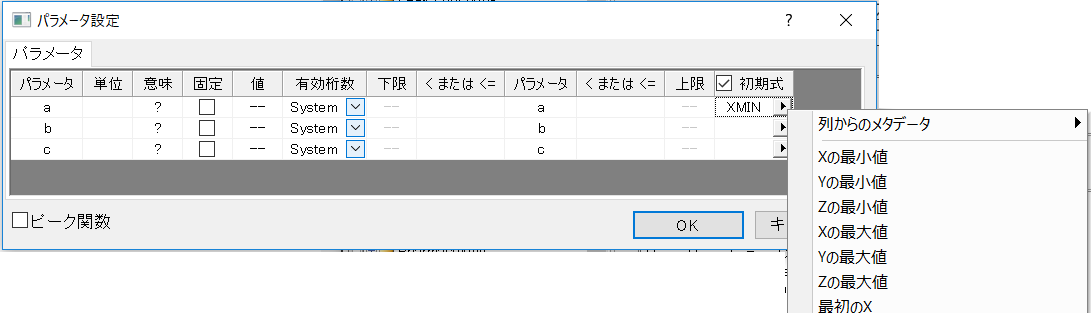
初期式(列統計値、ラベル行など)でパラメータを初期化するには、初期式のチェックボックスのチェックを入れて、初期式やメタデータをフライアウトメニューから選択します。
Origin Cコードでパラメータの初期値を推定する
『パラメータ初期化』のテキストボックスには、パラメータの初期化コードが含まれます。組込み関数に対して、これらのルーチンは データセット特有のパラメータを推定することでフィット前にパラメータ値を効果的に推定することができます。新しいOrigin Cフィット関数を定義するとき、 ボタンをクリックして、コードビルダで初期化コードを編集することができます。 ボタンをクリックして、コードビルダで初期化コードを編集することができます。
パラメータの初期値を推定する方法は、多くありますが、一般に関数を変換して、元データに基づく値を推定します。例えば、MyFuncという名前のフィットモデルを次のように定義できます。
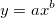
(これは、Originの組込のAllometric1関数と同じ関数です。)
そして、数式は次のような式で変換されます。
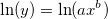 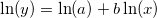
変換すると、ln(y) と ln(x)の間に線形の関係を持ち、切片と勾配がそれぞれ、ln(a)とb になります。推定パラメータ値を取得するには、単純な線形フィットを行う必要があります。初期化コードは次のようになります。
#include <origin.h> void _nlsfParamMyFunc( // フィットパラメータ: double& a, double& b, // 独立データセット: vector& x_data, // 独立データセット: vector& y_data, // 曲線: Curve x_y_curve, // 補助的なエラーコード: int& nErr) { // 編集可能部分の開始 sort( x_y_curve ); // 曲線のソート Dataset dx; x_y_curve.AttachX(dx); // Xデータにデータセットオブジェクトを付加 dx = ln(dx); // x = ln(x)を設定 x_y_curve = ln( x_y_curve ); //y = ln(y)を設定 vector coeff(2); fitpoly(x_data, y_data, 1, coeff); // 一次 (単一線形)多項式フィット a = exp( coeff[0] ); // パラメータaの推定 b = coeff[1]; // パラメータbの推定 // 編集可能部分の終了 }
コードビルダで、関数本体を編集する必要があります。パラメータ、独立変数、従属変数が関数定義で宣言されます。さらに、Originのオブジェクトのいくつかは宣言されています。各独立変数と従属変数のDatasetオブジェクトおよび各xyデータのCurveオブジェクトが宣言されています。
vector& x_data; vector& y_data; Curve x_y_curve;
Vectorはxとyのキャッシュ入力値を表し、これらは変更されません。curveオブジェクトは、xデータセットとyデータセットで構成されるデータセットの曲線の複製で、一番いいフィットを探しているデータです。
これらの宣言の下に、編集可能なセクション(白い領域)があり、初期化コードを入力することができます。関数の定義はC言語のシンタックスに従う必要があります。
| Note:void型の関数は、関数が値を戻さないということです。パラメータの変数は、関数コードに保存されます。 |
初期化は、vectorまたはcurveオブジェクトを引数として、組込み関数を呼び出すことで行われます。初期化関数を定義したら、シンタックスが正しいかどうかを確認します。これを行うには、コードビルダの上の方にある「コンパイル」ボタンをクリックします。これは、Origin Cコンパイラを使って、関数コードをコンパイルします。コンパイル中に発生したエラーは、ワークスペースの下にあるコードビルダの出力ウィンドウに出力されます。
初期化コードを定義して、コンパイルしたら、ウィンドウの上部にあるNLSFに戻るボタンをクリックし、関数オーガナイザに戻ることができます。
コードをデバッグしたい場合、NLFitダイアログのコードタブからコードビルダの初期化コードを開き、切断点を設定します。そして、パラメータ初期化ボタン をクリックして初期化コードを呼び出し、デバッグします。デバッグに関する詳細は、Originメニューからヘルプ:プログラミング:コードビルダを選択し、デバッグを検索して下さい。 をクリックして初期化コードを呼び出し、デバッグします。デバッグに関する詳細は、Originメニューからヘルプ:プログラミング:コードビルダを選択し、デバッグを検索して下さい。 |
パラメータ初期化によく使われるOrigin Cファンクション
パラメータ初期化の例
指数関数
サンプル関数
- EXPDEC2
方程式
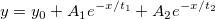
初期化コード
int sign; t1 = get_exponent(x_data, y_data, &y0, &A1, &sign); t1 = t2 = -1 / t1; A1 = A2 = sign * exp(A1) / 2;
説明
ほとんどの指数曲線が類似しているため、複雑な方程式へのアプローチには単純な指数関数を使うことができます。このEXPDEC2関数は、パラメータがget_exponentからくる2つの基本的な指数関数の組み合わせとして扱うことができます。
ピーク関数
サンプル関数
- LORENTZ
方程式
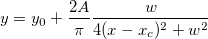
初期化コード
xc = peak_pos(x_y_curve, &w, &y0, NULL, &A); A *= 1.57*w;
説明
この初期化コードでは、まず初めにピーク幅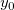 、基線 、基線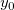 、ピークの中心 、ピークの中心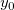 、元はpeak_pos関数によって変数 、元はpeak_pos関数によって変数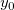 とされていたピークの高さを測定します。以下の演算でピーク面積Aを求めます。 とされていたピークの高さを測定します。以下の演算でピーク面積Aを求めます。
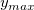 は は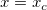 の値とします。 の値とします。
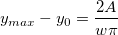
and
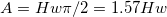
ここで、H はピークの高さです。
シグモイド関数
サンプル関数
- DRESP
方程式
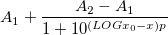
初期化コード
sort(x_y_curve); A1 = min( y_data ); A2 = max( y_data ); LOGx0 = xaty50( x_y_curve ); double xmin, xmax; x_data.GetMinMax(xmin, xmax); double range = xmax - xmin; if ( yatxmax(x_y_curve) - yatxmin(x_y_curve) > 0) p = 5.0 / range; else p = -5.0 / range;
説明パラメータの意味を知ることは、パラメータの初期化に非常に役立つ重要なことです。用量反応において、A1は下の漸近線 、A2は上の漸近線を意味するので、Yの最小値と最大値で初期化を行うことができます。反応におけるパラメータLOGx0 は、50%の反応がおこる典型的な値なので、ここではxaty50関数を使います。傾きpに関しては、この値をどのように計算しても問題ありませんが、傾きの符号は重要です。
曲面関数
サンプル関数
- Gauss2D
方程式
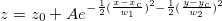
初期化コード
Curve x_curve, y_curve; bool bRes = get_interpolated_xz_yz_curves_from_3D_data(x_curve, y_curve, x_data, y_data, z_data, true); if(!bRes) return; xc = peak_pos(x_curve, &w1, &z0, NULL, &A); yc = peak_pos(y_curve, &w2);
説明
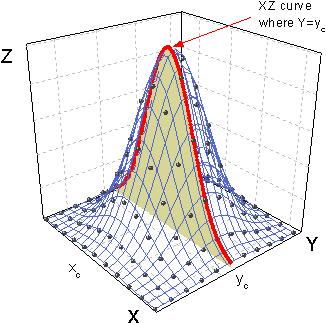
曲線関数の初期値を測定する一つの方法は、平面で問題を解くことです。このGauss2D関数を例にとると、Zの最大値は点(xc, yc)上にあるのが明らかなので、 get_interpolated_xz_yz_curves_from_3D_data 関数を使ってXZとYZ平面での特徴的な曲線を求めることができます。そして、peak_pos 関数を使ってピーク幅、高さなどの他のピークの属性を測定します。
|