Parameterinitialisierung
FitPara-INI
Der iterative Algorithmus Levenberg-Marquardt benötigt Initialisierungswerte zum Starten des Anpassungsvorgangs. Gute Ergebnisse der Parameterinitialisierung mit schnellem und zuverlässigen Modell/Datenkonvergenz. Beim Definieren einer Anpassungsfunktion im Funktionsorganizer können Sie die Initialisierungswerte im Feld Parametereinstellungen festlegen oder Origin C-Code im Feld Parameterinitialisierung eingeben, mit dem die Startwerte abgeschätzt werden können.
NLFit stellt einen automatischen Parameterinitialisierungscode für alle Standardfunktionen zur Verfügung. Bei benutzerdefinierten Funktionen sollten Sie Ihren eigenen Code zur Initialisierung der Parameter eingeben. Ist kein Parameterinitialisierungscode gegeben, werden alle Parameterwerte zu fehlenden Werten, wenn NLFit startet. In diesem Fall müssen Sie grob geschätzte Parameterwerte zum Starten des iterativen Anpassungsprozesses eingeben.
Beachten Sie, dass durch Parameterinitialisierungsroutinen geschätzte Startwerte für Parameter verwendet werden, auch wenn andere Werte im Dialog Parametereinstellungen definiert wurden.
Initialisierungswerte im Dialog Parametereinstellungen festlegen
Klicken Sie auf die Schaltfläche  neben dem Feld Parametereinstellungen, um den Dialog Parametereinstellungen zu öffnen. Sie können dann die geeigneten Initialisierungswerte für die Parameter in der Spalte Wert der Registerkarte Parameter eingeben: neben dem Feld Parametereinstellungen, um den Dialog Parametereinstellungen zu öffnen. Sie können dann die geeigneten Initialisierungswerte für die Parameter in der Spalte Wert der Registerkarte Parameter eingeben:
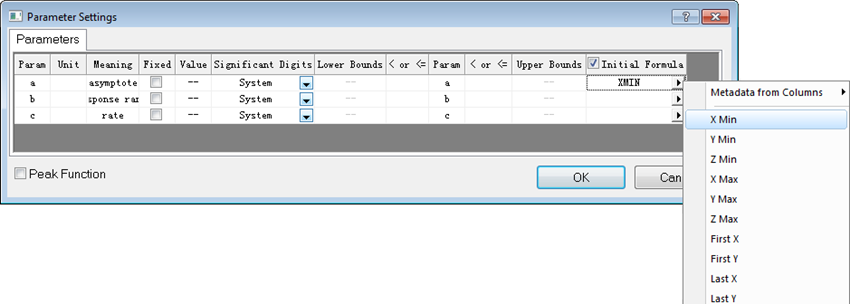
Um Parameter mit der Initialisierungsformel zu initialisieren (Werte der Spaltenstatistik, Beschriftungszeilen etc.), können Sie das Kontrollkästchen der Spalte Initialisierungsformel aktivieren und die gewünschte Initialisierungsformel bzw. Metadaten im Ausklappmenü auswählen.
Parameterinitialisierungswerte durch Origin C-Code schätzen
Das Textfeld bei Parameterinitialisierung beinhaltet den Parameterinitialisierungscode. Bei Standardfunktionen können diese Routinen vor dem Anpassen tatsächlich Parameterwerte schätzen, indem datensatzspezifische Parameterschätzungen ausgeführt werden. Wenn Sie eine neue Origin C-Anpassungsfunktion definieren, können Sie den Initialisierungscode mit Hilfe des Code Builders bearbeiten, indem Sie auf die Schaltfläche  klicken. klicken.
Auch wenn es sehr viele Methoden zum Schätzen der Parameterstartwerte gibt, werden wir im Allgemeinen die Funktion umformen und, basierend auf den Rohdaten, den Wert ableiten. Wir können zum Beispiel ein Anpassungsmodell namens MyFunc wie folgt definieren:
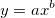
(Dies ist die gleiche Funktion, wie die standardmäßige Allometric1-Funktion in Origin)
Anschließend wird die Gleichung umgeformt:
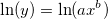 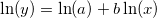
Nach der Umformung haben wir eine lineare Beziehung zwischen ln(y) und ln(x), und der Schnittpunkt ist ln(a) und die Steigung b. Anschließend müssen wir nur noch eine einfache lineare Anpassung ausführen, um die geschätzten Parameterwerte zu erhalten. Der Initialisierungscode kann wie folgt aussehen:
#include <origin.h> void _nlsfParamMyFunc( // Fit Parameter(s): double& a, double& b, // Independent Dataset(s): vector& x_data, // Dependent Dataset(s): vector& y_data, // Curve(s): Curve x_y_curve, // Auxilary error code: int& nErr) { // Beginning of editable part sort( x_y_curve ); // Sort the curve Dataset dx; x_y_curve.AttachX(dx); // Attach an Dataset object to the X data dx = ln(dx); // Set x = ln(x) x_y_curve = ln( x_y_curve ); // Set y = ln(y) vector coeff(2); fitpoly(x_data, y_data, 1, coeff); // One order (simple linear) polynomial fit a = exp( coeff[0] ); // Estimate parameter a b = coeff[1]; // Estimate parameter b // End of editable part }
Im Code-Builder müssen Sie nur die eigentliche Funktion bearbeiten. Die Parameter, die unabhängigen und die abhängigen Variablen werden in der Funktionsdefinition deklariert. Zusätzlich werden einige Origin-Objekte definiert: Für jede der unabhängigen und abhängigen Variablen wird ein Datensatzobjekt und für jedes XY-Datenpaar ein Kurvenobjekt definiert:
vector& x_data; vector& y_data; Curve x_y_curve;
Die Vektoren stellen die Eingabe von X- und Y-Werten im Zwischenspeicher dar, die niemals geändert werden sollten. Und das Kurvenobjekt ist eine Kopie der Datensatzkurve, die aus einem X-Datensatz und einem Y-Datensatz besteht, für die Sie versuchen, die beste Anpassung zu finden.
Unter diesen Deklarationsanweisungen befindet sich ein editierbarer Abschnitt – die weiße Fläche - die für den Initialisierungscode reserviert ist. Bitte beachten Sie, dass die Syntax der Funktionsdefinition mit der Syntax der Programmiersprache C übereinstimmt.
| Beachten Sie zudem, dass die Funktion vom Typ void ist, was bedeutet, dass sie keinerlei Werte zurückgibt. Stattdessen werden die Parametervariablen im Funktionscode gespeichert. |
Die Initialisierung der Parameter wird also dadurch erreicht, dass Standardfunktionen, die Datensätze oder Kurven als Argumente erwarten, entsprechende Werte berechnen. Sobald Sie die Funktion zur Initialisierung der Parameter geschrieben haben, sollten Sie sicherstellen, dass die Syntax korrekt ist. Klicken Sie dazu auf die Schaltfläche Kompilieren im oberen Teil des Arbeitsbereichs. Dadurch wird der Funktionscode mit dem Origin C Compiler kompiliert. Eventuell auftretende Fehler im Kompilierungsprozess werden im Ausgabefenster des Code-Builders im unteren Teil des Arbeitsbereichs angezeigt.
Sobald der Initialisierungscode definiert und kompiliert worden ist, können Sie mit einem Klick auf die Schaltfläche Zurück zum Dialog im oberen Teil des Arbeitsbereichs zum Funktionsmanager zurückkehren.
Hinweis: Wenn Sie Ihren Code debuggen möchten, können Sie den Initialisierungscode im Code Builder über den Dialog NLFit auf der Registerkarte Code öffnen und Haltepunkte festlegen. Klicken Sie dann auf die Schaltfläche Parameter initialisieren  , um den Initialisierungscode aufzurufen und zu debuggen. Weitere Informationen zum Debuggen erhalten Sie, wenn Sie Hilfe: Programmierung: Code Builder… im Origin-Menü auswählen und nach "debug" suchen. , um den Initialisierungscode aufzurufen und zu debuggen. Weitere Informationen zum Debuggen erhalten Sie, wenn Sie Hilfe: Programmierung: Code Builder… im Origin-Menü auswählen und nach "debug" suchen. |
Häufig verwendete Origin C-Funktion zur Parameterinitialisierung
| Function |
Beschreibung |
|
Fläche
|
Berechnen der Fläche unter einer Kurve
|
|
Curve_MinMax
|
Berechnen des X- und Y-Bereichs der Kurve
|
|
Curve_x
|
Berechnen des X-Werts einer Kurve bei festgelegtem Index
|
|
Curve_xfromY
|
Berechnen des interpolierten/extrapolierten X-Werts einer Kurve bei festgelegtem Y-Wert
|
|
Curve_y
|
Berechnen des Y-Werts einer Kurve bei festgelegtem Index
|
|
Curve_yfromX
|
Gibt den interpolierten/extrapolierten Wert von Y bei festgelegtem Wert von X für eine gegebene Kurve zurück.
|
|
fitpoly
|
Passt eine polynomiale Gleichung an eine Kurve (oder einen XY-Vektor) an und gibt die Koeffizienten und statistischen Ergebnisse zurück.
|
|
fit_polyline
|
Passt die Kurve an eine Polylinie an, wobei n die Anzahl der Abschnitte ist, und berechnet den Durchschnittswert der X-Koordinaten jedes Abschnitts.
|
|
fitpoly_range
|
Passt eine polynomiale Gleichung an den Bereich einer Kurve an.
|
|
find_roots
|
Sucht Punkte mit festgelegter Höhe.
|
|
FWHM
|
Berechnet die Peakbreite einer Kurve bei dem halben Maximalwert von Y.
|
|
get_exponent
|
Diese Funktionen werden verwendet, um y0, R0 und A in y = y0 + A*exp(R0*x) zu schätzen.
|
|
get_interpolated_xz_yz_curves_from_3D_data
|
Interpoliert 3D-Daten und gibt geglättete XZ, YZ-Kurven zurück.
|
|
ocmath_xatasymt
|
Berechnet den Wert von X bei einer vertikalen Asymptote.
|
|
ocmath_yatasymt
|
Berechnet den Wert von X bei einer horizontalen Asymptote.
|
|
peak_pos
|
Diese Funktion wird verwendet, um XY-Koordinaten, Breite und Fläche etc. des Peaks zu schätzen.
|
|
sort
|
Verwendet ein Kurvenobjekt, um einen Y-Datensatz entsprechend einem X-Datensatz zu sortieren.
|
|
Vectorbase::GetMinMax
|
Berechnet minimale und maximale Werte und ihre Indizes von einem Vektor aus.
|
|
xatasymt
|
Berechnet den Wert von X bei einer vertikalen Asymptote.
|
|
xaty50
|
Berechnet den interpolierten Wert von X beim Mittel von Minimum und Maximum der Y-Werte einer Kurve.
|
|
xatymax
|
Berechnet den Wert von X beim maximalen Wert von Y einer Kurve.
|
|
xatymin
|
Berechnet den Wert von X beim minimalen Wert von Y einer Kurve.
|
|
yatasymt
|
Berechnet den Wert von X bei einer horizontalen Asymptote.
|
|
yatxmax
|
Berechnet den Wert von Y beim maximalen X-Wert einer Kurve.
|
|
yatxmin
|
Berechnet den Wert von Y beim minimalen X-Wert einer Kurve.
|
Weitere Beispiele für die Parameterinitialisierung
Exponentenfunktion
Beispielfunktion
- ExpDec2
Gleichung
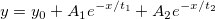
Initialisierungscode
int sign; t1 = get_exponent(x_data, y_data, &y0, &A1, &sign); t1 = t2 = -1 / t1; A1 = A2 = sign * exp(A1) / 2;
Beschreibung
Da die meisten der exponentiellen Kurven sich ähneln, können wir eine einfache Exponentialfunktion für eine Annäherung an komplexe Gleichungen verwenden. Diese EXPDEC2-Funktion kann als Kombination zweier grundlegender Exponentialfunktionen behandelt werden, deren Parameter aus get_exponent stammen.
Peakfunktion
Beispielfunktion
- Lorentz
Gleichung
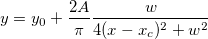
Initialisierungscode
xc = peak_pos(x_y_curve, &w, &y0, NULL, &A); A *= 1.57*w;
Beschreibung
In diesem Initialisierungscode werten wir zunächst die Peakbreite 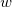 , den Wert der Basislinie , den Wert der Basislinie 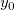 , das Peakzentrum , das Peakzentrum 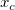 und die Peakhöhe aus, die ursprünglich der Variable und die Peakhöhe aus, die ursprünglich der Variable 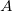 durch die Funktion peak_pos zugewiesen sind. Der Peakbereich A wird dann mit Hilfe der folgenden Ableitung berechnet: durch die Funktion peak_pos zugewiesen sind. Der Peakbereich A wird dann mit Hilfe der folgenden Ableitung berechnet:
Angenommen 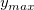 ist der Wert, bei dem ist der Wert, bei dem 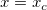 , dann haben wir: , dann haben wir:
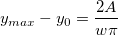
und
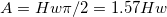
Wobei H die Peakhöhe ist.
Sigmoidale Funktion
Beispielfunktion
- DRESP
Gleichung
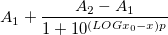
Initialisierungscode
sort(x_y_curve); A1 = min( y_data ); A2 = max( y_data ); LOGx0 = xaty50( x_y_curve ); double xmin, xmax; x_data.GetMinMax(xmin, xmax); double range = xmax - xmin; if ( yatxmax(x_y_curve) - yatxmin(x_y_curve) > 0) p = 5.0 / range; else p = -5.0 / range;
Beschreibung
Das Wissen über die Parameterbedeutungen ist sehr hilfreich und wichtig für die die Parameterinitialisierung. In der Dose-Response-Reaktion sind A1 und A2 die untere bzw. obere Asymptote, so dass wir sie mit dem minimalen und maximalen Y-Werten initialisieren können. Der Parameter LOGx0 in der Reaktion ist ein typischer Wert für eine 50%-Reaktion. Deshalb verwenden wir hier die Funktion xaty50. Die Berechnungsmethode des Steigungswerts p bleibt Ihnen überlassen, allerdings ist das Vorzeichen der Steigung wichtig.
Oberflächenfunktion
Beispielfunktion
- Gauss2D
Gleichung
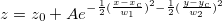
Initialisierungscode
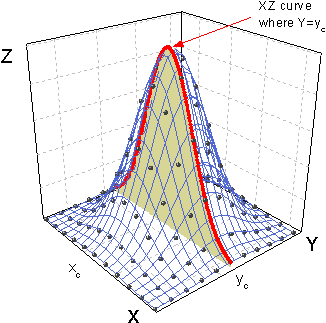
Curve x_curve, y_curve; bool bRes = get_interpolated_xz_yz_curves_from_3D_data(x_curve, y_curve, x_data, y_data, z_data, true); if(!bRes) return; xc = peak_pos(x_curve, &w1, &z0, NULL, &A); yc = peak_pos(y_curve, &w2);
Beschreibung
Eine Idee zum Auswerten der Inistialisierungswerte von Oberflächenfunktionen ist das Lösen des Problems in einer Ebene. Bei der Funktion Gauss2D beispielsweise ist es recht offensichtlich, dass der maximale Z-Wert sich im Punkt (xc, yc) befindet, so dass wir die Funktion get_interpolated_xz_yz_curves_from_3D_data verwenden können, um die charakteristische Kurve in der XZ- und YZ-Ebene zu erhalten. Dann wird die Funktion peak_pos verwendet, um andere Peakattribute wie Breite, Höhe etc. auszuwerten.
|