等高線図を作成するCreate-Contour-Graph
等高線図は2Dで表されるサーフェスグラフです。 等高線図の表示は、XZ平面に垂直な視点から3D曲面図を表示するのと同じです。 等高線図では、Z値の範囲は、異なる色またはグレースケールのレベル、等高線ラベルで区別されます。
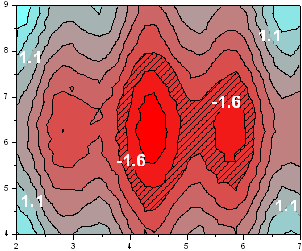
等高線グラフの種類
Originは7種類の等高線図を提供しています。
| グラフの種類
|
ワークシート上のXYZ形式
|
行列ウィンドウ
|
ワークシート上の仮想行列
|
- 等高線 - カラーマップ
- 等高線 - 線+ラベル
- グレースケール等高線図
- ヒートマップ
|
可 (ヒートマップ以外)
|
可
|
可
|
|
|
可
|
可
|
不可
|
|
|
可
|
不可
|
不可
|
『(作図の詳細) カラーマップ/等高線』、『ラベル』タブを使って、等高線図を編集します。
Originの等高線図は、行列データ、ワークシートデータ、仮想行列データから作成できます。ワークシートから直接等高線図を作成するよりも、行列から等高線図を作成するほうが高速なので、大きなデータを扱うには行列の手法の方がおすすめです。一方、XYZワークシートから等高線グラフを作成する場合、三角分割法を使って等高線を生成するので、行列を生成する必要はありません。
| Note: 生のXYでプロットする等高線の三角法アルゴリズムはOrigin 2016で実行されました。以前のバージョンでは、X,Yデータに対する正規化が作図の前にいくつか行われていました。バージョン2016以降、XYZワークシートデータでの等高線図及び3D曲面は、 以前のバージョンで作成された同じデータとは、異なっています。この変更は、X値とY値の間でスケール範囲が大きく異なる場合に顕著に現れてきます。詳細は FAQ-822をご覧ください。
|
他に、XYZワークシートから等高線を作成することには次のようなメリットがあります。
- レイヤ境界、データ境界、カスタム境界, をサポート
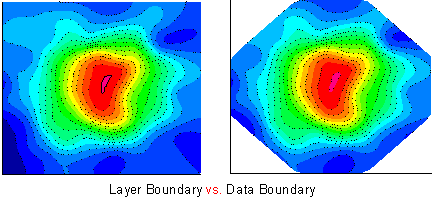
- 三点等高線図をサポート
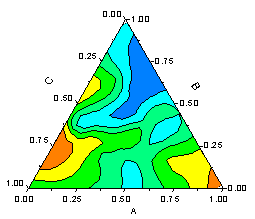
XYZデータあるいは仮想行列から作成された等高線図は非線形のX/Y軸をサポートしています。行列ウィンドウから作成された等高線図は線形軸のみサポートします。
 | Origin 2018より前は、カスタム境界を適用すると境界マージンに不完全な色塗りが生成されることがありました。これはバージョン2018で改善されました。システム変数 @TCSM を使って、以前の不具合現象を修正することが可能です。

|
等高線グラフの作成および編集方法
行列データから等高線図を作成するには、対応するボタンをクリックするか、作図メニューから対応する項目を選択します。 XYZデータから等高線図を作成するには、Z列を作成するかどの列も選択しない状態で上記2つの方法のうち、片方を実行します。仮想行列で等高線図を作成するには、ワークシート内の全ての元データを選択してから上記方法の片方を実行します。すると、Originは内部的仮想行列とグラフを作成するダイアログを開きます。 仮想行列からグラフを作成することについての詳細は、仮想行列から3Dおよび等高線図を作成するをご覧ください。 各等高線図の種類については、等高線図で詳細を参照してください。
等高線図の編集に関しては軸ダイアログと作図の詳細ダイアログで行われます。軸ダイアログの詳細については、グラフ軸をご確認ください。作図の詳細ダイアログについての詳細は、 グラフを編集するをご覧ください。
等高線グラフの主な機能
等高線図には特殊な機能がいくつかあります。
等高線プロットからデータポイントを抽出
XYZ等高線図
XYZデータから等高線図を作成すると、等高線上で右クリックしてデータポイントを抽出を選択すると、データポイントを抽出: xyzgridダイアログを利用できます。X・Y方向のグリッドサイズと範囲を指定したり、列からXとYを指定したり、等高線内のポイントを取得したりして、指定したポイントでの補間データを、XYZまたは行列形式で新しいブックに出力できます。
アルゴリズムにあるように、指定されたグリッド点は三角分割法で計算され線形補間されます。
入力データ範囲の外側にある等高線の値は欠損値に設定されることに留意してください。
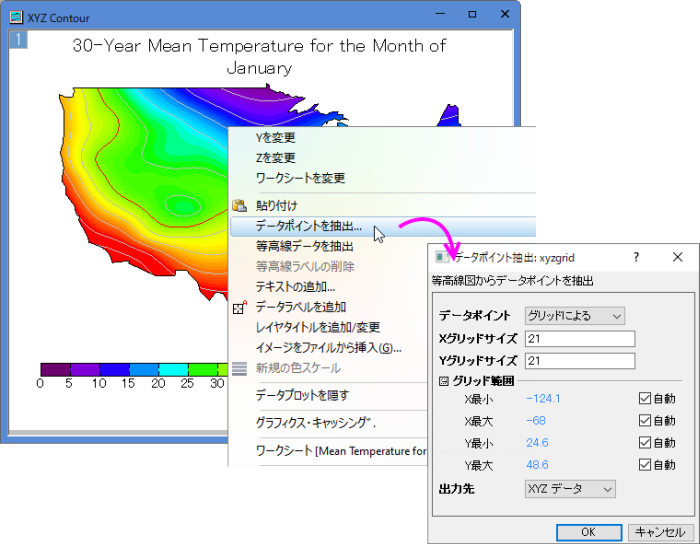
データポイントを抽出: xyzgridダイアログのダイアログコントロール
| データポイント
|
データポイントを抽出する手法を指定します。
|
| Xグリッドサイズ
|
グリッドによるデータポイントの抽出を選択する場合は、X方向に沿ったグリッド点の数を指定します。
|
| Yグリッドサイズ
|
グリッドによるデータポイントの抽出を選択する場合は、Y方向に沿ったグリッド点の数を指定します。
|
| グリッド範囲
|
グリッドによるデータポイントの抽出を選択する場合は、入力データ範囲の境界を指定します。デフォルトでは、すべてのデータポイントが含まれます。不良データポイントどを除外するために、最小と最大のXY座標を編集することで入力データの制限が可能です(Note: 入力データ範囲外の等高線値は欠損値として扱われます。)
- X最小
- 出力XYZ/行列データの最小のX値
- X最大
- 出力XYZ/行列データの最大のX値
- Y最小
- 出力XYZ/行列データの最小のY値
- Y最大
- 出力XYZ/行列データの最大のY値
|
| 出力先
|
出力データの形式を指定します。
- XYZデータ
- 補間された等高線値をXYZデータ形式で出力します。
- 行列
- 補間された等高線値を行列形式で出力します。
|
| 入力
|
列によるデータポイントの抽出を選択する場合は、 対応するZ値を抽出するXY列の範囲を指定します。
|
| 出力先
|
出力データを指定します。
|
| ピック操作
|
グラフから選択でデータポイントを抽出する場合は、この選択ボタンをクリックし、グラフをダブルクリックして抽出するポイントを選択する。次に完了ボタンをクリックすると、新しいシート内にそのポイントのXYZが抽出されます。
|
仮想行列・行列等高線図
仮想行列・行列から等高線図を作成すると、等高線上で右クリックしてデータポイントを抽出を選択すると、データポイントを抽出: mgridダイアログを利用できます。そして、X・Y方向のグリッドサイズと範囲を指定したり、列からXとYを指定したり、等高線内のポイントを取得したりできます。欠損値の処理方法を指定し、指定されたグリッドポイントで補間された行列形式のデータを新しいブックに出力できます。
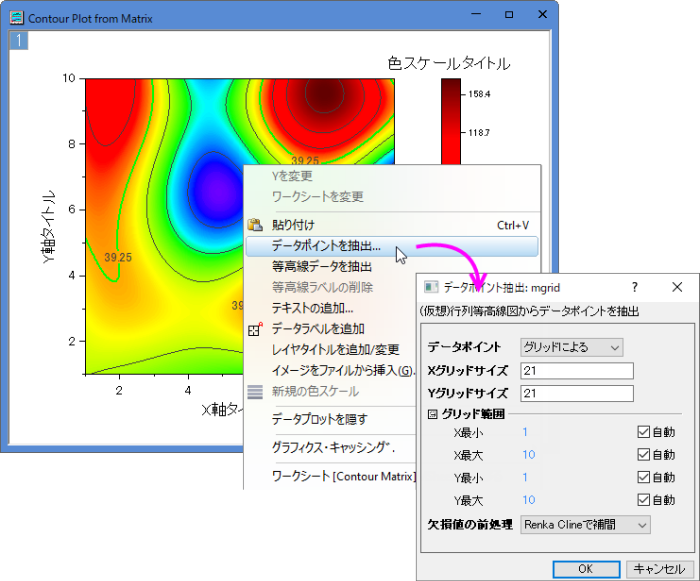
データポイントを抽出: mgridダイアログのダイアログコントロール
| データポイント
|
データポイントを抽出する手法を指定します。
|
| Xグリッドサイズ
|
グリッドによるデータポイントの抽出を選択する場合は、X方向に沿ったグリッド点の数を指定します。
|
| Yグリッドサイズ
|
グリッドによるデータポイントの抽出を選択する場合は、Y方向に沿ったグリッド点の数を指定します。
|
| グリッド範囲
|
グリッドによるデータポイントの抽出を選択する場合は、入力データ範囲の境界を指定します。デフォルトでは、すべてのデータポイントが含まれます。不良データポイントどを除外するために、最小と最大のXY座標を編集することで入力データの制限が可能です(Note: 入力データ範囲外の等高線値は欠損値として扱われます。)
- X最小
- 出力行列データの最小のX値
- X最大
- 出力行列データの最大のX値
- Y最小
- 出力行列データの最小のY値
- Y最大
- 出力行列データの最大のY値
|
| 欠損値の前処理
|
補間を使用してグリッドデータを生成するときに、欠損値を前処理する方法を指定します。
- スキップ
- 最初にすべての欠損値を削除してから補間を実行します。
- Renka Clineで補間
- Renka Cline: 任意の点Pに対して、Pを含む三角形の3つの頂点それぞれにおけるデータ値と勾配推定値を用いて補間値を計算します。
|
| 入力
|
列によるデータポイントの抽出を選択する場合は、 対応するZ値を抽出するXY列の範囲を指定します。
|
| 出力先
|
出力データを指定します。
|
| ピック操作
|
グラフから選択でデータポイントを抽出する場合は、この選択ボタンをクリックし、グラフをダブルクリックして抽出するポイントを選択する。次に完了ボタンをクリックすると、新しいシート内にそのポイントのXYZが抽出されます。
|
等高線ラベルの追加と削除
- 1つまたは2つの等高線のみに追加する場合は、次のように行います。
- Ctrl + Shiftキーを押しながら、ラベルを付ける等高線を正確にクリックします。選択した等高線を右クリックして、 等高線ラベルの付加 を選択します。
- 等高線を2回クリック (ダブルクリックではない) し、単一のレベル編集用のミニツールバーが表示されします。
- ドラッグしてラベルの位置を調整します。
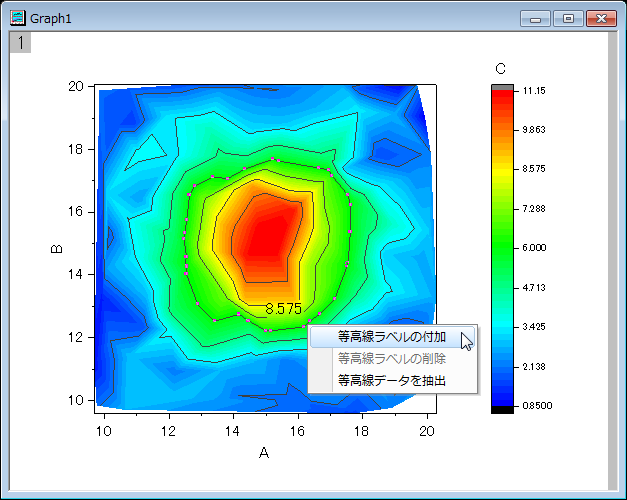
等高線ラベルの削除(非表示):
- カラーマップ/等高線タブを使います。ミニツールバーの等高線ラベルを表示ボタン
 をクリックして、等高線ラベルの表示を切り替えることもできます。 をクリックして、等高線ラベルの表示を切り替えることもできます。
- または、等高線レベルからすべてのラベルを削除するには、Ctrlキーを押しながらレベルを正確にクリックし、右クリックして等高線ラベルの削除を選択します。1つの等高線から(等高線レベル内で)ラベルを削除するには、CTRL + SHIFTを押して等高線を選択し、右クリックして等高線ラベルの削除を選択します。
等高線データの抽出
等高線データの抽出 では、Z値とXY座標、等高線に囲まれた面積を新規のワークシートに出力します。この面積は、 the Polygon Area (polyarea) X-Function によって計算されます。Polygon Area は同じZ値の等高線で囲まれた面積を返します。等高線に囲まれた面積の減算はありません。
等高線データを抽出するには:
- 1回 クリックすると、全ての等高線が選択されます。
- 2回クリックすると、同じZ値にある全ての等高線が選択されます。
- 3回目のクリックでは、1つの等高線が選択されます。
選択した等高線で右クリックし、 等高線データの抽出 を選択します。等高線面積を含む等高線データが、新規のブックに出力されます。
ワークシートから等高線を作成するアルゴリズム
等高線図は、グリッディングせずに (x, y, z) 座標(直交座標)または (r, 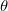 , z) 座標(極座標)から直接作成することができます。 データが (r, , z) 座標(極座標)から直接作成することができます。 データが (r, 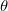 , z) 座標にある場合、Originは、まず、等高線を作成する前にデータをXYZ空間に変換します。(x, y, z)座標 と (r, , z) 座標にある場合、Originは、まず、等高線を作成する前にデータをXYZ空間に変換します。(x, y, z)座標 と (r, 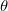 , z) 座標の変換は、次式で行われます。 , z) 座標の変換は、次式で行われます。
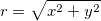
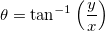

さらに
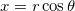
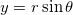

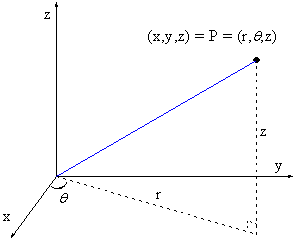
直交座標では、4つのステップで等高線を作成します。
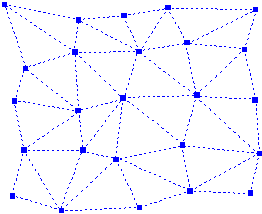
三角分割
すべてのデータポイントは接続され、XY平面上でティーセン(ドロネー)の三角形を作成します。三角形は可能な限り等角になるように作成されます。さらに、2つの三角形が交わることはありません。 三角形の辺がメッシュの端でなければ、それは2つの三角形で共有されます。
線形補間
等高線と三角形の辺の交点を見つけるために線形補間が行われます。
等高線レベルzcを指定すると、Originは、すべての三角形を横断し、このレベルの等高線が三角形と交わるかどうかを調べます。三角形の一辺が、等高線と交わると、それが指標の辺として印が付けられます。そして、交点の座標は、この文書内で指標の点として参照され、線形補間で計算されます。
三角形の2つの頂点 I(xi, yi, zi) と J(xj, yj, zj)を結ぶ三角形の辺に対して、以下のことが真であるかどうかを調べます。
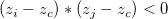
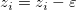
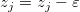
真の場合、この辺が指標の辺であるということができます。 さらに、不等式の左側の積が0の場合、等高線が少なくとも頂点の1つを通るということになります。この場合、zi と zj は、小さな値 を減算することによって調整され、指標の点は頂点ではなくなります。調整は以下のように行われます。 を減算することによって調整され、指標の点は頂点ではなくなります。調整は以下のように行われます。
ここで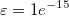 です。 です。
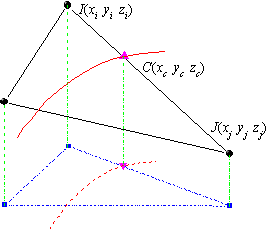
この辺が指標の辺の場合、その上にある指標の点の座標は次の方法で線形補間され計算されます。
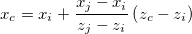
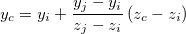
Originは、今後利用するために、すべての指標の辺と指標の点の座標を記録します。
三角形が等高線と交わる場合、2つの指標の辺があるということです。
等高線の描画
等高線を描画するには、その上にすべての指標の点をトレースする必要があります。
三角メッシュの境界線上に指標の点がある場合、その点からトレースを開始します。 それ以外の場合、いずれかの指標の点からトレースを開始します。
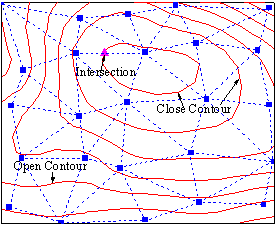
等高線で遮断する三角形は2つの指標の辺を持ち、メッシュの端にない辺は2つの三角形で共有されなければならないことを思い出して下さい。したがって、ある指標の一辺(次の図でSide A)から同じ三角形の別の指標の辺(次の図でSide B)にトレースすることができます。後者が、三角メッシュの端にない場合、現在の三角形 (次の図のTriangle 1)でこの辺を共有する別の三角形(次の図のTriangle 2)を見つけます。そして、この新しい三角形の別の辺(次の図でSide C)の指標の点を見つけることができます。 このようにして、メッシュの端または既にトレースを行った指標の点に達するまで、トレースを続けます。(前者の場合、等高線は閉じませんが、後者の場合、等高線は閉じます。)トレースされる指標の点の数がこのレベルでの指標の点の合計数と比較されます。 それらが等しくない場合、いくつかの指標の点がトレースされていないということになります。 すべての指標の点がトレースされるまでトレースが続きます。
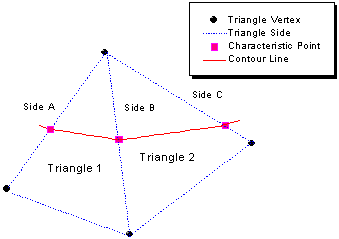
接続とスムージング
トレースが終わったら、指標の点が直線で接続されます。スムージングは、作図の詳細ダイアログの等高線設定でスムージングのチェックが付いているワークシートからの等高線図で利用可能です。スムージングパラメータや、ワークシートから作成された等高線図に使用される TPSアルゴリズムについての情報を確認してください。
行列から等高線を作成するアルゴリズム
行列(または仮想行列)から等高線図を作図する際も同様ですが、アルゴリズムはよりシンプルで、次の3つのステップで行われます。
線形補間において、等高線の描画は、ワークブックから等高線図を作図するのと同じアルゴリズムが使用されます。
行列から作成される等高線図の線の接続では、直線で特性点を結びます。後にスムージングは実行されません。
参考
- Robert J. Renka.Interpolation of Data on the Surface of a Sphere.ACM Transactions on Mathematical Software, Vol. 10, No. 4, December 1984, Pages 417-436.
- Fen Yuan, Automatic Drawing of Equal Quantity Curve.Computer Aided Engineering, No. 3 Sept. 1998.
|