ランダム配置データのグリッディング法GridMethod-RandomSpaced
ワークシートデータがXおよびY方向に等間隔に並んでいない場合、ランダムまたは等間隔でないXYデータに対するOriginの5つのグリッディング手法の1つを使います。
Renka- Cline法
このグリッディング法は、1984年にRenka と Clineによって開発されたアルゴリズムに基づいています。このアルゴリズムの主要な計算は次のように行われます。
- 三角分割XYデータに対して三角分割法が実行されます。三角形は可能なかぎりほぼ等角になります。
- 傾斜推定二次関数の偏微分として、各格子におけるxy方向の傾斜を推定します。
- 補間任意の点 Pにおいて、データ値を使って補間された値と点Pを含む三角形の3つの頂点のそれぞれの位置での傾斜推定を計算します。
200~1000程度のデータポイントが一様に分布している場合には、Renka-Cline法は良い選択肢となります。
Shepard法
この手法は、Franke と Nielsonによって開発された修正Shepardグリッディング法を組み込んだものです。これは、次の式でデータを補間する、距離で重み付けしたグリッディング法です。
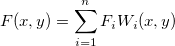
ここで 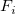 は、ノード ( は、ノード (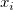 , , 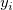 ) における基本関数で、 ) における基本関数で、 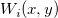 は重み付けです。計算を制限するため、 は重み付けです。計算を制限するため、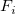 と と 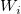 は円の中心( は円の中心(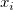 , , 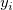 )で半径が )で半径が 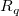 および および 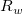 を持つ円の中にあるデータポイントで計算されます。 を持つ円の中にあるデータポイントで計算されます。
次の式で定義される重み付けで開始します。
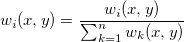 . .
半径 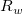 を与えると、その相対的な重み付け を与えると、その相対的な重み付け 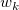 は、 は、
![w_k=[\frac{(R_w-d_k)_{+}}{R_wd_k}]^2 w_k=[\frac{(R_w-d_k)_{+}}{R_wd_k}]^2](//d2mvzyuse3lwjc.cloudfront.net/doc/ja/UserGuide/images/Gridding_Methods_for_Randomly_Spaced_Data/math-0e141a3a2c838ddf192009baaf5116ad.png) ここで、 ここで、
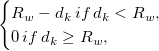
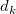 は (x, y) と( は (x, y) と(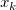 , , 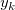 )間の距離です。 )間の距離です。
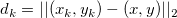 . .
どの 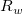 >0においても、次のようになります。 >0においても、次のようになります。
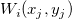 = =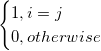
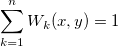 . .
次に、 節点関数 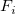 が局所的な近似関数 が局所的な近似関数 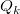 に置き換えられます。 に置き換えられます。
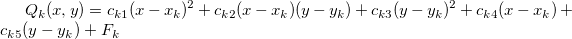
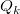 は、節点の は、節点の 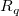 範囲内にあるデータに重み付けされた最小二乗二次フィット関数です。そして、係数は次の式を最小化するものです。 範囲内にあるデータに重み付けされた最小二乗二次フィット関数です。そして、係数は次の式を最小化するものです。
![\varepsilon _k=\sum_{i=1,j\neq k}^N\omega _i(x_k,y_k)[c_{k1}(x_i-x_k)^2+\ldots +c_{k5}(y_i-y_k)+F_k-F_i]^2 \varepsilon _k=\sum_{i=1,j\neq k}^N\omega _i(x_k,y_k)[c_{k1}(x_i-x_k)^2+\ldots +c_{k5}(y_i-y_k)+F_k-F_i]^2](//d2mvzyuse3lwjc.cloudfront.net/doc/ja/UserGuide/images/Gridding_Methods_for_Randomly_Spaced_Data/math-8ab8ecc395dfc1db378345af3deb4929.png)
ここで
![\omega _i(x,y)=[\frac{(R_q-d_i)_{+}}{R_qd_i}]^2=[\frac{(R_q-||(x_i,y_i)-(x,y)||_2)_{+}}{R_q||(x_i,y_i)-(x,y)||_2}]^2 \omega _i(x,y)=[\frac{(R_q-d_i)_{+}}{R_qd_i}]^2=[\frac{(R_q-||(x_i,y_i)-(x,y)||_2)_{+}}{R_q||(x_i,y_i)-(x,y)||_2}]^2](//d2mvzyuse3lwjc.cloudfront.net/doc/ja/UserGuide/images/Gridding_Methods_for_Randomly_Spaced_Data/math-82914bba8b91c96a6d5fe1c5865f7fe6.png) . .
上記で補間関数は、局所近似関数であり、格子ポイント 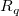 および および 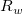 での影響半径に依存すると考えることができます。2つの整数 での影響半径に依存すると考えることができます。2つの整数 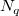 と と 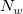 が、 が、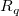 と と 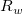 を計算するのに使われます。(これらは、関数のパラメータ q と w であり、それぞれ二次補間局所因子と重み関数局所因子です詳細は、このセクションの『XYZグリッディングダイアログボックス』をご覧ください。) を計算するのに使われます。(これらは、関数のパラメータ q と w であり、それぞれ二次補間局所因子と重み関数局所因子です詳細は、このセクションの『XYZグリッディングダイアログボックス』をご覧ください。)
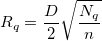 および および 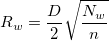
ここで n はデータポイントの数で、 D は一対のデータポイント間の距離の最大です。そのため、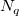 と と 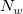 は、それぞれ各格子において、距離 は、それぞれ各格子において、距離 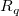 および および 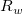 の範囲内にあるデータポイントの平均の数だと考えることができます。 の範囲内にあるデータポイントの平均の数だと考えることができます。
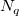 と と 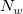 の値を増加させると、計算が全体に及ぶようになり、同様にこれらの値を減少させると、計算が局所的になります。 一般に、 の値を増加させると、計算が全体に及ぶようになり、同様にこれらの値を減少させると、計算が局所的になります。 一般に、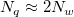 とすると良い結果が得られます。デフォルトでは とすると良い結果が得られます。デフォルトでは 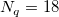 および および 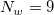 となっています。しかし、以下の制約を満たしている必要があります。 となっています。しかし、以下の制約を満たしている必要があります。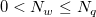 . .
「XYZグリッディング」ダイアログは、 NAG 関数ライブラリを呼び出して、Shepardグリッディング法を実行しています。また、Originは Shepardグリッディング法を行うXファンクションも提供しており、xyz_shep_nag および xyz_shepは、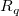 と と 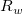 を使って、この手法を組み込んでいます。 を使って、この手法を組み込んでいます。
TPS (Thin Plate Spline)法
この関数は、TPS(Thin Plate Spline)アルゴリズムを使って、ランダム配置データの行列変換を行う手法を提供しています。TPS法は、物理的な補間の方法です。グリッディングデータを生成するため、この方法では、すべてのデータポイントが薄い弾性プレートまたはスプライン上に分布しているものと仮定します。プレートはグリッド点に制限され、グリッド点を結ぶことで、2次元の曲面を形成します。曲面は、データポイントに合うように形成するために点と点の間で変形します。最適な結果は、通常、スプラインの「曲げエネルギー関数」を最小化することで見つかります。
この手法は、曲げエネルギーの最小値を見つけるので、プレートの変形を最小に抑え、より良い結果が得られます。この計算は、曲率計算を最小化するのにも似ています。TPSグリッディング法を使った曲面プロットは、他の手法よりも滑らかになりますので、この手法は、局所的に平坦な曲面の補間に対して適しています。
TPSアルゴリズムの数学的な説明としては、次の曲げエネルギー関数が与えられ
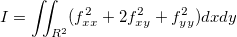
そして、最小化される関数は
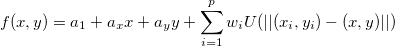
ここで、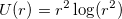 です。 です。
TPSグリッディングを実行するには、スムージングのパラメータと補外パラメータを指定する必要があり、スムージングのパラメータは補間した曲面の滑らかさを制御し、 補外パラメータは、元のデータの範囲を超えて行列のセルにデータを入力するのに使用されます。
TPSアルゴリズムについての詳細は、参考文献『Donato and Belongie, Approximation Methods for Thin Plate Spline Mappings and Principal Warps』をご覧下さい。
Kriging相関法
Kriging法(鉱山工学者の D. G Krigeの名前から付けられた)は、空間データを補間するのに、よく知られている地理統計学の手法です。この手法は、重み付けした隣接平均により、計算したい位置(グリッド点)での推定した分散を最小化する重み付け移動平均補間(補外)法です。そして、重み付けした値は元データの空間的な相関構造で決定します。
このアルゴリズムは、空間の連続性または従属性のモデルが必要です。通常、処理を2つに分けることができます。
- 計算したい領域毎に分けた変数の半分散図を作成します。Originは距離の情報を計算し、半分散値に変換して表に保存し、半分散値に重みを付けます。この半分散図は、入力データセットでの標本間の差の増分や相関の減少を説明するものです。
- この従属モデルを使って、z値の空間ポイントの値を計算します。
Kriging相関法を実行するとき、次のパラメータを使って処理を制御することができます。
- 最小ポイント: Zの計算に必要な最小の制御ポイントの数をセットします。
- 検索半径:どれだけ離れたポイントをZの計算対象にするかを指定します。
Kriging法についての詳細は、参考文献『Stein, Interpolation of Spatial Data』をご覧ください。
加重平均
加重平均法は、1/rの重み付けを持つポイントの単純な加重平均で、rは、検索半径の範囲内にあるセルからの各ポイントの距離です。検索半径の範囲内に値が無い場合、少なくとも1ポイント出現するまで半径を拡大します。検索半径を拡大するということは、各ポイントは隣り合うポイントとの内部的な関係を強め、詳細な部分を失って、より滑らかな曲面を作成するということになります。
|