Algorithmen (Lineare Anpassung mit X-Fehler)
Ref-Linear-XErr
Das Anpassungsmodell
Für einen gegebenen Datensatz 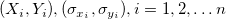 , wobei X die unabhängige Variable und Y die abhängige Variable ist, und , wobei X die unabhängige Variable und Y die abhängige Variable ist, und 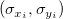 Fehler für X bzw. Y sind. -- Lineare Anpassung X-Fehler passt die Daten an ein Modell mit der folgenden Form an: Fehler für X bzw. Y sind. -- Lineare Anpassung X-Fehler passt die Daten an ein Modell mit der folgenden Form an:
Fit-Steuerung
Berechnungsmethode
-
York-Methode
- Die York-Methode Verwendet die Berechnungsmethode von D. York, beschrieben in Vereinte Gleichungen für Steigung, Schnittpunkt mit der Y-Achse und Standardfehler der besten geraden Linie
-
FV-Methode
- Die FV-Methode ist die Berechnungsmethode von Giovanni Fasano & Roberto Vio, beschrieben in Eine gerade Linie mit Fehler an beiden Koordinaten anpassen.
-
Deming-Methode
- Die Deming-Regression ist die Maximum-Likelihood-Schätzung eines Fehler-in-Variablen-Modell. Von den X/Y-Fehlern wird angenommen, dass sie unabhängig identisch verteilt sind.
-
Korrelation zwischen X- und Y-Fehlern
- Korrelation zwischen X- und Y-Fehlern
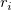 (nur für York-Methode) (nur für York-Methode)
-
Standardabweichung von X/Y
- Standardabweichung von X/Y (nur für Deming-Methode)
Eigenschaften (York-Methode)
Wenn Sie eine lineare Anpassung durchführen, erstellen Sie ein Analyseberichtsblatt, dass die berechneten Eigenschaften enthält. Die Tabellenberichte Parameter modellieren Steigung und Schnittpunkt mit der Y-Achse (Zahlen in Klammern zeigen, wie die Eigenschaften abgeleitet werden):
Fit-Parameter

Angepasster Wert und Standardfehler
Definieren Sie 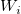 , das die Gewichtung (Fehler) für X und Y beinhaltet; , das die Gewichtung (Fehler) für X und Y beinhaltet;
Darin sind 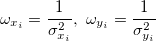 Gewichtungen von Gewichtungen von 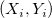 , , 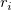 ist die Korrelation zwischen X- und Y-Fehler (d. h. ist die Korrelation zwischen X- und Y-Fehler (d. h. 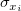 und und 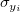 ), und ), und 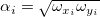 . .
Die Steigung der angepassten Linie für 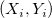 ohne Gewichtung (Fehler) ist der Initialisierungswert für ohne Gewichtung (Fehler) ist der Initialisierungswert für 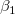 . Sie sollten iterativ gelöst werden, bis sukzessive Schätzungen von . Sie sollten iterativ gelöst werden, bis sukzessive Schätzungen von 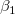 innerhalb der gewünschten Toleranz übereinstimmen. innerhalb der gewünschten Toleranz übereinstimmen.
Die präzisen Gleichungen, die die Parameter 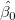 und und 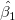 für die am besten angepasste Linie mit X-Y-Fehlern schätzen, sind: für die am besten angepasste Linie mit X-Y-Fehlern schätzen, sind:
wobei 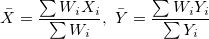 . .
U und V sind die Abweichung für X und Y:
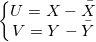
und
Die entsprechende Variation 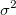 und der Standardfehler und der Standardfehler  für Parameter sind: für Parameter sind:
wobei 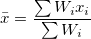 , , 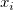 ist der erwartete Wert von ist der erwartete Wert von 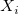 , und , und 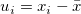 . .
Der Standardfehler für Parameter ist am Ende gegeben mit:
wobei 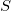 : :
t-Wert und Konfidenzniveau
Gelten die Regressionsannahmen, haben wir:
Die t-Tests können verwendet werden, um zu untersuchen, ob die Fit-Parameter signifikant von Null abweichen. Das bedeutet, wir können testen, ob 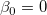 (falls wahr, bedeutet dies, dass die angepasste Linie durch den Ursprung verläuft) oder (falls wahr, bedeutet dies, dass die angepasste Linie durch den Ursprung verläuft) oder 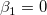 . Die Hypothesen der t-Tests sind: . Die Hypothesen der t-Tests sind:
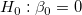 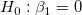 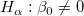 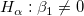
Die t-Werte können wie folgt berechnet werden:
Mit dem berechneten t-Wert können wir entscheiden, ob die entsprechende Nullhypothese verworfen werden soll oder nicht. Gewöhnlich können wir für ein gegebenes Konfidenzintervall  die Hypothese die Hypothese 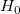 verwerfen, wenn verwerfen, wenn 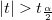 . Außerdem wird der p-Wert oder die Signifikanzebene mit einem t-Test angezeigt. Wir weisen auch die Nullhypothese . Außerdem wird der p-Wert oder die Signifikanzebene mit einem t-Test angezeigt. Wir weisen auch die Nullhypothese 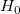 zurück, wenn der p-Wert kleiner ist als zurück, wenn der p-Wert kleiner ist als  . .
Wahrsch.>|t|
Die Wahrscheinlichkeit, dass 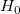 in dem t-Test oben wahr ist. in dem t-Test oben wahr ist.
wobei tcdf(t, df) die untere Wahrscheinlichkeit für die studentisierte t-Verteilung mit dem df-Freiheitsgrad berechnet.
UEG und OEG
Mit dem t-Wert können wir das 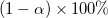 -Konfidenzintervall für jeden Parameter berechnen: -Konfidenzintervall für jeden Parameter berechnen:
wobei 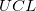 und und 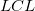 für Oberes Konfidenzintervall bzw. Unteres Konfidenzintervall steht. für Oberes Konfidenzintervall bzw. Unteres Konfidenzintervall steht.
KI halbe Breite
Das Konfidenzintervall halbe Breite ist:
wobei OEG und UEG das obere Konfidenzintervall bzw. untere Konfidenzintervall ist.
Weitere Informationen finden Sie in der Referenz 1 (unten).
Statistik zum Fit
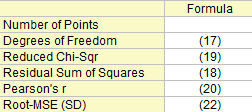
Freiheitsgrade
n ist die Gesamtanzahl der Punkte.
Summe der Fehlerquadrate
Reduziertes Chi-Quadrat
Pearson r
Bei der einfachen linearen Regression ist der Korrelationskoeffizient zwischen x und y, der als r bezeichnet wird, gleich:
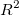 kann berechnet werden mit: kann berechnet werden mit:
Wurzel-MSE (StAbw)
Quadratwurzel des Mittelwerts des Fehlers oder die residuale Standardabweichung ist gleich:
Kovarianz- und Korrelationsmatrix
Die Kovarianzmatrix der linearen Regression wird berechnet durch:
Die Korrelation zwischen zwei beliebigen Parametern ist:
Eigenschaften (FV-Methode)
Die FV-Methode ist die Berechnungsmethode von Giovanni Fasano & Roberto Vio, beschrieben in Eine gerade Linie mit Fehler an beiden Koordinaten anpassen.
Die Gewichtung wird definiert als:
Die Steigung der angepassten Linie für 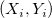 ohne Gewichtung (Fehler) ist ohne Gewichtung (Fehler) ist 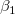 . .
Es wird angenommen, dass
indem die Summe 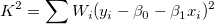 minimiert wird, erhalten wir den Schätzwert minimiert wird, erhalten wir den Schätzwert 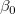 und und 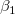 , indem die teilweisen Ableitungen auf 0 gesetzt werden. , indem die teilweisen Ableitungen auf 0 gesetzt werden.
wobei
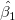 sollte iterativ gelöst werden, bis sukzessive Schätzungen von sollte iterativ gelöst werden, bis sukzessive Schätzungen von 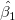 innerhalb der gewünschten Toleranz übereinstimmen. innerhalb der gewünschten Toleranz übereinstimmen.
Greifen Sie für jeden Parameterstandardfehler auf das lineare Regressionsmodell zurück.
Weitere Informationen finden Sie in der Referenz 2 (unten).
Eigenschaften (Deming-Methode)
Wenn Sie eine lineare Anpassung durchführen, erstellen Sie ein Analyseberichtsblatt, dass die berechneten Eigenschaften enthält. Die Tabellenberichte Parameter modellieren Steigung und Schnittpunkt mit der Y-Achse (Zahlen in Klammern zeigen, wie die Eigenschaften abgeleitet werden):
Fit-Parameter

Die Deming-Regression wird für Situationen verwendet, in denen sowohl X als auch Y einem Messungsfehler unterliegen.
Angenommen, 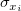 sind unabhängig identisch verteilt mit sind unabhängig identisch verteilt mit 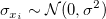 und und 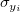 sind unabhängig verteilt mit sind unabhängig verteilt mit 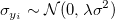 , wobei , wobei 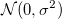 die Normalverteilung mit dem Mittelwert 0 und der Standardabweichung die Normalverteilung mit dem Mittelwert 0 und der Standardabweichung  bezeichnet. Wenn bezeichnet. Wenn 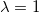 , dann ist es eine orthogonale Regression. Der gewichtete Fehler der Quadratsumme des Modells wird minimiert: , dann ist es eine orthogonale Regression. Der gewichtete Fehler der Quadratsumme des Modells wird minimiert:
Angepasster Wert und Standardfehler
Wir können Parameter lösen:
wobei:
und:
Die entsprechende Variation für Parameter ist:
Der Standardfehler für Parameter kann geschätzt werden mit:
und
t-Wert und Konfidenzniveau
Gelten die Regressionsannahmen, haben wir:
Die t-Tests können verwendet werden, um zu untersuchen, ob die Fit-Parameter signifikant von Null abweichen. Das bedeutet, wir können testen, ob 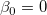 (falls wahr, bedeutet dies, dass die angepasste Linie durch den Ursprung verläuft) oder (falls wahr, bedeutet dies, dass die angepasste Linie durch den Ursprung verläuft) oder 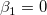 . Die Hypothesen der t-Tests sind: . Die Hypothesen der t-Tests sind:
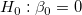 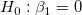 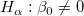 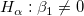
Die t-Werte können wie folgt berechnet werden:
Mit dem berechneten t-Wert können wir entscheiden, ob die entsprechende Nullhypothese verworfen werden soll oder nicht. Gewöhnlich können wir für ein gegebenes Konfidenzintervall  die Hypothese die Hypothese 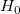 verwerfen, wenn verwerfen, wenn 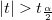 . Außerdem wird der p-Wert oder die Signifikanzebene mit einem t-Test angezeigt. Wir weisen auch die Nullhypothese . Außerdem wird der p-Wert oder die Signifikanzebene mit einem t-Test angezeigt. Wir weisen auch die Nullhypothese 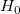 zurück, wenn der p-Wert kleiner ist als zurück, wenn der p-Wert kleiner ist als  . .
Wahrsch.>|t|
Die Wahrscheinlichkeit, dass 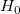 in dem t-Test oben wahr ist. in dem t-Test oben wahr ist.
wobei tcdf(t, df) die untere Wahrscheinlichkeit für die studentisierte t-Verteilung mit dem df-Freiheitsgrad berechnet.
UEG und OEG
Mit dem t-Wert können wir das 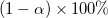 -Konfidenzintervall für jeden Parameter berechnen: -Konfidenzintervall für jeden Parameter berechnen:
wobei 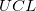 und und 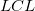 für Oberes Konfidenzintervall bzw. Unteres Konfidenzintervall steht. für Oberes Konfidenzintervall bzw. Unteres Konfidenzintervall steht.
KI halbe Breite
Das Konfidenzintervall halbe Breite ist:
wobei OEG und UEG das obere Konfidenzintervall bzw. untere Konfidenzintervall ist.
Weitere Informationen finden Sie in der Referenz 1 (unten).
Statistik zum Fit
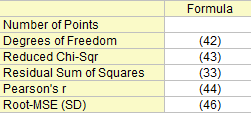
Freiheitsgrade
n ist die Gesamtanzahl der Punkte.
Summe der Fehlerquadrate
Siehe Formel (33).
Reduziertes Chi-Quadrat
Pearson r
Bei der einfachen linearen Regression ist der Korrelationskoeffizient zwischen x und y, der als r bezeichnet wird, gleich:
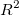 kann berechnet werden mit: kann berechnet werden mit:
Wurzel-MSE (StAbw)
Quadratwurzel des Mittelwerts des Fehlers ist gleich:
Kovarianz- und Korrelationsmatrix
Die Kovarianzmatrix der linearen Regression wird berechnet durch:
Die Korrelation zwischen zwei beliebigen Parametern ist:
Residuendiagramme
Residuen vs. Independent
Punktdiagramm der Residuen 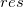 vs. unabhängige Variable vs. unabhängige Variable 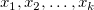 ; jede Zeichnung befindet sich in einem separaten Diagramm. ; jede Zeichnung befindet sich in einem separaten Diagramm.
Residuen vs. prognostizierte Werte
Punktdiagramm der Residuen 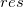 vs. Anpassungsergebnisse vs. Anpassungsergebnisse 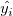
Residuen vs. die Ordnung der Datendiagramme
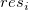 vs. Abfolgenummer vs. Abfolgenummer 
Histogramm des Residuums
Histogramm des Residuums 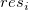
Verzögertes Residuendiagramm
Residuen 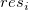 vs. verzögertes Residuum vs. verzögertes Residuum 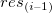
Wahrscheinlichkeitsnetz (Normal) für Residuen
Das Wahrscheinlichkeitsnetz der Residuen (Normal) kann verwendet werden, um zu prüfen, ob die Varianz ebenfalls normalverteilt ist. Wenn das sich ergebende Diagramm ungefähr linear ist, nehmen wir weiterhin an, dass die Fehlerterme normal verteilt sind. Das Diagramm basiert auf Perzentilen versus geordnete Residuen. Die Perzentile werden geschätzt mit
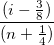
wobei n die Gesamtanzahl der Datensätze und i die i-ten Daten sind. Bitte lesen Sie auch Wahrscheinlichkeitsdiagramm und Q-Q-Diagramm.
Referenz
- York D, "Unified equations for the slope, intercept, and standard error of the best straight line", American Journal of Physics, Volume 72, Nr. 3, S. 367-375 (2004).
- G. Fasano und R. Vio, "Fitting straight lines with errors on both coordinates", Newsletter of Working Group for Modern Astronomical Methodology, Nr. 7, 2-7, Sept. 1988.
|