アルゴリズム: Xエラーあり線形フィットRef-Linear-XErr
フィッティングモデル
与えられたデータセット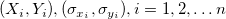 において、Xは独立変数、Yは従属変数であり、 において、Xは独立変数、Yは従属変数であり、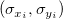 はX,Yそれぞれのエラーを表します。 Xエラー付き線形フィットは、データを次の形式のモデルに適合させます。 はX,Yそれぞれのエラーを表します。 Xエラー付き線形フィットは、データを次の形式のモデルに適合させます。
フィット制御
計算法
- York法
- York法はD.Yorkの計算法であり、最良の傾き、切片、標準偏差を持つ最善の直線について説明されています。
- FV法
- FV法はGiocanniFasano & Roberto Vioによる計算方法で、両方の座標にエラーのある直線へのフィットについて説明されています。
- Deming法
- Deming回帰は、変数内誤差モデルの最尤推定であり、X/Y 誤差は独立して等分布していると仮定されます。
- XおよびYエラーの相関
- XおよびYエラーの相関
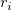 (York法のみ) (York法のみ)
- X/Yの標準偏差
- X/Yの標準偏差(Deming法のみ)
値(York法)
線形フィットを実行すると、分析レポートシートに計算された値が出力されます。 パラメータ表にはモデルの傾きと切片(カッコ内の数字は計算された値を示す)が表示されます。
フィットパラメータ

フィット値と標準誤差
xとyの重み(誤差)に関する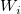 を定義します。 を定義します。
このとき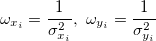 は は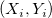 の重みで、 の重みで、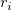 はXとYの誤差の相関係数(すなわち はXとYの誤差の相関係数(すなわち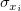 と と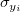 )で )で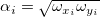 です。 です。
重みづけ(誤差)のない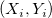 のフィット線の傾きは のフィット線の傾きは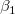 の初期値になります。設定した許容値 の初期値になります。設定した許容値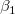 に収まるまでこれらは反復計算されます。 に収まるまでこれらは反復計算されます。
X_Y誤差のあるもっとフィットする線の推定パラメータ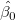 と と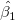 の簡潔な方程式は次のようになります。 の簡潔な方程式は次のようになります。
ここで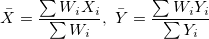 です。 です。
UとVはXとYの偏差です。
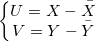
および、
パラメータの対応する変数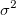 と標準誤差 と標準誤差 は次のようになります。 は次のようになります。
ここで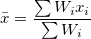 、 、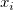 は は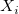 の推定値で、 の推定値で、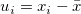 です。 です。
パラメータの標準誤差は最終的に次のようになります。
ここで は は
t値と信頼水準
回帰の仮定が成り立つ場合次のようになります。
フィッティングパラメータが0ではないことを調べるためにt 検定を使うことができます。これは、  (真ならば、フィット直線が原点を通る) または (真ならば、フィット直線が原点を通る) または 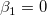 であるかどうかを検定します。t 検定の仮説検定は次のようになります。 であるかどうかを検定します。t 検定の仮説検定は次のようになります。
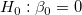 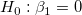 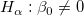 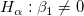
t 値は、次の式で計算できます。
計算されたt値を使って対応する帰無仮説を棄却するかどうかを決定できます。通常与えられた有意水準 に対して、 に対して、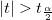 のときに のときに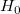 を棄却します。また、p値または有意水準がt検定とともに出力されます。p値が を棄却します。また、p値または有意水準がt検定とともに出力されます。p値が よりも小さい場合に帰無仮説 よりも小さい場合に帰無仮説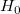 を棄却することができます。 を棄却することができます。
Prob>|t|
上記のt検定における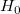 が真である確率 が真である確率
ここで、tcdf(t, df) は、自由度 df を持つスチューデントt 分布の下側の確率を計算します。
LCLとUCL
t値から各パラメータの信頼区間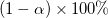 を次の式で計算できます。 を次の式で計算できます。
ここで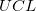 と と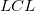 はそれぞれ上限信頼区間と下限信頼区間の略です。 はそれぞれ上限信頼区間と下限信頼区間の略です。
CI 半幅
信頼区間の半値幅は以下の通りです。
ここでUCLとLCLは、それぞれ上側信頼区間と下側信頼区間です。
より詳細は参考文献1(下記)をご覧ください。
フィット統計

自由度
nは合計ポイント数です。
残差平方和
自由度あたりカイ二乗
ピアソンのr
単純な線形回帰では、xとyの相関係数は、r で表され、次の式に等しくなります。
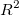 これは次式のように計算されます。 これは次式のように計算されます。
Root MSE(SD)
誤差の平均平方の平方根または、残差標準偏差は、次式に等しくなります。
共分散行列と相関行列
線形回帰における共分散行列は次のように計算されます。
2つのパラメータ間の相関は、
値 (FV法)
FV法はGiocanniFasano & Roberto Vioによる計算方法で、両方の座標にエラーのある直線へのフィットについて説明されています。
重みは次のように定義されます。
重みづけ(誤差)のない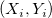 のフィット線の傾きは のフィット線の傾きは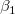 です。 です。
次のようにします。
合計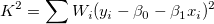 を最小化し、偏微分を0に設定することで値 を最小化し、偏微分を0に設定することで値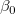 と と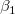 を推定することができます。 を推定することができます。
ここで
設定した許容値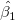 に収まるまで に収まるまで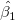 は反復計算されます。 は反復計算されます。
それぞれのパラメータの標準誤差については線形回帰モデルを参照してください。
より詳細は参考文献2(下記)をご覧ください。
5値 (Deming法)
線形フィットを実行すると、分析レポートシートに計算された値が出力されます。 パラメータ表にはモデルの傾きと切片(カッコ内の数字は計算された値を示す)が表示されます。
フィットパラメータ

Deming回帰はxとyに測定誤差あることが前提とされる場合に使われます。
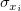 は、 は、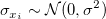 と独立で同一の分布に従い、 と独立で同一の分布に従い、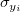 は、 は、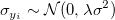 と独立で同一の分布に従うと仮定します。 ここで、 と独立で同一の分布に従うと仮定します。 ここで、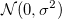 は平均0と標準偏差 は平均0と標準偏差 の正規分布を示します。 の正規分布を示します。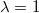 の場合それは直交回帰です。
モデルの加重残差平方和は最小化され、 の場合それは直交回帰です。
モデルの加重残差平方和は最小化され、
フィット値と標準誤差
パラメータを解くことができます。
ここで、
さらに
パラメータの対応する変数は次のようになります。
パラメータの標準誤差は次のように推定できます。
および、
t値と信頼水準
回帰の仮定が成り立つ場合次のようになります。
フィッティングパラメータが0ではないことを調べるためにt 検定を使うことができます。これは、 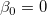 (真ならば、フィット直線が原点を通る) または (真ならば、フィット直線が原点を通る) または 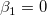 であるかどうかを検定します。t 検定の仮説検定は次のようになります。 であるかどうかを検定します。t 検定の仮説検定は次のようになります。
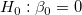 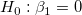 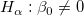 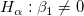
t 値は、次の式で計算できます。
計算されたt値を使って対応する帰無仮説を棄却するかどうかを決定できます。通常与えられた有意水準 に対して、 に対して、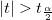 のときに のときに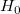 を棄却します。また、p値または有意水準がt検定とともに出力されます。p値が を棄却します。また、p値または有意水準がt検定とともに出力されます。p値が よりも小さい場合に帰無仮説 よりも小さい場合に帰無仮説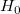 を棄却することができます。 を棄却することができます。
Prob>|t|
上記のt検定における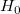 が真である確率 が真である確率
ここで、tcdf(t, df) は、自由度 df を持つスチューデントt 分布の下側の確率を計算します。
LCLとUCL
t値から各パラメータの信頼区間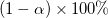 を次の式で計算できます。 を次の式で計算できます。
ここで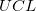 と と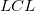 はそれぞれ上限信頼区間と下限信頼区間の略です。 はそれぞれ上限信頼区間と下限信頼区間の略です。
CI 半幅
信頼区間の半値幅は以下の通りです。
ここでUCLとLCLは、それぞれ上側信頼区間と下側信頼区間です。
より詳細は参考文献1(下記)をご覧ください。
フィット統計

自由度
nは合計ポイント数です。
残差平方和
式(33)を参照
自由度あたりカイ二乗
ピアソンのr
単純な線形回帰では、xとyの相関係数は、r で表され、次の式に等しくなります。
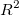 これは次式のように計算されます。 これは次式のように計算されます。
Root MSE(SD)
誤差の平均平方の平方根は、次式に等しくなります。
共分散行列と相関行列
線形回帰における共分散行列は次のように計算されます。
2つのパラメータ間の相関は、
残差プロット
残差vs.独立
残差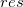 vs. 独立変数 vs. 独立変数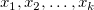 の散布図プロットではそれぞれのプロットは別々のグラフに配置されます。 の散布図プロットではそれぞれのプロットは別々のグラフに配置されます。
残差vs.予測値
残差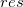 の散布図プロット vs. フィット結果 の散布図プロット vs. フィット結果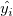
残差vs.データ順序
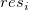 vs. 順序 vs. 順序
残差のヒストグラム
残差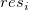 のヒストグラムプロット のヒストグラムプロット
残差のラグプロット
残差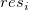 vs. ラグ残差 vs. ラグ残差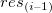
正規残差確率プロット
残差の正規確率プロットは分散が成否分布しているかどうかを調べるために使います。結果のプロットはおおよそ線形で、誤差範囲は正規分布していると仮定することができます。プロットはパーセンタイル対順序化された残差をベースにしており、パーセンタイルは次のように仮定されます。
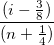
ここで、n はデータセットの合計数で、iはi番目のデータを表します。
確率プロットとQ-Qプロットもご覧ください。
参考文献
- York D, Unified equations for the slope, intercept, and standard error of the best straight line, American Journal of Physics, Volume 72, Issue 3, pp. 367-375 (2004).
- G. Fasano and R. Vio, "Fitting straight lines with errors on both coordinates", Newsletter of Working Group for Modern Astronomical Methodology, No. 7, 2-7, Sept. 1988.
|