Algorithmus (Lineare Regression)
LR-Algorithm
Das Modell der linearen Regression
Einfaches lineares Regressionsmodell
Für einen gegebenen Datensatz 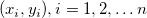 -- wobei X die unabhängige Variable und Y die abhängige Variable ist, -- wobei X die unabhängige Variable und Y die abhängige Variable ist, 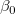 und und 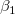 die Parameter sind, die Parameter sind, 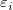 ein Zufallsfehlerterm mit Mittelwert ein Zufallsfehlerterm mit Mittelwert 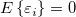 ist und die Varianz ist und die Varianz 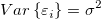 -- passt die lineare Regression die Daten an ein Modell der folgenden Form an: -- passt die lineare Regression die Daten an ein Modell der folgenden Form an:
Die Schätzung der kleinsten Quadrate wird verwendet, um die Summe von n quadrierten Abweichungen zu minimieren.
Die geschätzten Parameter des linearen Modells können folgendermaßen berechnet werden:
wobei:
und
| Hinweis: Wenn der Schnittpunkt vom Modell ausgeschlossen ist, werden die Koeffizienten mit der unkorrigierten Formel berechnet. |
Daher schätzen wir die Regressionsfunktion folgendermaßen:
Das Residuum 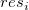 ist definiert als: ist definiert als:
Die Formel in (2) muss so minimiert werden, dass sie gleich der Summe der Fehlerquadrate ist.
wenn die Schätzung der kleinsten Quadrate 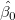 und und 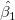 zum Schätzen von zum Schätzen von 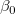 und und 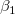 verwendet werden. verwendet werden.
Fit-Steuerung
Fehler als Gewichtung
Im obigen Abschnitt wird angenommen, dass es eine konstante Varianz in den Fehlern gibt. Wenn wir jedoch die Versuchsdaten anpassen, müssen wir vielleicht den Fehler des Instruments im Anpassungsprozess berücksichtigen (der die Genauigkeit und Präzision eines Messinstruments wiedergibt). Daher wird die Annahme der konstanten Varianz in den Fehlern verletzt. Wir müssen annehmen, dass 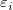 normalverteilt ist mit einer nicht konstanten Varianz und die Fehler als normalverteilt ist mit einer nicht konstanten Varianz und die Fehler als 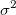 agieren, was als Gewichtung bei der Anpassung verwendet werden kann. Die Gewichtung wird definiert als: agieren, was als Gewichtung bei der Anpassung verwendet werden kann. Die Gewichtung wird definiert als:
Das Anpassungsmodell wird wie folgt geändert:
Die Gewichtungsfaktoren 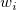 können durch drei Formeln gegeben sein: können durch drei Formeln gegeben sein:
Keine Gewichtung
Der Fehlerbalken wird in der Berechnung nicht als Gewichtung behandelt.
Direkte Gewichtung
Instrumental
Der Wert der instrumentellen Gewichtung ist antiproportional zu Instrumentenfehlern, so dass ein Versuch mit kleinen Fehlern eine große Gewichtung haben wird, da er im Vergleich zu Versuchen mit größeren Fehlern präziser ist.
| Hinweis: Die Fehler als Gewichtung sollten der Spalte "Y-Fehler" im Arbeitsblatt zugewiesen werden. |
|
Fester Schnittpunkt mit der Y-Achse (bei)
Fester Schnittpunkt mit der Y-Achse legt den Y-Schnittpunkt 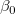 auf einen festen Wert fest, während der Gesamtfreiheitsgrad n*=n-1 ist aufgrund des festgelegten Schnittpunkts mit der Y-Achse. auf einen festen Wert fest, während der Gesamtfreiheitsgrad n*=n-1 ist aufgrund des festgelegten Schnittpunkts mit der Y-Achse.
Skalierungsfehler mit Quadrat (Reduziertes Chi-Quadrat)
Die Option Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) ist verfügbar, wenn mit Gewichtung angepasst wird. Diese Option beeinflusst nur den Fehler auf die Parameter, die der Anpassungsprozess meldet, und nicht den Anpassungsprozess selbst oder die Daten in irgendeiner Weise. Die Option ist standardmäßig aktiviert, und 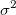 wird zum Berechnen der Fehler auf die Parameter berücksichtigt. Ansonsten wird die Varianz von wird zum Berechnen der Fehler auf die Parameter berücksichtigt. Ansonsten wird die Varianz von 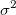 nicht zur Fehlerberechnung berücksichtigt. Nehmen Sie die Kovarianzmatrix als ein Beispiel: Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) verwenden: nicht zur Fehlerberechnung berücksichtigt. Nehmen Sie die Kovarianzmatrix als ein Beispiel: Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) verwenden:
Keinen Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) verwenden:
Für die gewichtete Anpassung wird 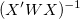 anstatt anstatt 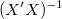 verwendet. verwendet.
Fit-Ergebnisse
Wenn Sie eine lineare Anpassung durchführen, erstellen Sie ein Analyseberichtsblatt, dass die berechneten Eigenschaften enthält. Die Tabellenberichte Parameter modellieren Steigung und Schnittpunkt mit der Y-Achse (Zahlen in Klammern zeigen, wie die Eigenschaften abgeleitet werden):
Fit-Parameter

Angepasster Wert
Siehe Formel (3)&(4).
Die Parameterstandardfehler
Für jeden Parameter kann der Standardfehler, wie folgt, ermittelt werden:
wobei die Beispielvarianz 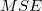 (oder Quadrat des Mittelwertfehlers (oder Quadrat des Mittelwertfehlers 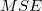 ) folgendermaßen geschätzt werden kann: ) folgendermaßen geschätzt werden kann:
RSS steht für die Residuensumme des Quadrats (oder Fehlersumme des Quadrats, SSE), die tatsächlich die Summe der Quadrate der vertikalen Abweichungen von jedem Datenpunkt aus zur angepassten Linie darstellt. Es kann wie folgt berechnet werden:
Hinweis: Im Bezug auf 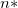 , wenn der Schnittpunkt mit der Y-Achse in dem Modell enthalten ist, ist , wenn der Schnittpunkt mit der Y-Achse in dem Modell enthalten ist, ist 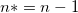 . Ansonsten . Ansonsten 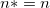 . . |
t-Wert und Konfidenzniveau
Gelten die Regressionsannahmen, haben wir:
Die t-Tests können verwendet werden, um zu untersuchen, ob die Fit-Parameter signifikant von Null abweichen. Das bedeutet, wir können testen, ob 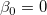 (falls wahr, bedeutet dies, dass die angepasste Linie durch den Ursprung verläuft) oder (falls wahr, bedeutet dies, dass die angepasste Linie durch den Ursprung verläuft) oder 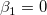 . Die Hypothesen der t-Tests sind: . Die Hypothesen der t-Tests sind:
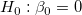 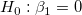 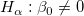 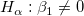
Die t-Werte können wie folgt berechnet werden:
Mit dem berechneten t-Wert können wir entscheiden, ob die entsprechende Nullhypothese verworfen werden soll oder nicht. Gewöhnlich können wir für ein gegebenes Konfidenzintervall  die Hypothese die Hypothese 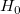 verwerfen, wenn verwerfen, wenn 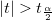 . Außerdem wird der p-Wert oder die Signifikanzebene mit einem t-Test angezeigt. Wir weisen auch die Nullhypothese . Außerdem wird der p-Wert oder die Signifikanzebene mit einem t-Test angezeigt. Wir weisen auch die Nullhypothese 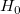 zurück, wenn der p-Wert kleiner ist als zurück, wenn der p-Wert kleiner ist als  . .
Wahrsch.>|t|
Die Wahrscheinlichkeit, dass 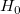 in dem t-Test oben wahr ist. in dem t-Test oben wahr ist.
wobei tcdf(t, df) die untere Wahrscheinlichkeit für die studentisierte t-Verteilung mit dem df-Freiheitsgrad berechnet.
UEG und OEG
Mit dem t-Wert können wir das 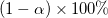 -Konfidenzintervall für jeden Parameter berechnen: -Konfidenzintervall für jeden Parameter berechnen:
wobei 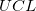 und und  für Oberes Konfidenzintervall bzw. Unteres Konfidenzintervall steht. für Oberes Konfidenzintervall bzw. Unteres Konfidenzintervall steht.
KI halbe Breite
Das Konfidenzintervall halbe Breite ist:
wobei OEG und UEG das obere Konfidenzintervall bzw. untere Konfidenzintervall ist.
Statistik zum Fit
Die Schlüsselwerte der linearen Anpassung werden in der Statistiktabelle zusammengefasst (Zahlen in Klammern zeigen, wie Eigenschaften berechnet werden):
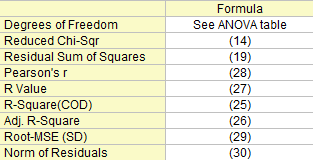
Freiheitsgrade
Der Freiheitsgrad des Fehlers Weitere Einzelheiten finden Sie in der ANOVA-Tabelle.
Summe der Fehlerquadrate
Die Residuensumme der Quadrate, siehe Formel (19).
Reduziertes Chi-Quadrat
Siehe Formel (14).
R-Quadrat (COD)
Die Qualität der linearen Regression kann mit dem Determinationskoeffizienten (COD) oder 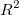 gemessen werden, die folgendermaßen berechnet werden können: gemessen werden, die folgendermaßen berechnet werden können:
wobei TSS die Gesamtsumme der Quadrate und RSS die Residuensumme des Quadrats ist. 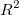 ist ein Wert zwischen 0 und 1. Liegt er nahe 1, wird die Beziehung zwischen X und Y als stark betrachtet, und wir können einen höheren Konfidenzgrad in unserem Regressionsmodell haben. ist ein Wert zwischen 0 und 1. Liegt er nahe 1, wird die Beziehung zwischen X und Y als stark betrachtet, und wir können einen höheren Konfidenzgrad in unserem Regressionsmodell haben.
Kor. R-Quadrat
Des Weiteren können wir den korrigierten 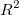 wie folgt berechnen: wie folgt berechnen:
R-Wert
Der R-Wert ist die Quadratwurzel von 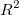 : :
Pearson r
Bei der einfachen linearen Regression ist der Korrelationskoeffizient zwischen x und y, der als r bezeichnet wird, gleich:
Wurzel-MSE (StAbw)
Quadratwurzel des Mittelwerts des Fehlers oder die residuale Standardabweichung ist gleich:
Betrag der Residuen
Ist gleich der Quadratwurzel von RSS:
ANOVA-Tabelle
Die ANOVA-Tabelle der linearen Anpassung ist:
|
Freiheitsgrade |
Summe der Quadrate |
Mittelwert der Quadrate |
F -Wert |
Wahrsch. > F |
| Modell |
1 |
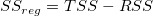 |
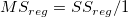 |
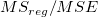 |
p-Wert |
| Fehler |
n* - 1 |
RSS |
MSE = RSS / (n* - 1) |
|
|
| Gesamt |
n* |
TSS |
|
|
|
Hinweis: Ist der Schnittpunkt im Modell enthalten, ist n*=n-1. Andernfalls ist n*=n und die Gesamtsumme der Quadrate ist unkorrigiert. Wenn die Steigung fest ist, ist 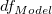 = 0. = 0. |
Dabei ist hier die Gesamtsumme der Quadrate, TSS:
Der F-Wert ist ein Test, ob das Anpassungsmodell sich signifikant von dem Modell Y = konstant unterscheidet.
Der p-Wert bzw. die Signifikanzebene wird mit einem F-Test ermittelt. Wenn der p-Wert kleiner als  ist, unterscheidet sich das Anpassungsmodell signifikant von dem Modell Y = konstant. ist, unterscheidet sich das Anpassungsmodell signifikant von dem Modell Y = konstant.
Wenn der Schnittpunkt mit der Y-Achse bei einem bestimmten Wert festgelegt wird, ist der p-Wert für den F-Test nicht bedeutungsvoll und unterscheidet sich von dem in der linearen Regression ohne die Nebenbedingung des Schnittpunkts mit der Y-Achse.
Tabelle des Tests auf fehlende Anpassung
Um den Test auf fehlende Anpassung auszuführen, müssen Sie sich wiederholende Beobachtungen zur Verfügung haben, d. h. "replizierte Daten" , so dass mindestens einer der X-Werte sich innerhalb des Datensatzes oder innerhalb mehrerer Datensätze wiederholt, wenn der Modus Zusammengefasster Fit ausgewählt ist.
Notationen, die für die Anpassung mit replizierten Daten verwenden werden:
Die Summe der Quadrate in der Tabelle unten wird ausgedrückt mit:
Die Tabelle des Tests auf fehlende Anpassung der linearen Anpassung ist:
|
Freiheitsgrade |
Summe der Quadrate |
Mittelwert der Quadrate |
F -Wert |
Wahrsch. > F |
| Fehlende Anpassung |
c-2 |
LFSS |
MSLF = LFSS / (c - 2) |
MSLF / MSPE |
p-Wert |
| Reiner Fehler |
n - c |
PESS |
MSPE = PESS / (n - c) |
|
|
| Fehler |
n*-1 |
RSS |
|
|
|
Hinweis:
Wenn der Schnittpunkt mit der Y-Achse im Modell enthalten ist, dann ist n*=n-1. Andernfalls ist n*=n und die Gesamtsumme der Quadrate ist unkorrigiert. Wenn die Steigung fest ist, ist 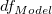 = 0. = 0.
c bezeichnet die Anzahl der eindeutigen X-Werte. Wenn der Schnittpunkt mit der Y-Achse festgelegt ist, ist der Freiheitsgrad für die fehlende Anpassung c-1.
|
Kovarianz- und Korrelationsmatrix
Die Kovarianzmatrix der linearen Regression wird berechnet durch:
Die Korrelation zwischen zwei beliebigen Parametern ist:
Ausreißer
Die Ausreißer sind die Punkte, deren absolute Werte im studentisierten Residuendiagramm größer als 2 sind.
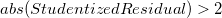
Studentisiertes Residuum wird in Ausreißer durch Transformieren der Residuen erkennen eingeführt.
Residuenanalyse
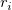 steht für reguläres Residuum steht für reguläres Residuum 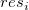 . .
Standardisiert
Studentisiert
Sind auch bekannt als intern studentisierte Residuen.
Studentisiert gelöscht
Sind auch bekannt als extern studentisierte Residuen.
In den Gleichungen der studentisierten und studentisiert gelöschten Residuen ist 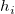 das i-te diagonale Element der Matrix das i-te diagonale Element der Matrix 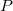 : :
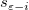 bedeutet die Varianz wird berechnet, basierend auf alle Punkte, schließt aber den iten Punkt aus. bedeutet die Varianz wird berechnet, basierend auf alle Punkte, schließt aber den iten Punkt aus.
Konfidenz- und Prognosebänder
Für einen bestimmten Wert 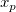 liegt das liegt das 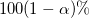 -Konfidenzintervall für den Mittelwert von -Konfidenzintervall für den Mittelwert von 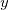 bei bei 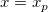 : :
Und das 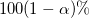 -Prognoseintervall für den Mittelwert von -Prognoseintervall für den Mittelwert von 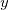 bei bei 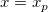 ist: ist:
Konfidenzellipsen
Angenommen das Variablenpaar (X, Y) folgt einer zweidimensionalen Normalverteilung, so können wir die Korrelation zwischen zwei Variablen durch eine Konfidenzellipse untersuchen. Die Konfidenzellipse ist bei (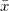 , ,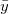 ) zentriert und die große Halbachse a und die kleine Halbachse b können folgendermaßen ausgedrückt werden: ) zentriert und die große Halbachse a und die kleine Halbachse b können folgendermaßen ausgedrückt werden:
Für ein gegebenes Konfidenzniveau von 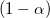 : :
- Die Konfidenzellipse für die Grundgesamtheit Mittelwert wird definiert als:
- Die Konfidenzellipse für Prognose wird definiert als:
- Der Neigungswinkel der Ellipse wird definiert als:
Residuendiagramme
Residuentyp
Wählen Sie einen Residuentyp unter Regulär, Standardisiert, Studentisiert, Studentisiert gelöscht für die Diagramme.
Residuen vs. Unabhängig
Punktdiagramm der Residuen 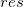 vs. unabhängige Variable vs. unabhängige Variable 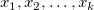 ; jede Zeichnung befindet sich in einem separaten Diagramm. ; jede Zeichnung befindet sich in einem separaten Diagramm.
Residuen vs. prognostizierte Werte
Punktdiagramm der Residuen 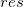 vs. Anpassungsergebnisse vs. Anpassungsergebnisse 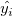
Residuen vs. die Ordnung der Datendiagramme
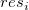 vs. Abfolgenummer vs. Abfolgenummer 
Histogramm des Residuums
Histogramm des Residuums
Verzögertes Residuendiagramm
Residuen 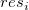 vs. verzögertes Residuum vs. verzögertes Residuum 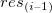
Wahrscheinlichkeitsnetz (Normal) für Residuen
Das Wahrscheinlichkeitsnetz der Residuen (Normal) kann verwendet werden, um zu prüfen, ob die Varianz ebenfalls normalverteilt ist. Wenn das sich ergebende Diagramm ungefähr linear ist, nehmen wir weiterhin an, dass die Fehlerterme normal verteilt sind. Das Diagramm basiert auf Perzentilen versus geordnete Residuen. Die Perzentile werden geschätzt mit
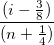
wobei n die Gesamtanzahl der Datensätze und i die i-ten Daten sind. Bitte lesen Sie auch Wahrscheinlichkeitsdiagramm und Q-Q-Diagramm.
|