アルゴリズム (線形多重回帰)Multi-Regression-Algorithm
線形多重回帰(重回帰)モデル
線形多重回帰(重回帰)モデル
線形多重回帰(重回帰)モデルは、単回帰モデルを拡張したもので、複数の独立変数が存在する場合に使用されます。これは、複数の独立変数 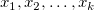 が従属変数yに及ぼす影響を解析するために用いられます。与えられたデータセット が従属変数yに及ぼす影響を解析するために用いられます。与えられたデータセット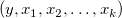 に対して、線形多重回帰は以下のモデルにフィットさせます: に対して、線形多重回帰は以下のモデルにフィットさせます:
ここで、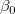 はy切片で はy切片で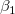 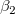 ,...はパラメータです。 ,...はパラメータです。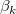 は部分回帰係数と呼ばれます。
次のように行列形式で書くこともできます。 は部分回帰係数と呼ばれます。
次のように行列形式で書くこともできます。
ここで
ここで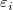 は、 は、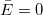 かつ かつ![Var[E]=\sigma^2 Var[E]=\sigma^2](//d2mvzyuse3lwjc.cloudfront.net/doc/ja/UserGuide/images/Multiple_Regression_Results/math-5d3cf3883ed3c4d0b917f9fc2e8f776b.png) の正規分布に従う独立同分布と仮定します。 の正規分布に従う独立同分布と仮定します。
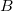 に関して に関して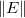 を最小化するために、次の関数を解きます。 を最小化するために、次の関数を解きます。
結果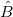 はベクトルBの最小二乗推定値であり、次の線形方程式を解いたものです。 はベクトルBの最小二乗推定値であり、次の線形方程式を解いたものです。
ここで、X'はXの転置行列です。
与えられたXに対するYの予測値は次のようになります。
式(4)の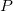 を代入することで行列 を代入することで行列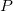 を定義することができます。 を定義することができます。
残差は次のように定義されます。
そして残差平方和は次のように表されます。
フィット制御
誤差を重みとする
フィット時に各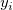 に重みを与えることができます。yEr±誤差列 に重みを与えることができます。yEr±誤差列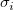 がある場合、この列は各 がある場合、この列は各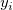 に対する重み に対する重み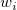 として扱われます。もしyEr±列が存在しない場合、すべての として扱われます。もしyEr±列が存在しない場合、すべての で で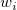 は 1 と見なされます。 は 1 と見なされます。
重み付きフィットにおける解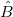 は、次のように表されます。 は、次のように表されます。
ここで
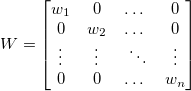
重み付けなし
エラーバーは計算において重みとして扱われません。
直接重み付け
機械的
切片固定
切片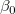 を固定値に設定すると、その分の自由度が減少し、自由度n*=n-1になります。 を固定値に設定すると、その分の自由度が減少し、自由度n*=n-1になります。
二乗値(自由度あたりカイ二乗値)でのスケールエラー
重み付きでフィッティングする場合、二乗値(自由度あたりカイ二乗値)でのスケールエラーが利用できます。このチェックボックスはパラメータの誤差推定値にのみ影響し、フィット計算やデータ自体には影響を与えません。
デフォルトでオンになっており、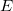 の分散 の分散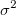 を考慮してパラメータ誤差が計算されます。オフにすると、 を考慮してパラメータ誤差が計算されます。オフにすると、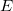 は考慮されません。
共分散行列を例にとると、 は考慮されません。
共分散行列を例にとると、
二乗値(自由度あたりカイ二乗値)でのスケールエラー
二乗値(自由度あたりカイ二乗値)でのスケールエラーでない
重み付けフィットでは、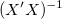 の代わりに の代わりに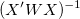 が使用されます。 が使用されます。
フィット結果
フィットパラメータ

フィット値
式 (4)
パラメータの標準誤差
各パラメータにおいて、標準誤差は以下のように得られます。
ここで、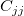 は は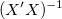 のj番目の対角要素です(重み付きフィットでは のj番目の対角要素です(重み付きフィットでは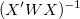 を使用します)。残差の標準偏差 を使用します)。残差の標準偏差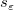 (“標準誤差”や “推定の標準誤差”、“MSEの平方根”とも呼ばれます)は以下で求めます。 (“標準誤差”や “推定の標準誤差”、“MSEの平方根”とも呼ばれます)は以下で求めます。
この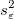 は、 は、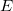 の分散 の分散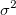 の推定値です。 の推定値です。
| Note:自由度(df)の詳細については、ANOVA表のdfErrorを参照してください。
|
t値と信頼水準
回帰の前提が成り立つと仮定すれば、回帰係数に対して以下の帰無仮説と対立仮説に基づく t検定 を行うことができます。
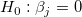
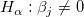
t値は次式で求められます。
計算されたt値を使って、対応する帰無仮説を棄却するかどうかを決定できます。通常与えられた有意水準 に対して、 に対して、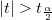 のときに のときに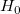 を棄却します。さらに、p値は を棄却します。さらに、p値は より小さくなります。 より小さくなります。
Prob>|t|
この値は、t検定における帰無仮説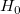 が正しい確率(p値)を示します。 が正しい確率(p値)を示します。
ここで、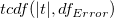 は、値|t|におけるスチューデントt分布の累積分布関数を、誤差の自由度 は、値|t|におけるスチューデントt分布の累積分布関数を、誤差の自由度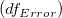 で計算します。 で計算します。
LCLおよびUCL
t値から各パラメータの信頼区間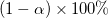 を次の式で計算できます。 を次の式で計算できます。
ここで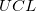 と と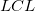 はそれぞれ上限信頼区間と下限信頼区間の略です。 はそれぞれ上限信頼区間と下限信頼区間の略です。
CI半幅
信頼区間の半幅は以下の通りです。
VIF
分散拡大係数は以下のように計算されます。
ここで、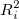 はi番目の独立変数を他のすべての独立変数で回帰した際の決定係数(補正なし)です。 はi番目の独立変数を他のすべての独立変数で回帰した際の決定係数(補正なし)です。
フィット統計
以下に、主要なフィット統計の数式をまとめます。

自由度
誤差変動の自由度。詳細はANOVA表を参照してください。
自由度あたりカイ二乗
残差平方和
残差平方和については、式 (8) を参照してください。
R二乗(COD)
フィットの良さ(適合度)は、決定係数(COD) 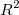 によって評価できます。以下の式で定義されます。 によって評価できます。以下の式で定義されます。
補正R二乗
補正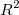 は自由度を考慮して は自由度を考慮して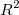 を調整した指標です。以下の式で求められます。 を調整した指標です。以下の式で求められます。
R値
R値は単純に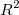 の平方根です。 の平方根です。
Root-MSE(SD)
Root-MSE(残差標準偏差)は以下の式で求められます
残差ノルム
残差平方和の平方根です。
ANOVA表
線形フィットのANOVA表は次のとおりです。
|
|
df
|
平方和
|
平均平方
|
F値
|
Prob > F
|
| モデル
|
k
|
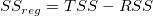
|
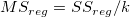
|
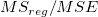
|
P値
|
| 誤差
|
n* - k
|
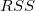
|
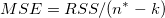
|
|
|
| 合計
|
n*
|
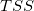
|
|
|
|
| Note:モデルに切片(定数項)を含む場合、自由度n*=n-1。含まない場合は、n *= nであり、で、TSS(全体平方和)は「補正なし」のものになります。
|
ここで、総平方和(TSS)は次のようになります。
ここでのF値は、フィッティングモデルが定数モデル(y = 定数)と有意に異なるかどうかを検定するための指標です。
また、p値または有意水準がF検定とともに出力されます。p 値があらかじめ設定された有意水準 未満であれば、帰無仮説(y = 定数)を棄却し、フィットモデルが有意であると判断できます。 未満であれば、帰無仮説(y = 定数)を棄却し、フィットモデルが有意であると判断できます。
切片を固定した場合(たとえば0に固定など)、F検定による p 値は有意な意味を持たず、切片を自由にフィットする通常の重回帰とは異なる解釈となります。
適合度検定表
適合度検定を実行するには、同じX値に対して複数の観測が存在する 繰り返しデータ(replicate data) が必要です。つまり、データセット内、または「連結フィット」モードを選択している場合は複数のデータセットにおいて、少なくとも1つのX値が繰り返されている必要があります。
複製データでフィットに使われている表記:
平方和は、次の通りです。
線形フィッティングの適合度検定表:
|
|
DF
|
平方和
|
平均平方
|
F値
|
Prob > F
|
| 不適合度
|
c-k-1
|
LFSS
|
MSLF = LFSS / (c - k - 1)
|
MSLF / MSPE
|
p値
|
| 純誤差
|
n - c
|
PESS
|
MSPE = PESS / (n - c)
|
|
|
| 誤差
|
n*-k
|
RSS
|
|
|
|
Note:
モデルに切片が含まれている場合、n *= n-1です。それ以外の場合は、n *= nで全体平方和は補正されません。傾きが固定されている場合、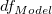 = 0になります。 = 0になります。
cはXの異なる値の個数(水準数)を表します。切片を固定している場合、不適合度の自由度はc-kとなります。
|
共分散行列と相関行列
線形多重回帰(重回帰)の共分散行列は、次のように計算できます。
任意の2つのパラメータ間の相関係数(ピアソンの相関)は次の式で求められます。
残差解析
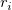 は通常の残差 は通常の残差 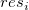 。 。
標準化
スチューデント化
内部スチューデント化残差とも呼ばれます。
スチューデント化削除
外部スチューデント化残差とも呼ばれる。
スチューデント化、スチューデント化削除での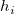 は、行列 は、行列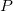 の i 番目の対角成分です。 の i 番目の対角成分です。
また、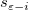 はi 番目のデータ点を除いて算出された誤差の分散です。 はi 番目のデータ点を除いて算出された誤差の分散です。
プロット
部分レバレッジプロット
線形多重回帰(重回帰)において、部分レバレッジプロットは、ある独立変数と従属変数との関係を検討するために使用されます。このプロットでは、Yの部分残差を Xまたは切片の部分残差に対してプロットします。ここでの「部分残差」とは、その変数をモデルから除いた状態での回帰残差です。
たとえば、モデル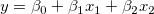 を考えます。このとき を考えます。このとき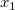 に対する部分レバレッジプロットは、 に対する部分レバレッジプロットは、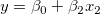 の残差回帰を の残差回帰を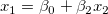 の残差に対してプロットすることで作成されます。 の残差に対してプロットすることで作成されます。
残差タイプ
作図には、標準、標準化、スチューデント化、スチューデント化残差から1つの残差タイプを選択します。
残差vs.独立
残差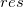 vs. 独立変数 vs. 独立変数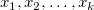 の散布図プロットではそれぞれのプロットは別々のグラフに配置されます。 の散布図プロットではそれぞれのプロットは別々のグラフに配置されます。
残差vs.予測値
残差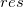 の散布図プロット vs. フィット結果 の散布図プロット vs. フィット結果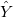
残差vs.データ順序
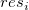 vs. 順序 vs. 順序
残差のヒストグラム
残差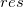 のヒストグラムプロット のヒストグラムプロット
残差のラグプロット
残差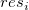 vs. ラグ残差 vs. ラグ残差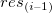
残差の正規確率プロット
残差の正規確率プロットは分散が成否分布しているかどうかを調べるために使います。結果のプロットはおおよそ線形で、誤差範囲は正規分布していると仮定することができます。このプロットは、順序付けられた残差に対するパーセンタイル値に基づいて作成され、パーセンタイルは以下の式で推定されます。
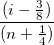
ここで、n はデータセットの合計数で、iはi番目のデータを表します。確率プロットとQ-Qプロットもご覧ください。
|