Algorithmus (Mehrfache Lineare Regression)
Multi-Regression-Algorithm
Das Modell der multiplen linearen Regression
Modell der multiplen linearen Regression
Die mehrfache lineare Regression ist eine Erweiterung der einfachen linearen Regression, bei der mehrere unabhängige Variablen existieren. Sie wird zum Analysieren der Auswirkung von mehr als einer unabhängigen Variablen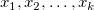 auf die abhängige Variable y verwendet. Für einen gegebenen Datensatz auf die abhängige Variable y verwendet. Für einen gegebenen Datensatz 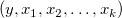 passt die mehrfache lineare Regression den Datensatz an das folgende Modell an: passt die mehrfache lineare Regression den Datensatz an das folgende Modell an:
wobei 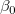 der Y-Achsenabschnitt ist und die Parameter der Y-Achsenabschnitt ist und die Parameter 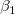 , , 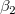 ,…, ,…, 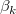 die teilweisen Koeffizienten genannt werden. Dies kann in Matrixform geschrieben werden: die teilweisen Koeffizienten genannt werden. Dies kann in Matrixform geschrieben werden:
wobei
Angenommen, 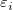 sind unabhängige und identisch verteilt wie normalverteilte Zufallsvariablen mit sind unabhängige und identisch verteilt wie normalverteilte Zufallsvariablen mit 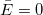 und und ![Var[E]=\sigma^2 Var[E]=\sigma^2](//d2mvzyuse3lwjc.cloudfront.net/doc/de/UserGuide/images/Multiple_Regression_Results/math-5d3cf3883ed3c4d0b917f9fc2e8f776b.png) . Um . Um 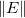 hinsichtlich hinsichtlich 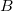 zu minimieren, lösen wir die Funktion: zu minimieren, lösen wir die Funktion:
Das Ergebnis 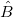 ist die Schätzung der kleinsten Quadrate des Vektors B. Es ist die Lösung der linearen Gleichungen, die folgendermaßen ausgedrückt werden können: ist die Schätzung der kleinsten Quadrate des Vektors B. Es ist die Lösung der linearen Gleichungen, die folgendermaßen ausgedrückt werden können:
wobei X’ die Transponierte von X ist. Der prognostizierte Wert von Y für einen gegebenen Wert von X ist:
Indem 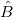 mit (4) ersetzt wird, wird die Matrix mit (4) ersetzt wird, wird die Matrix  definiert. definiert.
Die Residuen werden definiert als:
und die Residuensumme der Quadrate kann geschrieben werden als:
Fit-Steuerung
Fehler als Gewichtung
Wir können jeder 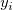 im Anpassungsprozess eine Gewichtung geben. Die Fehlerspalte yEr± im Anpassungsprozess eine Gewichtung geben. Die Fehlerspalte yEr± 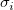 wird als Gewichtung wird als Gewichtung 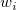 für jeden für jeden 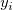 behandelt, wenn yEr± nicht vorhanden ist. behandelt, wenn yEr± nicht vorhanden ist. 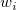 sollte für alle sollte für alle  1 sein. 1 sein.
Die Lösung 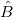 für die Anpassung mit Gewichtung kann geschrieben werden als: für die Anpassung mit Gewichtung kann geschrieben werden als:
wobei
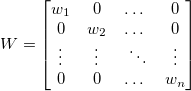
Keine Gewichtung
Der Fehlerbalken wird in der Berechnung nicht als Gewichtung behandelt.
Direkte Gewichtung
Instrumentell
Fester Schnittpunkt mit der Y-Achse (bei)
Fester Schnittpunkt mit der Y-Achse legt den Y-Schnittpunkt 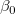 auf einen festen Wert fest, während der Gesamtfreiheitsgrad n*=n-1 ist aufgrund des festgelegten Schnittpunkts mit der Y-Achse. auf einen festen Wert fest, während der Gesamtfreiheitsgrad n*=n-1 ist aufgrund des festgelegten Schnittpunkts mit der Y-Achse.
Skalierungsfehler mit Quadrat (Reduziertes Chi-Quadrat)
Die Option Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) ist verfügbar, wenn mit Gewichtung angepasst wird. Diese Option beeinflusst nur den Fehler auf die Parameter, die der Anpassungsprozess meldet, und nicht den Anpassungsprozess selbst oder die Daten in irgendeiner Weise. Die Option ist standardmäßig aktiviert, und 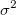 , die Varianz von , die Varianz von 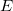 , wird zum Berechnen der Fehler auf die Parameter berücksichtigt. Ansonsten wird die Varianz von , wird zum Berechnen der Fehler auf die Parameter berücksichtigt. Ansonsten wird die Varianz von 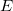 nicht zur Fehlerberechnung berücksichtigt. Die Kovarianzmatrix soll als Beispiel dienen: nicht zur Fehlerberechnung berücksichtigt. Die Kovarianzmatrix soll als Beispiel dienen:
Skalierungsfehler mit Quadrat (Reduziertes Chi-Quadrat)
Keinen Skalierungsfehler mit Quadrat (Reduziertes Chi-Qdr.) verwenden:
Für die gewichtete Anpassung wird 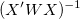 anstatt anstatt 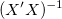 verwendet. verwendet.
Fit-Ergebnisse
Fit-Parameter

Die angepassten Werte
Formel (4)
Die Parameterstandardfehler
Für jeden Parameter kann der Standardfehler, wie folgt, ermittelt werden:
wobei 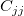 das j-te diagonale Element von das j-te diagonale Element von 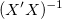 ist (beachten Sie, dass ist (beachten Sie, dass 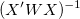 für die gewichtete Anpassung verwendet wird). Die Standardabweichung der Residuen für die gewichtete Anpassung verwendet wird). Die Standardabweichung der Residuen 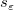 (auch “StdAbw”, “Standardfehler der Schätzung” oder “Wurzel-MSE”) wird berechnet mit: (auch “StdAbw”, “Standardfehler der Schätzung” oder “Wurzel-MSE”) wird berechnet mit:
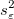 ist eine Schätzung von ist eine Schätzung von 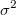 . Dies ist die Varianz von . Dies ist die Varianz von 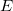 . .
| Hinweis: Bitte lesen Sie weitere Einzelheiten zu den Freiheitsgraden, dfError, unter ANOVA-Tabelle. |
t-Wert und Konfidenzniveau
Bleiben die die Regressionsannahmen bestehen, können wir die t-Tests für die Regressionskoeffizienten mit der Nullhypothese und der Alternativhypothese ausführen:
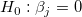
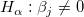
Die t-Werte können wie folgt berechnet werden:
Mit dem berechneten t-Wert können wir entscheiden, ob die entsprechende Nullhypothese verworfen werden soll oder nicht. Gewöhnlich können wir für ein gegebenes Konfidenzniveau für Parameter:  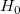 verwerfen, wenn verwerfen, wenn 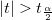 . Zusätzlich ist der p-Wert kleiner als . Zusätzlich ist der p-Wert kleiner als  . .
Wahrsch.>|t|
Die Wahrscheinlichkeit, dass 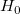 in dem t-Test oben wahr ist. in dem t-Test oben wahr ist.
wobei 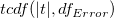 die kumulative Verteilungsfunktion der studentischen t-Verteilung bei den Werten |t| berechnen mit dem Freiheitsgrad des Fehlers die kumulative Verteilungsfunktion der studentischen t-Verteilung bei den Werten |t| berechnen mit dem Freiheitsgrad des Fehlers 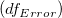 . .
UEG und OEG
Mit dem t-Wert können wir das 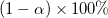 -Konfidenzintervall für jeden Parameter berechnen: -Konfidenzintervall für jeden Parameter berechnen:
wobei 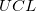 und und 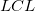 für Oberes Konfidenzintervall bzw. Unteres Konfidenzintervall steht. für Oberes Konfidenzintervall bzw. Unteres Konfidenzintervall steht.
KI halbe Breite
Das Konfidenzintervall halbe Breite ist:
VIF
Der Varianzinflationsfaktor ist:
Wobei: 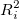 ist ein nicht korrigierter Determinationskoeffizient für die Regression der i-ten unabhängigen Variable auf die verbleibenden. ist ein nicht korrigierter Determinationskoeffizient für die Regression der i-ten unabhängigen Variable auf die verbleibenden.
Anpassungsstatistik
Einige Fit-Statistikformeln werden hier zusammengefasst:
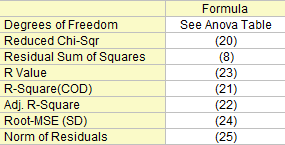
Freiheitsgrade
Der Freiheitsgrad für (Fehler) Streuung Weitere Einzelheiten finden Sie in der ANOVA-Tabelle.
Reduziertes Chi-Quadrat
Summe der Fehlerquadrate
Die Residuensumme der Quadrate, siehe Formel (8).
R-Quadrat (COD)
Die Anpassungsgüte kann durch den Determinationskoeffizienten (COD) 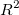 bewertet werden, der gegeben ist mit: bewertet werden, der gegeben ist mit:
Kor. R-Quadrat
Der korrigierte 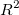 wird zum Anpassen des wird zum Anpassen des 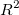 -Wertes für den Freiheitsgrad verwendet. Es kann wie folgt berechnet werden: -Wertes für den Freiheitsgrad verwendet. Es kann wie folgt berechnet werden:
R-Wert
Anschließend können wir den R-Wert berechnen, der einfach die Quadratwurzel von 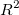 ist: ist:
Wurzel-MSE (StAbw)
Quadratwurzel des Mittelwerts des Fehlers oder die residuale Standardabweichung ist gleich:
Betrag der Residuen
Ist gleich der Quadratwurzel von RSS:
ANOVA-Tabelle
Die ANOVA-Tabelle der linearen Anpassung ist:
|
Freiheitsgrade |
Summe der Quadrate |
Mittelwert der Quadrate |
F -Wert |
Wahrsch. > F |
| Modell |
k |
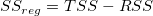 |
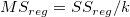 |
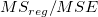 |
p-Wert |
| Fehler |
n* - k |
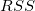 |
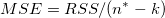 |
|
|
| Gesamt |
n* |
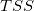 |
|
|
|
| Hinweis: Wenn der Schnittpunkt mit der Y-Achse im Modell enthalten ist, dann ist n*=n-1. Andernfalls ist n*=n und die Gesamtsumme der Quadrate ist unkorrigiert. |
Dabei ist hier die Gesamtsumme der Quadrate, TSS:
Der F-Wert ist ein Test, ob das Anpassungsmodell sich signifikant von dem Modell Y = konstant unterscheidet.
Zusätzlich werden der p-Wert bzw. die Signifikanzebene mit einem F-Test ermittelt. Wir können die Nullhypothese verwerfen, wenn der p-Wert kleiner als  ist, das heißt, das Anpassungsmodell unterscheidet sich signifikant von dem Modell Y = konstant. ist, das heißt, das Anpassungsmodell unterscheidet sich signifikant von dem Modell Y = konstant.
Wenn der Schnittpunkt mit der Y-Achse bei einem bestimmten Wert festgelegt wird, ist der p-Wert für den F-Test nicht bedeutungsvoll und unterscheidet sich von dem in der multiplen linearen Regression ohne die Nebenbedingung des Schnittpunkts mit der Y-Achse.
Tabelle des Tests auf fehlende Anpassung
Um den Test auf fehlende Anpassung auszuführen, müssen Sie sich wiederholende Beobachtungen zur Verfügung haben, d. h. "replizierte Daten" , so dass mindestens einer der X-Werte sich innerhalb des Datensatzes oder innerhalb mehrerer Datensätze wiederholt, wenn der Modus Zusammengefasster Fit ausgewählt ist.
Die Summe der Quadrate in der Tabelle unten wird ausgedrückt mit:
Die Tabelle des Tests auf fehlende Anpassung der linearen Anpassung ist:
|
Freiheitsgrade |
Summe der Quadrate |
Mittelwert der Quadrate |
F -Wert |
Wahrsch. > F |
| Fehlende Anpassung |
c-k-1 |
LFSS |
MSLF = LFSS / (c - k - 1) |
MSLF / MSPE |
p-Wert |
| Reiner Fehler |
n - c |
PESS |
MSPE = PESS / (n - c) |
|
|
| Fehler |
n*-k |
RSS |
|
|
|
Hinweis:
Wenn der Schnittpunkt mit der Y-Achse im Modell enthalten ist, dann ist n*=n-1. Andernfalls ist n*=n und die Gesamtsumme der Quadrate ist unkorrigiert. Wenn die Steigung fest ist, ist 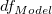 = 0. = 0.
c bezeichnet die Anzahl der eindeutigen X-Werte. Wenn der Schnittpunkt mit der Y-Achse festgelegt ist, ist der Freiheitsgrad für die fehlende Anpassung c-k.
|
Kovarianz- und Korrelationsmatrix
Die Kovarianzmatrix für die multiple lineare Regression kann, wie folgt, berechnet werden:
Die Korrelation zwischen zwei beliebigen Parametern ist:
Residuenanalyse
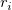 steht für reguläres Residuum steht für reguläres Residuum 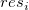 . .
Standardisiert
Studentisiert
Sind auch bekannt als intern studentisierte Residuen.
Studentisiert gelöscht
Sind auch bekannt als extern studentisierte Residuen.
In den Gleichungen der studentisierten und studentisiert gelöschten Residuen ist 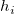 das i-te diagonale Element der Matrix das i-te diagonale Element der Matrix  : :
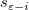 bedeutet die Varianz wird berechnet, basierend auf alle Punkte, schließt aber den iten Punkt aus. bedeutet die Varianz wird berechnet, basierend auf alle Punkte, schließt aber den iten Punkt aus.
Diagramme
Partielle Hebelwirkungsdiagramme
Bei der mehrfachen Regression können partielle Hebelwirkungsdiagramme verwendet werden, um das Verhältnis zwischen den unabhängigen und einer gegebenen abhängigen Variablen zu untersuchen. In dem Diagramm wird das partielle Residuum von Y gegen das partielle Residuum von X oder den Schnittpunkt mit der Y-Achse gezeichnet. Das partielle Residuum einer bestimmten Variablen ist das Regressionsresiduum, wobei diese Variable in dem Modell ausgelassen ist.
Nimmt man das Modell 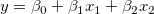 als Beispiel: Das partielle Hebelwirkungsdiagramm für als Beispiel: Das partielle Hebelwirkungsdiagramm für 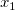 wird erstellt, indem das Regressionsresiduum von wird erstellt, indem das Regressionsresiduum von 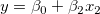 gegen das Residuum von gegen das Residuum von 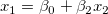 gezeichnet wird. gezeichnet wird.
Residuentyp
Wählen Sie einen Residuentyp unter Regulär, Standardisiert, Studentisiert, Studentisiert gelöscht für die Diagramme.
Residuen vs. Unabhängige
Punktdiagramm der Residuen 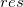 vs. unabhängige Variable vs. unabhängige Variable 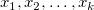 ; jede Zeichnung befindet sich in einem separaten Diagramm. ; jede Zeichnung befindet sich in einem separaten Diagramm.
Residuen vs. prognostizierte Werte
Punktdiagramm der Residuen 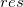 vs. Fit-Ergebnisse vs. Fit-Ergebnisse 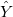 . .
Residuen vs. die Ordnung der Daten
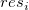 vs. Abfolgenummer vs. Abfolgenummer 
Histogramm des Residuums
Histogramm des Residuums 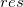
Verzögertes Residuendiagramm
Residuen 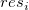 vs. zeitverzögertes Residuum vs. zeitverzögertes Residuum 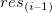 . .
Wahrscheinlichkeitsnetz (Normal) für Residuen
Das Wahrscheinlichkeitsnetz der Residuen (Normal) kann verwendet werden, um zu prüfen, ob die Varianz ebenfalls normalverteilt ist. Wenn das sich ergebende Diagramm ungefähr linear ist, nehmen wir weiterhin an, dass die Fehlerterme normal verteilt sind. Das Diagramm basiert auf Perzentilen versus geordnete Residuen. Die Perzentile werden geschätzt mit
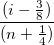
wobei n die Gesamtanzahl der Datensätze ist und i die i-ten Daten bezeichnet. Bitte lesen Sie auch Wahrscheinlichkeitsdiagramm und Q-Q-Diagramm.
|