xyz_tps
概要
Thin Plane スプライン補間
コマンドラインでの使用法
1. xyz_tps iz:=Col(3);
2. xyz_renka iz:=Col(3) rows:=20 cols:=20;
3. xyz_tps iz:=Col(3) s:=0.8;
4. xyz_renka iz:=Col(3) om:=[MBook]MSheet!Mat(1);
変数
表示
名 |
変数
名 |
I/O
と
データ型 |
デフォルト
値 |
説明 |
| 入力 |
iz |
入力
XYZRange
|
|
入力XYZ範囲の指定
|
| 行 |
rows |
入力
int
|
35
|
出力行列の行
|
| 列 |
cols |
入力
int
|
35
|
出力行列の列
|
| スムージング |
s |
入力
double
|
0.5
|
これは入力データポイントを超えるグリッド表面の広がりを指定する非負の値です。因数がゼロの場合、スムージング処理は行われず、補間面は全てのデータポイントを通過します。正の因数は表面スムーザを生成しますが、余り大きな因数にすると元データの全ての情報を保持することができなくなります。
|
| 外れ値 |
outlier |
入力
int
|
extrap
|
入力データが不規則で補間によって行列を完全に埋めることができない場合、外れ値にあたる箇所に指定した値を配置します。(下記参照)
オプションリスト
- extrap:補外
- TPSアルゴリズムに基づく外挿点を外れ値に割り当てます。 (デフォルトの設定)
- missing:欠損値
- 外れ値を欠損値とします。
- zero:ゼロ
- 外れ値をゼロとします。
- min:最小
- Z列の最小値を外れ値に割り当てます。
- Max:最大
- Z列の最大値を外れ値に割り当てます。
- mean:平均
- Z列の平均値を外れ値に割り当てます。
- custom:カスタム値
- 指定したカスタム値を外れ値に割り当てます。
|
| 外部 |
outside_val |
入力
double
|
100
|
結果行列内の外れ値に割り当てるカスタム値を指定します。外れ値フィールドの カスタム値オプションが選択されている場合にのみカスタム値を指定できます。
|
| 許容値 |
tolerance |
入力
double
|
5E-3
|
入力データの周囲が矩形かどうか決定する際の許容値を指定します。この変数は外れ値フィールドに外挿が選択されている場合には選択することができません。
|
| 出力行列 |
om |
出力
MatrixObject
|
<新規>
|
ここでは、行列ワークシート名を含む出力結果の宛先や形式などを指定します。
|
| 正則化 |
r |
出力
double
|
<unassigned>
|
正則化変数、ここでは曲げエネルギーの 加重として機能します。このパラメータはスムージング因数に比例し、スムージング因数がゼロでない場合にのみ有効となります。これは、入力されたスムージング因数に基づいて計算されたパラメータです。
|
説明
この関数はTPS(Thin Plate Spline)アルゴリズムに基づいたランダムな行列変換を行う手法を提供します。これは、XYZグリッディングダイアログボックスにも表示されます。
TPSは物理的な補間手法です。グリッディングデータを生成するために、この手法では、全てのデータポイントは薄い、伸縮性のある平面や平板に分配されると仮定します。平面 はグリッドポイントを移動しないよう制約されます。スプラインはグリッドポイントを補間することによって2次元の曲面を形成します。曲面はデータに対して適当なフィットを行うために、データ間で変形されます。最善の結果は、通常、いわゆる平面の"曲げエネルギー関数"を最小化することよって得ることができます。
TPSは局所的な水平面の2次元補間に適した手法です。
サンプル
1. ファイル\Samples\Matrix Conversion and Gridding\ XYZ Random Gaussian.datをインポートします。
2. 次のコマンドを入力し、Enterキーを押します。
xyz_tps iz:=Col(3) rows:=50 cols:=50
行列がイメージモードで新しいウィンドウ内でグラフ化されます。
他のサンプルについては、XFスクリプトダイアログ(F11を押す)をご覧下さい。
アルゴリズム
Thin Plate Spline (TPS) アルゴリズムは散布データのための補間法です。TPS プロセスは薄い、伸縮性のある、平面 (または曲面)をグリッド点に固定し、全てのデータポイントを通過するように曲面を持ち上げるのに似た作業です。 TPS のアルゴリズムによって、全てのデータポイントと最小のいわゆる曲げエネルギー関数の両方を取得する関数を構築します。
曲げエネルギー関数は次のように定義されます。
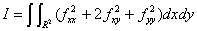 . .
数式の最小化関数です。
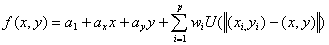 , ,
ここで 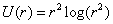 , と , と 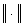 はベクトルの大きさを示しています。 はベクトルの大きさを示しています。
規則化パラメータは曲げエネルギーの重み付けとして機能します。ゼロに近い規則化パラメータは全てのデータポイントに接近しますが、ノイズの多いデータの場合、粗い曲面を作成してしまいます。大きな規則化パラメータはデータをより滑らかにしますが、個々のデータへのフィットの厳密さは失われてしまいます。そのため、規則化パラメータは補間の必要条件の厳密さを示すものとなります。このパラメータは入力されたスムージング因数に基づいて計算されます。
XYZ のデータポイントを xi, yi, zi, で表す場合、i = 1, 2, ... N, となります。
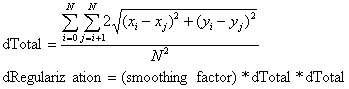
最小の曲げエネルギーを検出するためには、より算術的な変換が必要とされます。アルゴリズムの詳細に興味のあるユーザは以下の参考文献をご一読ください。
参考文献
[1].Bookstein, F.L."Principal Warps: Thin Plate Splines and the Decomposition of Deformations." IEEE Trans.Pattern Anal.Mach.Intell.11, 567-585 (1989)
[2].Craven, P.and Wahba, G."Smoothing Noisy Data with spline Functions".Numer.Math 31, 377-403 (1979).
[3].Donato, Gianluca and Serge Belongie, "Approximation Methods for Thin Plate spline Mappings and Principal Warps" 2002.
関連のXファンクション
xyz_regular, xyz_renka, xyz_renka_nag, xyz_shep, xyz_shep_nag, xyz_sparse
|