xyz_shep
概要
修正シェパードグリッディング法
コマンドラインでの使用法
1. xyz_shep iz:=Col(3);
2. xyz_renka iz:=Col(3) rows:=10 cols:=10;
4. xyz_shep iz:=Col(3) q:=13 w:=19;
5. xyz_renka iz:=Col(3) om:=[MBook]MSheet!Mat(1);
変数
表示
名 |
変数
名 |
I/O
と
データ型 |
デフォルト
値 |
説明 |
| 入力 |
iz |
入力
XYZRange
|
<active>
|
入力XYZ範囲の指定
|
| 行 |
rows |
入力
int
|
20
|
出力行列の行
|
| 列 |
cols |
入力
int
|
20
|
出力行列の列
|
| 二次因子 |
q |
入力
int
|
13
|
二次間局所因数は各ノードに対して局所近似二次フィット関数が影響を及ぼす範囲を計算するのに利用されます。デフォルトで q は 13に等しくなります。これらの因数を変更することにより グリッディングの精度を上げることができますが、計算時間は非常に大きな値(言い換えれば、手法の局所性を減少させる値) になります。
|
| 重み付け |
w |
入力
int
|
19
|
加重関数局所因数は各ノードの重み付け半径を算出するのに利用されます。デフォルトでは、wは19に等しくなっています。これらの因数を変更することにより グリッディングの精度を上げることができますが、計算時間は非常に大きな値(言い換えれば、手法の局所性を減少させる値) になります。
|
| 出力行列 |
om |
出力
MatrixObject
|
<新規>
|
出力行列オブジェクトの指定
|
説明
この関数はRenkaによって記述された修正シェパードグリッディング法を実行します。[1].これは距離ベースの手法であり、いくつかの局所的方法によってシェパード法を改良したものです。グリッディングの間、ある範囲内にあるデータ Rq および Rwのみをグリッドノードとして扱います。設定を簡単にするために、2つの整数 Nq および Nw を Rq と Rw を算出するのに使用します。(関数のパラメータである q と w そしてそれぞれ 二次間局所因数 と 加重関数局所因数と呼ばれます) Nq と Nwの値を増加させるとより広範囲の演算がなされます。逆もまた同様です。一般的に言って、 Nq=13 と Nw=19 という設定はかなり良い結果をもたらします。
この関数の Rq と Rw はノードごとに変動します。もう1つの似た働きを持つXファンクションでFranke と Nielson[2] によって記述された xyz_shep_nag では固定された Rq と Rw を計算に利用します。
サンプル
1. Samples\Matrix Conversion and Gridding フォルダから XYZ Random Gaussian.dat を インポートします。
2. xyz_renka 3 とコマンドウィンドウに入力します。または xyz_shep d と表示されるダイアログに入力します。
他のサンプルについては、XFスクリプトダイアログ(F11を押す)をご覧下さい。
アルゴリズム
これは以下のようにデータを取り込む距離ベースの加重グリッディング法です。
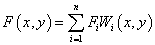 , ,
ここで Fi はノード (xi, yi) に内在する関数であり、 Wi(x, y) は加重となります。より局所的な関数を作成するには、 Fi と Wi は中央の (xi, yi) と半径 Rとの間にあるもののみで計算します。
初めに、加重を以下のように定義します。
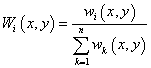 . .
与えられた半径 Rw、 相対的重さ wk は
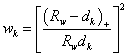 この場合、 この場合、
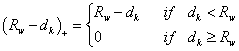 , ,
dk は (x, y) (xk, yk) との間のユークリッド距離です。
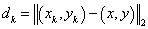 . .
Rw>0の場合、
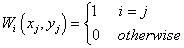
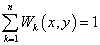 . .
次に, 節点関数 Fi は局所近似関数の Qk によって置き換えられます。
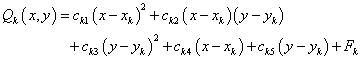
Qk は 結節点Rq 内に位置するデータ用の加重最小二乗二次近似関数です。係数を最小化するには
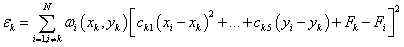
この場合、
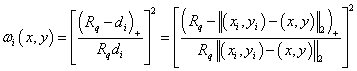 . .
上述のように、補間関数は局所近似関数であり、RqとRwという結節点周辺の影響圏に依存します。 この手法では、 Rq と Rw はより精密に演算を実行するために、結節点ごとに変化します。2つの整数 Nq と Nw が与えられ、Rq と Rw は Nq と Nw の節を含めるのに充分な大きさが選択されます。
参考文献
[1].Renka, R.J., Multivariate Interpolation of Large Sets of Scattered Data.ACM Transactions on Mathematical Software, Vol.14, No.2, June 1988, pp:139-148.
[2].Franke R and Nielson G.smooth Interpolation of Large Sets of Scattered Data.Internat.J.Num.Methods Engrg.1980, 15 pp:1691-1704.
関連のXファンクション
xyz_regular, xyz_renka, xyz_renka_nag, xyz_shep_nag, xyz_sparse, xyz_tps
|