2.2.1.8 xyz_shep
Brief Information
Convert XYZ data to matrix using Shepard gridding
Command Line Usage
1. xyz_shep iz:=Col(3);
2. xyz_shep iz:=Col(3) rows:=10 cols:=10;
3. xyz_shep iz:=Col(3) q:=13 w:=19;
4. xyz_shep iz:=Col(3) om:=[MBook]MSheet!Mat(1);
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
iz
|
Input
XYZRange
|
<active>
|
Specifies the input XYZ range.
|
| Rows
|
rows
|
Input
int
|
20
|
Rows in the output matrix.
|
| Columns
|
cols
|
Input
int
|
20
|
Columns in the output matrix.
|
| Quadratic
|
q
|
Input
int
|
13
|
The quadratic interplant locality factor, which is used to calculate the influence radius of local approximate quadratic fitted function for each node. By default, q equals to 13. Modifying these factors could increase gridding accuracy, though note that the computation time can be greatly increased for large values (i.e. values that decrease the locality of the method.)
|
| Weight
|
w
|
Input
int
|
19
|
The weight function locality factor, which is used to calculate the weighting radius for each node. By default, w equals to 19. Modifying these factors could increase gridding accuracy, though note that the computation time can be greatly increased for large values (i.e. values that decrease the locality of the method.)
|
| Output Matrix
|
om
|
Output
MatrixObject
|
<new>
|
Specify the output matrix object.
See the syntax here.
|
Description
This function performs modified Shepard gridding method which described by Renka[1]. This is a distance-based method and improves the Shepard's method by some local strategies. During gridding, only the data points that lying within certain ranges, 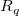 and and 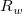 , to the grid nodes are considered. To make it easier for setting, two integers, , to the grid nodes are considered. To make it easier for setting, two integers, 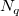 and and 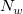 are used to calculate are used to calculate 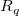 and and 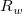 (parameters q and w of the function, and called Quadratic Interplant Locality Factor and Weight Function Locality Factor, respectively). Increase the value of (parameters q and w of the function, and called Quadratic Interplant Locality Factor and Weight Function Locality Factor, respectively). Increase the value of 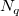 and and 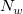 will make the calculation more global, vice versa. Generally speaking, setting will make the calculation more global, vice versa. Generally speaking, setting 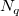 and and 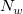 works quite well. works quite well.
The value of 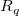 and and 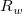 in this function is varied for each node. There is another similar X-Function xyz_shep_nag which described by Franke and Nielson[2] uses a fixed in this function is varied for each node. There is another similar X-Function xyz_shep_nag which described by Franke and Nielson[2] uses a fixed 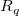 and and 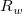 calculation. calculation.
Examples
- To run from Command window
- Import XYZ Random Gaussian.dat on the \Samples\Matrix Conversion and Gridding folder.
- Type
xyz_shep 3 in the command window. Or type xyz_shep -d to bring up the dialog.
/*
This example shows how convert random worksheet data into matrix by Shepard gridding method.
The sample data is exe_path\Samples\Matrix Conversion and Gridding\XYZ Random Gaussian.dat
1. Load data to a new created workbook.
2. Random xyz gridding by Shepard method.
3. Plot a contour graph.
*/
// Get sample data
fn$ = system.path.program$ + "Samples\Matrix Conversion and Gridding\XYZ Random Gaussian.dat";
newbook;
impASC fn$;
// Set the third column as Z column
wks.col3.type = 6;
// Convert worksheet data into matrix by Shepard gridding method
xyz_shep 3;
// Plot
worksheet -p 226 contour;
Algorithm
This is a distance-based weighted gridding method which interpolate data by:
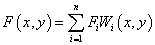 , ,
where 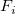 is the underlying function at nodes ( is the underlying function at nodes (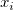 , , 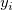 ), and ), and 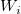 (x, y) is the weights. To make the function more local, (x, y) is the weights. To make the function more local, 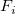 and and 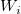 are calculated only by the data points lying in the circle with center ( are calculated only by the data points lying in the circle with center (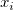 , , 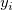 ) and some radius R.. ) and some radius R..
Firstly, the weights are defined as:
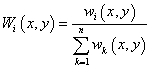 . .
Given a radius (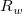 , the relative weight ( , the relative weight (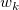 is: is:
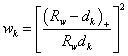 for for
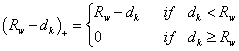 , ,
and (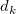 is the Euclidean distance between (x, y) and ( is the Euclidean distance between (x, y) and (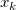 , , 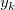 ): ):
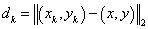 . .
For any (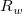 >0, we have: >0, we have:
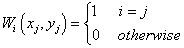
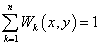 . .
Secondly, the nodal function (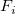 is replaced by a local approximation function is replaced by a local approximation function 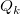 : :
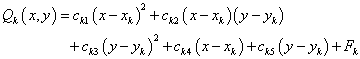
(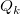 is the weighted least-square quadratic fitted function to the data located within ( is the weighted least-square quadratic fitted function to the data located within (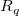 of nodal points. So the coefficients minimize: of nodal points. So the coefficients minimize:
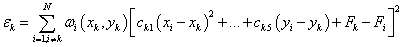
for
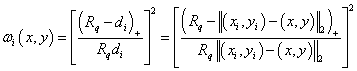 . .
It can be seen above that the interpolate function is a local approximation function and depends on the radius of influence about nodal points, (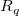 and ( and (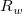 . In this method, ( . In this method, (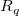 and ( and (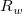 are varied for each nodal point to make the calculation more accurate. Given two integers ( are varied for each nodal point to make the calculation more accurate. Given two integers (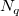 and ( and (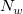 , ( , (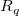 and ( and (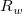 are chosen just large enough to include ( are chosen just large enough to include (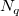 and ( and (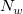 nodes. nodes.
References
[1]. Renka, R. J., Multivariate Interpolation of Large Sets of Scattered Data. ACM Transactions on Mathematical Software, Vol. 14, No. 2, June 1988, pp:139-148.
[2]. Franke R and Nielson G. smooth Interpolation of Large Sets of Scattered Data. Internat. J.Num. Methods Engrg. 1980, 15 pp:1691-1704.
Related X-Functions
xyz_regular, xyz_renka, xyz_renka_nag, xyz_shep_nag, xyz_sparse, xyz_tps
Keywords:worksheet
|