Dialog Zeilenstatistik
DescStatsRow-Dialog
Hilfreiche Informationen
Eingabe
Eigenschaften
Momente
- Angenommen
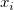 ist die i-te Stichprobe und ist die i-te Stichprobe und 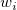 die i-te Gewichtung. die i-te Gewichtung.
| N gesamt |
Gesamtanzahl der Datenpunkte, bezeichnet mit n |
| N fehlend |
Anzahl der fehlenden Werte |
| Mittelwert |
Der (durchschnittliche) Mittelwert
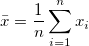 . .
|
| Standardabweichung |
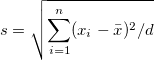
wobei 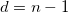
Hinweis: In OriginPro hat 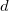 eine Option mehr, die im Zweig Varianzdivisor des Moments definiert ist. eine Option mehr, die im Zweig Varianzdivisor des Moments definiert ist.
|
| SE des Mittelwerts |
Standardfehler des Mittelwerts
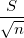
|
| Unteres 95% KI des Mittelwerts |
Untere Grenze des 95%-Konfidenzintervalls des Mittelwerts
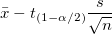
wobei 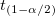 der der 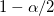 kritische Wert der Studenten-t-Statistik mit n-1 Freiheitsgraden ist. kritische Wert der Studenten-t-Statistik mit n-1 Freiheitsgraden ist.
|
| Oberes 95% KI des Mittelwerts |
Obere Grenze des 95%-Konfidenzintervalls des Mittelwerts
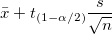
wobei 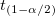 der der 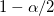 kritische Wert der Studenten-t-Statistik mit n-1 Freiheitsgraden ist. kritische Wert der Studenten-t-Statistik mit n-1 Freiheitsgraden ist.
|
| Varianz |
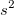 |
| Summe |
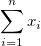 . . |
| Schiefe |
Die Schiefe misst den Grad der Asymmetrie einer Verteilung. Sie wird definiert als
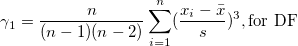
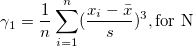
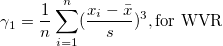
|
| Kurtosis |
Die Kurtosis zeigt den Grad der Peaks einer Verteilung an.
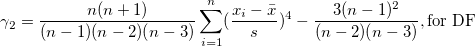
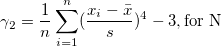
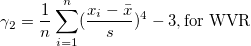
|
| Unkorrigierte Summe der Quadrate |
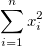
|
| Korrigierte Summe der Quadrate |
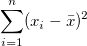
|
| Variationskoeffizient |
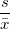
|
| Mittelwert Absolutabweichung |
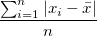
|
| SD mal 2 |
Standardabweichung mal 2
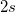
|
| SD mal 3 |
Standardabweichung mal 3
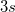
|
| Geometrische Mittelwert |
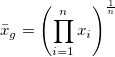
|
| Geometrische StAbw |
Die geometrische Standardabweichung 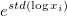 , wobei std für die ungewichtete Standardabweichung der Stichprobe steht. , wobei std für die ungewichtete Standardabweichung der Stichprobe steht.
Hinweis: Gewichtungen werden für die geometrische Standardabweichung ignoriert.
|
| Modus |
Der Modus ist das Element, das am häufigsten im Datenbereich auftaucht. Wenn mehrere Modi gefunden werden, wird das kleinste gewählt.
|
| Harmonisches Mittel |
Harmonisches Mittel
ohne Gewichtung: 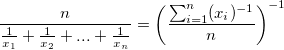
mit Gewichtung: 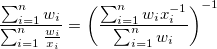
wenn 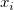 oder Gewichtung negativ ist, wird Fehlende weitergegeben; wenn oder Gewichtung negativ ist, wird Fehlende weitergegeben; wenn 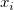 oder Gewichtung 0 ist, wird 0 weitergegeben. oder Gewichtung 0 ist, wird 0 weitergegeben.
|
Quantile
Quantile sind Werte aus Daten, unter denen sich ein gegebener Anteil der Datenpunkte in einem gegebenen Satz befindet. Zum Beispiel befinden sich 25% der Datenpunkte in einem beliebigen Datensatz unter dem ersten Quartil und 50% der Datenpunkte in einem Satz unter dem zweiten Quartil oder Median.
Sortieren Sie den Eingabedatensatz in aufsteigender Reihenfolge. Angenommen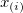 ist das i-te Element des neu geordneten Datensatzes. ist das i-te Element des neu geordneten Datensatzes.
| Minimum |
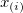 |
| Index des Minimums |
Die Indexnummer des Minimums im ursprünglichen (Eingabe-)Datensatz
|
| 1. Quartil (Q1) |
Erstes (25%) Quantil, Q1 Informationen zu Berechnungsmethoden finden Sie unter Interpolation von Quantilen. |
| Median |
Median oder zweites (50%) Quantil, Q2 Informationen zu Berechnungsmethoden finden Sie unter Interpolation von Quantilen. |
| 3. Quartil (Q3) |
Drittes (75%) Quantil, Q3 Informationen zu Berechnungsmethoden finden Sie unter Interpolation von Quantilen. |
| Maximum |
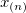 |
| Index des Maximums |
Die Indexnummer des Maximums im ursprünglichen (Eingabe-)Datensatz
|
| Interquartilbereich (Q3-Q1) |

|
| Spannweite (Maximum-Minimum) |
Maximum - Minimum
|
| Benutzerdefinierte Perzentil(e) |
Benutzerdefinierte Perzentile können berechnet werden.
|
| Perzentilliste |
Diese Option ist nur verfügbar, wenn Benutzerdefinierte Perzentil(e) aktiviert ist. Perzentile werden für alle aufgeführten Werte berechnet.
|
| Mittlere absolute Abweichung (MAD) |
Für einen univariaten Datensatz X1, X2, ..., Xn, wird MAD als Median der absoluten Abweichungen vom Median der Daten definiert:
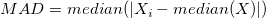
das heißt, angefangen bei den Residuen (Abweichungen) vom Median der Daten, ist die mittlere absolute Abweichung MAD der Median ihrer absoluten Werte.
|
| Robuster Variationskoeffizient |
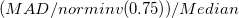
|
Steuerung Berechnung
Varianzdivisor des Moments
- Die Berechnung des Varianzdivisors d wird gesteuert.
| Freiheitsgrade |
Freiheitsgrade
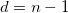
|
| N |
Anzahl der nicht fehlenden Beobachtungen

|
Interpolation der Quantile
- Mit dieser Option wird die Methode festgelegt, mit der Q1, Q2, and Q3 berechnet werden.
- Angenommen das i-te Perzentil ist y,
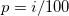 wird eingestellt und wird eingestellt und
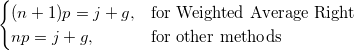
- wobei j der ganzzahlige Teil von np ist und g der Bruchteil von np. Verschiedene Methoden definieren das
 Perzentil y wie im Folgenden beschrieben: Perzentil y wie im Folgenden beschrieben:
Ausgabe
| Berichtstabellen |
Legen Sie das Ziel für die Berichtstabellen fest.
-
Mappe
- Legen Sie die Zielarbeitsmappe fest.
-
-
- <Keine>: Berichtsblatttabellen nicht ausgeben
-
-
- <Quelle>: Die Quelldatenarbeitsmappe
-
-
- <neu>: Eine neue Arbeitsmappe
-
-
- <existiert>: Eine festgelegte existierende Arbeitsmappe
-
Mappenname
- Geben Sie einen Namen für die Arbeitsmappe an.
-
Blatt
- Das Zielarbeitsblatt
-
Blattname
- Der Name des Zielarbeitsblatts
-
Spalte
-
- <neu> Statistiken in angehängten Spalten ausgeben
- <Gehe zu Quelle> Statistiken in angehängten oder eingefügten Spalten ausgeben
-
Ergebnisfenster
- Legen Sie fest, ob der Bericht im Ergebnisfenster ausgegeben wird.
-
Skriptfenster
- Legen Sie fest, ob der Ergebnis im Skriptfenster ausgegeben wird.
-
Notizfenster
- Legen Sie das Ziel des Notizfensters fest:
-
-
- <Keine>: Nicht in einem Notizfenster ausgeben
-
-
- <neu>: In ein neues Notizfenster ausgeben Legen Sie den Namen für das Notizfenster fest.
|
|