17.1.2.1 The Statistics on Rows Dialog BoxDescStatsRow-Dialog
Supporting Information
Input
Quantities
Moments
- Let
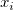 be the ith sample and be the ith sample and 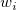 be the ith weight. be the ith weight.
| N Total
|
Total number of data points, denoted by n
|
| N Missing
|
Number of missing values
|
| Mean
|
The mean (average) score
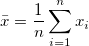 . .
|
| Standard deviation
|
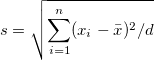
where 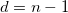
Note: In OriginPro, 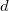 has another option, defined in the Variance Divisor of Moment branch. has another option, defined in the Variance Divisor of Moment branch.
|
| SE of Mean
|
Standard error of mean:
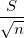
|
| Lower 95% CI of Mean
|
Lower limit of the 95% confidence interval of mean
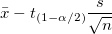
where 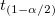 is the is the 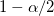 critical value of the Student's t-statistic with n-1 degrees of freedom critical value of the Student's t-statistic with n-1 degrees of freedom
|
| Upper 95% CI of Mean
|
Upper limit of the 95% confidence interval of mean
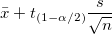
where 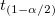 is the is the 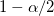 critical value of the Student's t-statistic with n-1 degrees of freedom critical value of the Student's t-statistic with n-1 degrees of freedom
|
| Variance
|
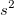
|
| Sum
|
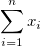 . .
|
| Skewness
|
Skewness measures the degree of asymmetry of a distribution. It is defined as
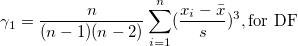
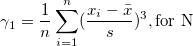
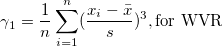
|
| Kurtosis
|
Kurtosis depicts the degree of peakedness of a distribution.
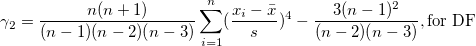
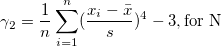
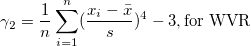
|
| Uncorrected Sum of Squares
|
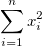
|
| Corrected Sum of Squares
|
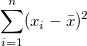
|
| Coefficient of Variance
|
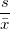
|
| Mean absolute Deviation
|
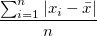
|
| SD times 2
|
Standard deviation times 2.
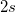
|
| SD times 3
|
Standard deviation times 3.
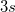
|
| Geometric Mean
|
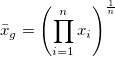
|
| Geometric SD
|
The geometric standard deviation
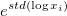 Where std is the unweighted sample standard deviation.
Where std is the unweighted sample standard deviation.
Note: Weights are ignored for the geometric standard deviation.
|
| Mode
|
The mode is the element that appears most often in the data range. If multiple modes are found, the smallest will be chosen.
|
| Harmonic Mean
|
harmonic mean (sometimes called the subcontrary mean)
without weight: 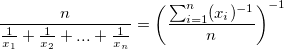
with weight: 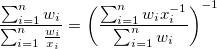
if any 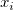 or weight is negative, return missing; if any or weight is negative, return missing; if any 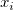 or weight is 0, return 0. or weight is 0, return 0.
|
Quantiles
Quantiles are values from the data, below which is a given proportion of the data points in a given set. For example, 25% of data points in any set of data lay below the first quartile, and 50% of data points in a set lay below the second quartile, or median.
Sort the input dataset in ascending order. Let 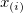 be the ith element of the reordered dataset be the ith element of the reordered dataset
| Minimum
|
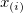
|
| Index of Minimum
|
The index number of Minimum in the original (input) dataset.
|
| 1st Quartile (Q1)
|
First (25%) quantile, Q1. See Interpolation of quantiles for computational methods.
|
| Median
|
Median or second (50%) quantile, Q2. See Interpolation of quantiles for computational methods.
|
| 3rd Quartile (Q3)
|
Third (75%) quantile, Q3. See Interpolation of quantiles for computational methods.
|
| Maximum
|
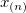
|
| Index of Maximum
|
The index number of Maximum in the original (input) dataset.
|
| Interquartile Range (Q3-Q1)
|

|
| Range (Maximum-Minimum)
|
Maximum - Minimum
|
| Custom Percentile(s)
|
Request computation of custom percentiles.
|
| Percentile list
|
This option is only available when Custom Percentile(s) is checked. Percentiles are computed for all the values listed.
|
| Median Absolute Deviation
|
For a univariate data set X1, X2, ..., Xn, the MAD is defined as the median of the absolute deviations from the data's median:
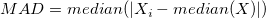
that is, starting with the residuals (deviations) from the data's median, the MAD is the median of their absolute values.
|
| Robust Coefficient of Variation
|
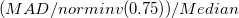
|
Computation Control
Variance Divisor of Moment
- Controls computation of variance divisor d
| DF
|
Degree of freedom
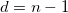
|
| N
|
Number of non-missing observations.

|
Interpolation of quantiles
- This option decides the methods for calculating Q1, Q2, and Q3.
- Let the ith percentile be y, set
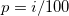 , and let , and let
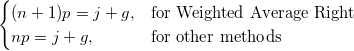
- where j is the integer part of np, and g is the fractional part of np, then different methods define the
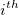 percentile, y, as described by the following: percentile, y, as described by the following:
Output
| Report Tables
|
Specifies the destination of report worksheet tables
- Book
- Specifies the destination workbook.
- <none>: Do not output report worksheet tables.
- <source>: The source data workbook.
- <existing>: A specified existing workbook
- BookName
- Enter the name of the workbook.
- Sheet
- The target worksheet.
- SheetName
- Name of the target worksheet.
- Column
- <new> Output stats to appended columns.
- <next to source> Output stats to appended or inserted columns.
- Results Log
- Output the report to the Results Log
- Script Window
- Output the report to the Script Window
- Notes Window
- Specify the destination Notes window:
- <none>: Do not output to a Notes window.
- <new>: Output to a new Notes window. Specify a name for the Notes window.
|
|