Dialog Nebeneinander angezeigte Statistik
SidebySide-Stats-Dialog 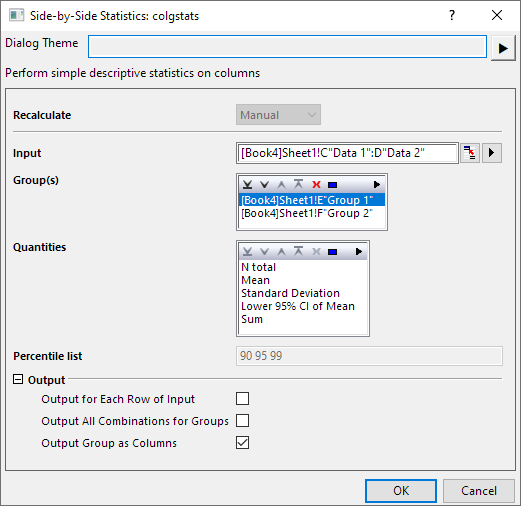
Eingabe
Legen Sie den Eingabedatenbereich fest..
Gruppen
Mehrere Gruppierungsspalten enthalten Gruppierungsinformationen, die in das Feld Gruppe eingefügt werden können. Verschiedene Gruppierungswerte weisen darauf hin, dass die Daten in den entsprechenden Zellen aus verschiedenen Gruppen sind. Sie können Gruppierungsspalten über Schaltflächen hinzufügen, entfernen und ordnen: Nach oben verschieben  , Nach unten verschieben , Nach unten verschieben  , Entfernen , Entfernen  , Alle auswählen , Alle auswählen  , Auswählen , Auswählen  auf der Symbolleiste auf der Symbolleiste  . Die Gruppierungsspalten sind auf kategorisch gesetzt, falls die meisten Spaltenwerte Text sind. Sie können die Ausgabespalten ganz einfach neu ordnen. . Die Gruppierungsspalten sind auf kategorisch gesetzt, falls die meisten Spaltenwerte Text sind. Sie können die Ausgabespalten ganz einfach neu ordnen.
Statistische Kennwerte
Angenommen, 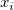 ist die ist die  -te Stichprobe und -te Stichprobe und 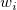 die die  -te Gewichtung. -te Gewichtung.
| N gesamt |
Gesamtanzahl der Datenpunkte, bezeichnet mit n
|
| N fehlend |
Anzahl der fehlenden Werte
|
| Mittelwert |
Der (durchschnittliche) Mittelwert
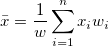 . Wenn es keine Variable Gewichtung gibt, wird die Formel reduziert auf . Wenn es keine Variable Gewichtung gibt, wird die Formel reduziert auf 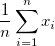 . .
|
| Standardabweichung |
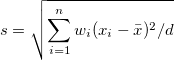
wobei 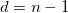
Hinweis: In OriginPro hat 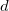 vier Optionen mehr, die im Zweig Varianzdivisor des Moments definiert sind. vier Optionen mehr, die im Zweig Varianzdivisor des Moments definiert sind.
|
| SE des Mittelwerts |
Standardfehler des Mittelwerts
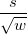
|
| Unteres 95% KI des Mittelwerts |
Untere Grenze des 95%-Konfidenzintervalls des Mittelwerts
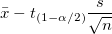
wobei 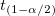 der der 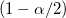 kritische Wert der Studenten-t-Statistik mit n-1 Freiheitsgraden ist. kritische Wert der Studenten-t-Statistik mit n-1 Freiheitsgraden ist.
|
| Oberes 95% KI des Mittelwerts |
Obere Grenze des 95%-Konfidenzintervalls des Mittelwerts
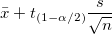
wobei 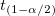 der der 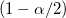 kritische Wert der Studenten-t-Statistik mit n-1 Freiheitsgraden ist. kritische Wert der Studenten-t-Statistik mit n-1 Freiheitsgraden ist.
|
| Varianz |
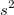
|
| Summe |
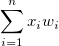 . Wenn es keine Variable Gewichtung gibt, wird die Formel reduziert auf . Wenn es keine Variable Gewichtung gibt, wird die Formel reduziert auf 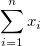 . . |
| Schiefe |
Die Schiefe misst den Grad der Asymmetrie einer Verteilung. Sie wird definiert als
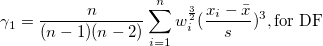
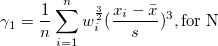
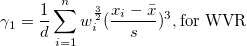
Hinweis: Wenn die WDF- oder WS-Methode ausgewählt ist, wird die Schiefe als fehlender Wert angegeben.
|
| Kurtosis |
Die Kurtosis zeigt den Grad der Peaks einer Verteilung an.
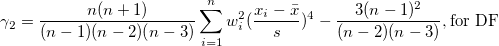
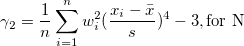
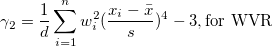
Hinweis: Wenn die WDF- oder WS-Methode ausgewählt ist, wird die Kurtosis als fehlender Wert angegeben.
|
| Unkorrigierte Summe der Quadrate |
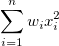
|
| Korrigierte Summe der Quadrate |
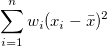
|
| Variationskoeffizient |
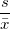
|
| Mittelwert Absolutabweichung |
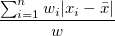
|
| SD mal 2 |
Standardabweichung mal 2
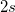
|
| SD mal 3 |
Standardabweichung mal 3
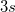
|
| Geometrischer Mittelwert |
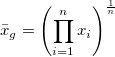
Hinweis: Gewichtungen werden für den geometrischen Mittelwert ignoriert.
|
| Geometrische StAbw |
Die geometrische Standardabweichung 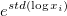 , wobei std für die ungewichtete Standardabweichung der Stichprobe steht. , wobei std für die ungewichtete Standardabweichung der Stichprobe steht.
Hinweis: Gewichtungen werden für die geometrische Standardabweichung ignoriert.
|
| Modus |
Der Modus ist das Element, das am häufigsten im Datenbereich auftaucht. Wenn mehrere Modi gefunden werden, wird das kleinste gewählt.
|
| Summe der Gewichtungen |
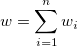
|
| Harmonisches Mittel |
Harmonisches Mittel
ohne Gewichtung: 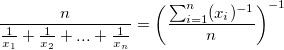
mit Gewichtung: 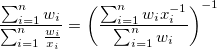
wenn 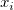 oder Gewichtung negativ ist, wird Fehlende weitergegeben; wenn oder Gewichtung negativ ist, wird Fehlende weitergegeben; wenn 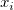 oder Gewichtung 0 ist, wird 0 weitergegeben. oder Gewichtung 0 ist, wird 0 weitergegeben.
|
| Minimum |
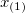
|
| Index des Minimums |
Die Indexnummer des Minimums im ursprünglichen (Eingabe-)Datensatz
|
| 1. Quartil (Q1) |
Erstes (25%) Quantil, Q1 Informationen zu Berechnungsmethoden finden Sie unter Interpolation von Quantilen.
|
| Median |
Median oder zweites (50%) Quantil, Q2 Informationen zu Berechnungsmethoden finden Sie unter Interpolation von Quantilen.
|
| 3. Quartil (Q3) |
Drittes (75%) Quantil, Q3 Informationen zu Berechnungsmethoden finden Sie unter Interpolation von Quantilen.
|
| Maximum |
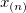
|
| Index des Maximums |
Die Indexnummer des Maximums im ursprünglichen (Eingabe-)Datensatz
|
| Interquartilbereich (Q3-Q1) |

|
| Spannweite (Maximum-Minimum) |
Maximum - Minimum
|
| Benutzerdefinierte Perzentil(e) |
Benutzerdefinierte Perzentile können berechnet werden.
|
| Perzentilliste |
Diese Option ist nur verfügbar, wenn Benutzerdefinierte Perzentil(e) aktiviert ist. Perzentile werden für alle aufgeführten Werte berechnet.
|
| Mittlere absolute Abweichung (MAD) |
Für einen univariaten Datensatz X1, X2, ..., Xn, wird MAD als Median der absoluten Abweichungen vom Median der Daten definiert:
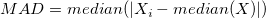
das heißt, angefangen bei den Residuen (Abweichungen) vom Median der Daten, ist die mittlere absolute Abweichung MAD der Median ihrer absoluten Werte.
|
| Robuster Variationskoeffizient |
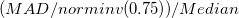
|
Ausgabe
| Ausgabe für jeder Zeile der Eingabe |
Die entsprechenden Statistiken rechts von jeder Datenzeile werden ausgegeben. |
| Ausgabe aller Kombinationen der Gruppen |
Das Statistikergebnis von jeder kombinierten Gruppe wird auf der rechten Seite der Quelldaten ausgegeben.
Hinweis:
- Wenn die Option Ausgabe für jeder Zeile der Eingabe aktiviert ist, ist diese Option nicht verfügbar.
- Wenn es zwei Gruppen gibt, zum Beispiel Gruppe1: A1, A2 und Gruppe 2: B1,B2, dann sind die Ausgabegruppen A1-B2, A1-B2, A2-B1,A2-B2. Auch wenn es kein A1-B2 in den Quelldaten gibt, wird es als eine Zeile ausgegeben.
|
| Gruppen als Spalten ausgeben |
Die Gruppeninformationen zu den Spalten werden ausgegeben. |
|