Algorithmus

 

Inhalt

Shapiro-Wilk-Test auf Normalverteilung

Bei einem gegebenen Satz von Beobachtungen 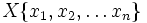X\{x_1,x_2,\ldots x_n\}, der entweder in aufsteigender oder absteigender Reihenfolge sortiert ist, wird die Shapiro Wilk W-Statistik definiert als:

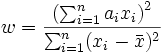
w=\frac{\left (\sum_{i=1}^n a_ix_i\right)^2}{\sum_{i=1}^n (x_i-\bar{x})^2}

wobei

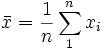
\bar{x}=\frac{1}{n}\sum_{1}^n x_i

der Stichprobenmittelwert ist und ai, für i=1, 2,...n ein Satz von mathematischen Gewichtungen, deren Werte nur von der Stichprobengröße n abhängen.

Der Algorithmus, der von Origin verwendet wird, stammt aus dem von Patrick Royston beschriebenen Applied Statistics Algorithm R94 (1995). Die Funktion unterstützt Stichprobenumfänge von 3.

Der Freiheitsgrad (DF) ist gleich der Stichprobengröße.

Kolmogorov-Smirnov-Test auf Normalverteilung

Origin ruft eine NAG-Funktion auf, nag_1_sample_ks_test (g08cbc), um die Statistik zu berechnen. Bitte lesen Sie weitere Einzelheiten zu dem Algorithmus im entsprechenden NAG-Dokument nach.

Lilliefors-Test auf Normalverteilung

Der Lilliefors-Test ist eine Adaption des Kolmogorov-Smirnov-Tests. Die Statistik wird auf dieselbe Weise berechnet wie die Statistik des Kolmogorov-Smirnov-Tests. Der p-Wert ist jedoch unterschiedlich, da der Lilliefors-Test den Mittelwert und die Varianz der Daten nicht berücksichtigt, während der Kolmogorov-Smirnov-Test das tut. Die Methode nach Dallal und Wilkinson (1986) wird für die Berechnung des p-Werts verwendet.

Anderson-Darling-Test

Bei einem gegebenen Satz von Beobachtungen 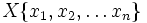X\{x_1,x_2,\ldots x_n\}, der in aufsteigender Reihenfolge sortiert ist, wird die Anderson-Darling-Statistik definiert als:

A2 = - n - S

wobei

S=\sum_{i=1}^n \frac{2i-1}{n}[lnF(x_i)+ln(1-F(x_n+1-i))]

F ist die kumulative Verteilungsfunktion der F-Verteilung.

D'Agostino-K

  • Schiefe-Statistik
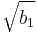    1. Die Schiefe \sqrt{b_1} aus den Daten berechnen
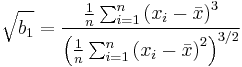
      \sqrt{b_1}= \frac{\frac{1}{n} \sum_{i=1}^n \left( x_i - \bar{x} \right)^3}{\left( \frac{1}{n} \sum_{i=1}^n \left( x_i - \bar{x} \right)^2 \right)^{3/2}}
    2. Berechnen
      Y=\sqrt{b_1}[\frac{(n+1)(n+3)}{6(n-2)}]^{1/2}
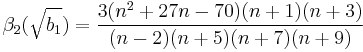      \beta_2(\sqrt{b_1})=\frac{3(n^2+27n-70)(n+1)(n+3)}{(n-2)(n+5)(n+7)(n+9)}
      W^2=-1+[2(\beta_2(\sqrt{b_1})-1)]^{1/2}
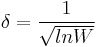      \delta=\frac{1}{\sqrt{lnW}}
      \alpha=[\frac{2}{(W^2-1)}]^{1/2}
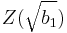    3. Die Schiefe-Statistik Z(\sqrt{b_1}) kann mit unten stehender Gleichung berechnet werden.
      Z(\sqrt{b_1}) = \delta ln(Y/\alpha+[(Y/\alpha)^2+1]^{1/2})
  • Kurtosis-Statistik
    1. Die Kurtosis b2 aus den Daten berechnen
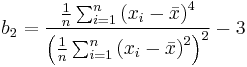
      b_2 = \frac{\frac{1}{n} \sum_{i=1}^n \left( x_i - \bar{x} \right)^4}{\left( \frac{1}{n} \sum_{i=1}^n \left( x_i - \bar{x} \right)^2 \right)^2} - 3
    2. Den Mittelwert und die Varianz von b2 berechnen
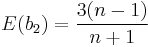      E(b_2)=\frac{3(n-1)}{n+1}
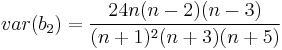
      var(b_2)=\frac{24n(n-2)(n-3)}{(n+1)^2(n+3)(n+5)}
    3. Das standardisierte Moment of b2 berechen
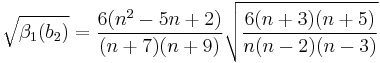
      \sqrt{\beta_1(b_2)}=\frac{6(n^2-5n+2)}{(n+7)(n+9)}\sqrt{\frac{6(n+3)(n+5)}{n(n-2)(n-3)}}
    4. Berechnen
      A=6+\frac{8}{\sqrt{\beta_1(b_2)}} [\frac{2}{\sqrt{\beta_1(b_2)}}+\sqrt{1+\frac{4}{\beta_1(b_2)}}]
    5. Die Kurtosis-Statistik Z(b2) kann mit unten stehender Formel berechnet werden.
      Z(b_2)=((1-\frac{2}{9A})-[\frac{1-2/A}{1+x\sqrt{2/(A-4)}}]^{1/3})/\sqrt{2/(9A)}
  • D'Agostino's Chi2 Statistic
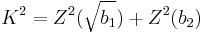
    K^2 = Z^2(\sqrt{b_1})+Z^2(b_2)

Chen-Shapiro-Test

Bei einem gegebenen Satz von Beobachtungen 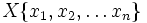X\{x_1,x_2,\ldots x_n\}, der in aufsteigender Reihenfolge sortiert ist, wird Chen-Shapiro-Statistik definiert als:

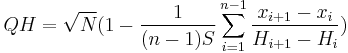
QH =\sqrt{N}(1-\frac{1}{(n-1)S}\sum_{i=1}^{n-1}\frac{x_{i+1}-x_i}{H_{i+1}-H_i})

wobei

Hi = - 1((i - 3 / 8) / (n + 1 / 4)) und - 1 sind die Inverse der Standardnormalverteilung.

 
English | Deutsch | 日本語