15.3.5.2 Global Fitting with Parameter SharingGlobalFitting-Param-Sharing
Global fitting in Origin involves fitting multiple datasets with the same fitting function. Parameters in the fitting function can optionally be shared amongst all datasets. If a parameter is shared, the fitting procedure will yield the same value for that parameter for all datasets. If a parameter is not shared, the fitting procedure will yield a unique value for that parameter for each dataset.
Key points of Global Fitting:
- Multiple datasets are fitted with one model simultaneously.
- Fit parameters are optionally shared between the datasets.
- For each shared (global) parameter, one best-fit value is estimated from all of the datasets that are fitted.
- For each non-shared (local) parameter, a unique best-fit value is generated for individual dataset that is fitted.
- Other options such as constraints and weighting are also available when you choose to perform Global Fitting.

To do global fitting with parameter sharing:
- Select multiple datasets when you open the NLFit dialog.
- Select a fitting function.
- In the Data Mode drop-down list of Data Selection settings, select Global Fit.
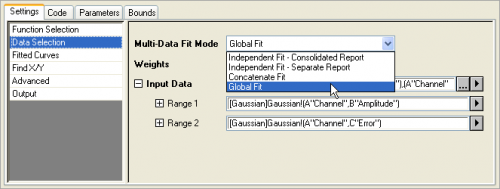 - In the Parameters tab, select the checkbox in the Share column which corresponds to the parameter you want to set as shared.
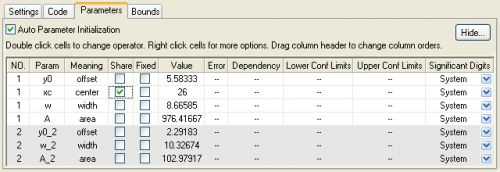
- Click the Fit or OK button to perform the fitting.
Related Algorithm
The fitting report for global fit will output the Parameters, Statistics and ANOVA tables for each dataset and a global Statistics and ANOVA table for all of the datasets. When global fitting is performed, the Chi-square for n datasets is computed as:
![\chi ^2=\sum_{i=1}^m[\frac{Y1_i-f(x1_i^{\prime };\hat \theta 1)}{\sigma 1_i}]^2+\sum_{i=1}^m[\frac{Y2_i-f(x2_i^{\prime };\hat \theta 2)}{\sigma 2_i}]^2+\ldots +\sum_{i=1}^m[\frac{Yn_i-f(xn_i^{\prime };\hat \theta n)}{\sigma n_i}]^2 \chi ^2=\sum_{i=1}^m[\frac{Y1_i-f(x1_i^{\prime };\hat \theta 1)}{\sigma 1_i}]^2+\sum_{i=1}^m[\frac{Y2_i-f(x2_i^{\prime };\hat \theta 2)}{\sigma 2_i}]^2+\ldots +\sum_{i=1}^m[\frac{Yn_i-f(xn_i^{\prime };\hat \theta n)}{\sigma n_i}]^2](//d2mvzyuse3lwjc.cloudfront.net/doc/en/UserGuide/images/Global_fitting_with_parameter_sharing/math-1f3cb19d3a7b4783b74da7037ddc8af0.png?v=0)
and
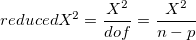
The global ANOVA table is:
|
|
df
|
Sum of Squares
|
Mean Square
|
F Value
|
Prob > F
|
| Model
|
p-1
|
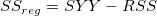
|

|
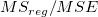
|
p-value
|
| Error
|
-p
|
RSS
|
MSE = RSS /(n-p)
|
|
|
| Total
|
n-1
|
SYY
|
|
|
|
In the above formula, n is the total number of data points, and p is the total number of parameters. Note that when parameters are shared, it will reduce the number of parameters, p. For example, to do a global fit for two datasets with simple linear function, y = a + bx, with the parameter a shared, the number of parameters becomes three because we have reduced one parameter. Therefore, p = 3.
|