フィット処理-収束, 許容値, 依存
非線形フィット処理は、反復計算を行います。2つの連続する既約カイ二乗値の差がある許容値より小さくなるまで、処理が続けられます。処理が完了したら、フィットが収束したということです。1つのパラメータを持つモデルを使って、これを説明します。
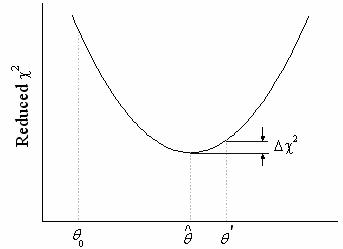
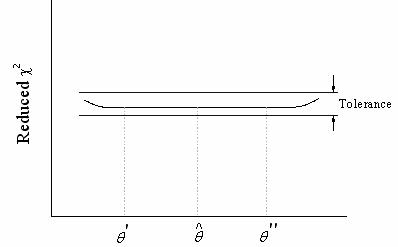
曲線は、フィット処理中の既約 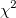 値の変化を表しています。初期値 値の変化を表しています。初期値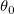 から開始して、 パラメータ値が計算され、 から開始して、 パラメータ値が計算され、 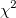 値が縮小されます。フィットは 値が縮小されます。フィットは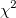 許容値になったときに収束します。 許容値になったときに収束します。
非線形曲線フィット処理の目的は、既約 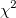 値の絶対値の最小値を見つけることです。しかし、この最小化の処理が絶対最小値にならない場合があります。これは、フィットが収束しないということです。フィットが収束しない場合、次のいずれかを行うことで原因を見つけられる場合があります。 値の絶対値の最小値を見つけることです。しかし、この最小化の処理が絶対最小値にならない場合があります。これは、フィットが収束しないということです。フィットが収束しない場合、次のいずれかを行うことで原因を見つけられる場合があります。
パラメータの初期値に問題がある
初期値はフィット処理によって大変重要です。これらは、今まで行った分析からの経験的な値であったり、関数式を近似的な形式に変換して推定した値にすることができます。良い初期値を使うと、フィット実行の時間を削減できます。
相対最小値と絶対最小値
反復計算において、絶対的(つまり、大域的あるいはグローバル)ではなくむしろ相対的(つまり、局所的あるいはローカル)な最小値(つまり、極小値)が見つかることがよくあります。その場合、既約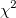 の値をそれ以上減少させることができず、フィット処理は実質的に収束してしまいます。 の値をそれ以上減少させることができず、フィット処理は実質的に収束してしまいます。
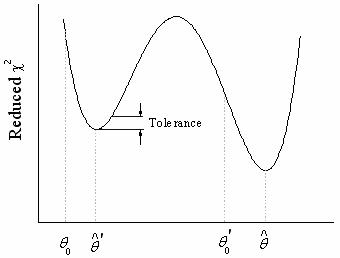
その最大の問題は、求められた最小値が実際に相対的なものか絶対的ものかが、分からないということです。 反復計算で、絶対的な最小値が求められたかどうかを唯一確認する方法は、幾つかのパラメータの値からフィットをしてみて、その結果を観察するということだけです。もし、常に同じ最終結果が得られれば、それが局所的な極小値であることは無いと判断して良いでしょう。
パラメータ値が変化し続ける場合
非線形フィットで最もよく起こる問題は、初期値の選択に関わらず、全てあるいは一部のパラメータが反復計算の過程において変化し続け、 収束せず、発散してしまい、その結果、数値のオーバフロー又はアンダーフローが起こることです。これは、使用するフィット関数やデータに対して、注意を払うことが必要だということです。また、データに最適にフィットするパラメータの値は単に1組とは限らず、いくつかの値であることもあります。
関数の過剰パラメータ化
関数のパラメータが、独立変数に関して同じ微分を持つ場合、その関数は過剰パラメータ化になっている可能性があります。このような場合、フィット処理は収束しません。例えば、過剰パラメータの典型的な例として、次のようなものがあります。
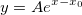
A は、振幅で、x0 は水平オフセットです。上の関数を次のように書き直してみましょう。
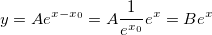
つまり、フィットにおいて、B=A*exp(-x0) が同じ値になるように A と 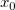 の組合わせを変化させると、 既約 の組合わせを変化させると、 既約 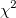 の値は変化しません。これ以上フィットの手段を向上しようとする試みは時間の無駄です。 の値は変化しません。これ以上フィットの手段を向上しようとする試みは時間の無駄です。
問題の発生を示す次の2つの単純な兆候があります。
- パラメータの誤差の値が、パラメータ値自体に比べ相対的に非常に大きい場合。例えば、ガウス関数のフィット処理が収束せず、幅が0.5でその誤差が10になったとすると、その幅に対する結果には意味がありません。
- (1つあるいは2つ以上の)パラメータの依存度が1に非常に近い場合。 この状況は、依存度が1に近いパラメータに関してフィットがパラメータ(又はその組合わせ)に対し依存しないようにパラメータを削除するか、固定にします。
しかし、過剰パラメータは、モデルのパラメータが物理的な意味を持たないという意味ではありません。無限に解があり、フィット処理で制約条件を付けるべきだということを提案するものです。
不適なデータ
関数が理論的には過剰パラメータ化されていない場合でも、全て又は一部のパラメータを決定するデータの情報が充分でない場合には、反復手続が過剰パラメータ化されているかのように振る舞うことがあります。これは、独立変数のデータが限られた範囲内でのみ利用可能な時によく起こります。例えば、ガウス関数のような非単調な関数を単調なデータにフィットしようとすると、データはガウス関数のピークの片側だけを使うので非線形最小二乗フィット機構は中心の位置やピークの幅の決定に困難をきたします。
|