Gridding-Methoden für Daten mit zufälligem AbstandGridMethod-RandomSpaced
Wenn Ihre Arbeitsblattdaten in den X- und Y-Dimensionen nicht über äquidistant angeordnete Abstände verfügen, sollten Sie eine der fünf Gridding-Methoden von Origin für XY-Daten mit zufälligen oder nicht äquidistanten Abständen verwenden:
Renka-Cline
Diese Gridding-Methode basiert auf dem Algorithmus, den Renka und Cline 1984 entwickelten. Der Ablauf der grundlegenden Schritte ist folgender:
- Triangulation Es wird eine Triangulation der XY-Daten durchgeführt. Die Dreiecke sind so gleichwinklig wie möglich.
- Gradientenschätzung Schätzt einen Gradienten in den X- und Y-Richtungen für jeden Knotenpunkt als teilweise Ableitung einer quadratischen Funktion.
- Interpolation Berechnet für einen beliebigen Punkt P den interpolierten Wert mit Hilfe der Datenwerte und der geschätzten Gradienten an jedem der drei Eckpunkte des Dreiecks, das P enthält.
Im Fall von 200~1000 äquidistant verteilten Datenpunkten ist die Renka-Cline-Methode eine gute Wahl.
Shepard
Diese Methode bringt die von Franke und Nielson beschriebene modifizierte Shepard-Gridding-Methode zum Einsatz. Hierbei handelt es sich um eine abstandsbasierte Gridding-Methode mit Gewichtung, die Daten, wie folgt, interpoliert: 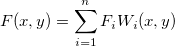 , ,
wobei 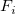 die zugrunde liegende Funktion bei den Knoten ( die zugrunde liegende Funktion bei den Knoten (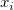 , , 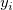 ) und ) und 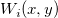 die Gewichtungen sind. Um die Berechnung zu lokalisieren, werden die Gewichtungen sind. Um die Berechnung zu lokalisieren, werden 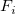 und und 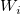 durch die Datenpunkte, die im Kreis mit dem Mittelpunkt ( durch die Datenpunkte, die im Kreis mit dem Mittelpunkt (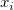 , ,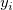 ) und einem Radius ) und einem Radius 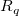 bzw. bzw. 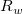 liegen, berechnet. liegen, berechnet. Zu Beginn werden die Gewichtungen definiert als: 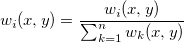 . .
Bei einem gegebenen Radius 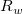 ist das relative Gewicht ist das relative Gewicht 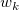 : : ![w_k=[\frac{(R_w-d_k)_{+}}{R_wd_k}]^2 w_k=[\frac{(R_w-d_k)_{+}}{R_wd_k}]^2](//d2mvzyuse3lwjc.cloudfront.net/doc/de/UserGuide/images/Gridding_Methods_for_Randomly_Spaced_Data/math-0e141a3a2c838ddf192009baaf5116ad.png) für für
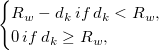
und 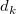 ist die Euklidische Distanz zwischen (x, y) und ( ist die Euklidische Distanz zwischen (x, y) und (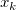 , , 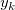 ): ): 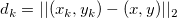 . .
Für jeden 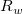 > 0 haben wir: > 0 haben wir: 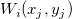 = =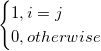
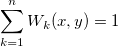 . .
Als nächstes wird die Knotenfunktion 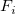 durch eine lokale Approximationsfunktion durch eine lokale Approximationsfunktion 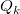 ersetzt. ersetzt. 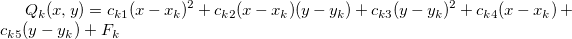
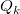 ist die gewichtete Approximationsfunktion der kleinsten Quadrate zu den Daten, die innerhalb von ist die gewichtete Approximationsfunktion der kleinsten Quadrate zu den Daten, die innerhalb von 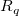 der Knotenpunkte liegen. Die Koeffizienten minimieren also: der Knotenpunkte liegen. Die Koeffizienten minimieren also:
![\varepsilon _k=\sum_{i=1,j\neq k}^N\omega _i(x_k,y_k)[c_{k1}(x_i-x_k)^2+\ldots +c_{k5}(y_i-y_k)+F_k-F_i]^2 \varepsilon _k=\sum_{i=1,j\neq k}^N\omega _i(x_k,y_k)[c_{k1}(x_i-x_k)^2+\ldots +c_{k5}(y_i-y_k)+F_k-F_i]^2](//d2mvzyuse3lwjc.cloudfront.net/doc/de/UserGuide/images/Gridding_Methods_for_Randomly_Spaced_Data/math-8ab8ecc395dfc1db378345af3deb4929.png)
für ![\omega _i(x,y)=[\frac{(R_q-d_i)_{+}}{R_qd_i}]^2=[\frac{(R_q-||(x_i,y_i)-(x,y)||_2)_{+}}{R_q||(x_i,y_i)-(x,y)||_2}]^2 \omega _i(x,y)=[\frac{(R_q-d_i)_{+}}{R_qd_i}]^2=[\frac{(R_q-||(x_i,y_i)-(x,y)||_2)_{+}}{R_q||(x_i,y_i)-(x,y)||_2}]^2](//d2mvzyuse3lwjc.cloudfront.net/doc/de/UserGuide/images/Gridding_Methods_for_Randomly_Spaced_Data/math-82914bba8b91c96a6d5fe1c5865f7fe6.png) . .
Oben ist zu sehen, dass die Interpolationsfunktion eine lokale Approximationsfunktion ist und vom Einflussradius der Knotenpunkte 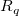 und und 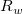 abhängt. Zwei ganze Zahlen, abhängt. Zwei ganze Zahlen, 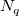 und und 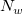 , werden verwendet, um , werden verwendet, um 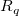 und und 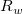 zu berechnen (dies sind die Parameter q und w der Funktion und werden als Lokalitätsfaktoren der quadratischen Interpolation bzw. Lokalitätsfaktoren der Gewichtsfunktion bezeichnet): (weitere Informationen finden Sie in dem Abschnitt unter "Der Dialog XYZ-Gridding" weiter hinten.) zu berechnen (dies sind die Parameter q und w der Funktion und werden als Lokalitätsfaktoren der quadratischen Interpolation bzw. Lokalitätsfaktoren der Gewichtsfunktion bezeichnet): (weitere Informationen finden Sie in dem Abschnitt unter "Der Dialog XYZ-Gridding" weiter hinten.) 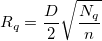 und und 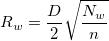 , ,
wobei n die Anzahl der Datenpunkte und D der maximale Abstand zwischen zwei Datenpunkten ist. Also können 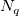 und und 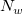 als die durchschnittliche Anzahl der Datenpunkte betrachtet werden, die - für jeden Knotenpunkt entsprechend - innerhalb den Abständen zwischen als die durchschnittliche Anzahl der Datenpunkte betrachtet werden, die - für jeden Knotenpunkt entsprechend - innerhalb den Abständen zwischen 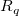 und und 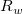 liegen. liegen. Die Berechnung wird durch Erhöhen der Werte 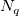 und und 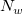 globaler; entsprechend wird die Berechnung lokaler, wenn ihre Werte verringert werden. Allgemein kann man sagen, dass da Einstellen von globaler; entsprechend wird die Berechnung lokaler, wenn ihre Werte verringert werden. Allgemein kann man sagen, dass da Einstellen von 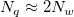 gut funktioniert. Standardmäßig gut funktioniert. Standardmäßig 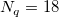 und und 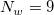 . Die folgenden Einschränkungen müssen jedoch berücksichtigt werden: . Die folgenden Einschränkungen müssen jedoch berücksichtigt werden: 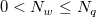 . . Der Dialog XYZ-Gridding ruft die NAG-Bibliothek auf, um die Gridding-Methode von Shepard durchzuführen. Origin bietet außerdem die auf X-Funktionen basierenden Gridding-Methoden nach Shepard xyz_shep_nag and xyz_shep, die diese Methode anhand von 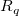 und und 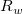 ausführen. ausführen.
Thin-Plate-Spline (TPS)
Diese Funktion bietet eine Methode für die Konvertierung einer Zufallsmatrix basierend auf dem Algorithmus Thin-Plate-Spline (TPS). Thin-Plate-Spline ist eine physikalische Interpolationsmethode. Um Gridding-Daten zu erzeugen, unterstellt diese Methode, dass alle Datenpunkte auf einer dünnen, elastischen Ebene oder einem Spline verteilt sind. Die Ebene ist an den Gitterpunkten begrenzt und formt durch Umspannen der Gitterpunkte eine zweidimensionale Oberfläche. Die Oberfläche ist zwischen den Punkten verformt, um eine wahrscheinliche Anpassung an die Daten anzuzeigen. Die besten Ergebnisse werden erzielt, indem man die so genannte “Biegungsenergiefunktion” des Spline minimiert. Da diese Methode die Minimierung der Biegungsenergie erfordert, ist es umso besser, je weniger die Ebene verbogen ist. Diese Berechnung ist der minimalen Kurvenberechnung ähnlich. Oberflächendiagramme, die durch TPS-Gridding erstellt wurden, können einen höheren Grad an Glättung aufweisen als Diagramme, die durch andere Methoden entstanden sind. Daher ist diese Methode am meisten für die Interpolation von lokal flachen Oberflächen geeignet. Die mathematische Beschreibung des TPS-Algorithmus ist bei gegebener Biegungsenergiefunktion: 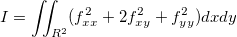 , ,
und die Minimierungsfunktion ist: 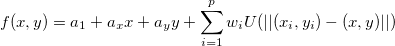 , ,
wobei 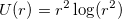 . . Zum Durchführen von TPS-Gridding muss der Glättungsparameter festgelegt werden, der die Glättung der interpolierten Oberfläche kontrolliert, und der Extrapolationsparameter, der auf die Matrixzellenwerte, die außerhalb des Originaldatenbereichs liegen, Einfluss nimmt. Weitere Einzelheiten zu TPS finden Sie unter Donato und Belongie, Approximationsmethoden für Thin Plate Spline Mappings und Principal Warps.
Zufällig (Kriging-Korrelation)
Kriging -- benannt nach dem Bergbauingenieur D. G. Krige -- ist eine bewährte geostatistische Methode zum Interpolieren von räumlichen Daten. Diese Technik ist eine gewichtete Interpolation (Extrapolation) des Gleitenden Durchschnitts, die die geschätzte Varianz eines vorhergesagten Punktes (Gitterpunkte) mit dem gewichteten Durchschnitt der umliegenden Punkte minimiert. Der gewichtete Wert wird von der räumlichen Korrelationsstruktur der ursprünglichen Daten bestimmt. Dieser Algorithmus benötigt ein Modell der räumlichen Kontinuität oder Abhängigkeit. Üblicherweise wird der Vorgang in zwei Schritte geteilt:
- Zuerst werden Semivariogramme der zu schätzenden regionalisierten Variablen erzeugt. Origin berechnet die Abstandsinformationen, erstellt eine Tabelle mit den Werten der Semivarianz und gewichtet die Semivarianzdaten. Dieses Semivariogramm beschreibt die zunehmende Differenz oder sich verringernde Korrelation zwischen Proben im Eingabedatensatz.
- Als Nächstes wird dieses Abhängigkeitsmodell zur Berechnung des Wertes des räumlichen Punkts von z verwendet.
Bei der Durchführung von Kriging kann der Vorgang durch Konfiguration der folgenden Parameter kontrolliert werden:
- Glättung: Kontrolliert die Genauigkeit der Interpolation.
- Mindestpunkte: Legt die Mindestanzahl der Kontrollpunkte fest, die zur Berechnung von z erforderlich sind.
- Suchradius: Bestimmt den Satz der in der Nähe liegenden Kontrollpunkte, die zur Berechnung von z verwendet werden.
Weitere Einzelheiten zu Kriging finden Sie unter Stein, Interpolation von räumlichen Daten.
Gewichteter Durchschnitt
Die Methode Gewichteter Mittelwert ist ein einfaches gewichtetes Mittel der Punkte mit der Gewichtung 1/r, wobei r die Entfernung eines jeden Datenpunktes von der Zelle innerhalb des Suchradius ist. Wenn keine Werte innerhalb des Suchradius liegen, wird der Radius vergrößert, bis zumindest ein Punkt getroffen wird. Das Vergrößern des Suchradius bedeutet, dass jeder Punkt in einer größeren Wechselbeziehung mit benachbarten Punkten steht, woraus eine höhere Glättung resultiert, so dass feinere Details womöglich verloren gehen.
|