Ｒコンソールを使ったOriginでのデータ分析

Ｒコンソールを使ったOriginでのデータ分析

Origin2016からＲコンソールとRserveコンソールツールが追加されました。これらを使って、RからOriginにデータを簡単に転送でき、Originの優れたグラフ作成機能を利用することが出来ます。また、Rコンソールダイアログとコマンドを使って、様々な範囲の統計機能やパッケージにRからアクセスして、Originで作成したデータを分析することが出来ます。 統計データの分析シミュレーション向けに、Rコンソールの自由なアプリケーションを表示出来る視覚化サンプルをいくつか提供しています。

パッケージのインストール

これらのサンプルを実行するために、コンピュータにＲをインストールして、bootとGenSA というRパッケージをダウンロードします。Ｒのメインウィンドウを開き（OriginのRコンソールではありません）、次のスクリプトを実行してダウンロードしてください。 

install.packages("boot")
install.packages("GenSA")
library(boot)
library(GenSA)

Bootstrapを使って相関係数を計算

Rパッケージのbootでは、bootstrapの容易な生成と統計分析の実行が行えます。このサンプルでは、このパッケージでのbootstrapを使って、相関係数をRコンソールで計算します。

  1. 新規のワークブックを作成し、単一ASCIIのインポート Button Import Single ASCII.pngをクリックして、\OriginLab\Origin2016\Samples\StatisticsからLogRegData.datをインポートします。
  2. メインメニューから接続：Ｒコンソールを選択してＲコンソールダイアログを開きます。
  3. Select.png ボタンをクリックして、ワークシートにある最初の２列を選択します。データをデータフレームに設定し、Ｒオブジェクトボックスのオブジェクト名をdataと入力します。Send data.pngボタンをクリックして、データをOriginからRのスペースに移動します。
    Send data rconsole.png
  4. 次に、下のスクリプトをＲコンソールのスクリプトインボックスで実行します。ボックスに貼り付けてEnterをクリックして実行します：
library(boot)
f <- function(d, i){
d2 <- d[i,]
return(cor(d2$Age, d2$Salary))
}
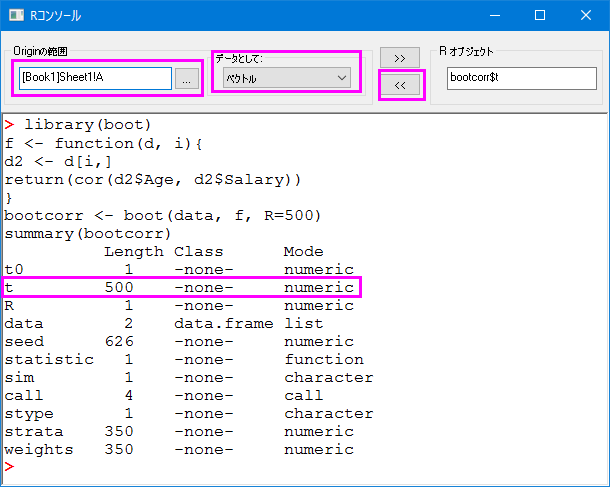
bootcorr <- boot(data, f, R=500)
summary(bootcorr)

5. 計算結果は、Rオブジェクトbootcorrに保存され、bootstrapそれぞれの相関はbootcorr$tに保存されます。次に新しいワークブックを作成し、Get data.png をクリックして、R オブジェクトbootcorr$tをA列にベクトルで入力します。A列に結果の500行の結果データが入力されます。

Get data rconsole.png

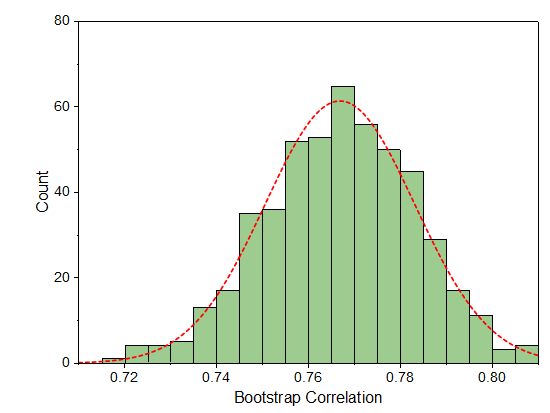
6. A列をクリックして、作図：統計：ヒストグラムを選択し、ヒストグラムを作成します。次に、分布曲線の作図を行い色を編集すると、下図のグラフが得られます。

Bootstrip.png


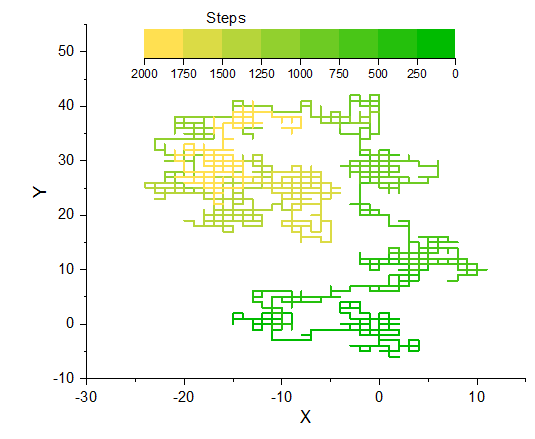
2D格子のランダムウォークをシミュレート

Ｒでは、ランダムサンプルと行列操作の効率的な機能があります。ここでは、Rでランダムウォークデータを生成し、Originの色付き折れ線でルートを示したランダムウォークの例を実演します。

  1. 3つの列がある新規のワークブックを作成します。
  2. メインメニューの接続：Ｒコンソールを選択して、ダイアログを開き、次のランダムウォーク生成のスクリプトを実行します：
step <- 2000
walk <- matrix(0, ncol = 3, nrow=step)      
index <- cbind(seq(step), sample(c(1, 2), step, TRUE))
walk [index] <- sample(c(-1, 1), step, TRUE)
walk [,1] <- cumsum(walk[, 1])
walk [,2] <- cumsum(walk[, 2])
walk [,3] <-seq(step)

Enterを押してスクリプトを実行します。

3. [Book1]Sheet1!A:CにＲオブジェクトを行列として送ります。

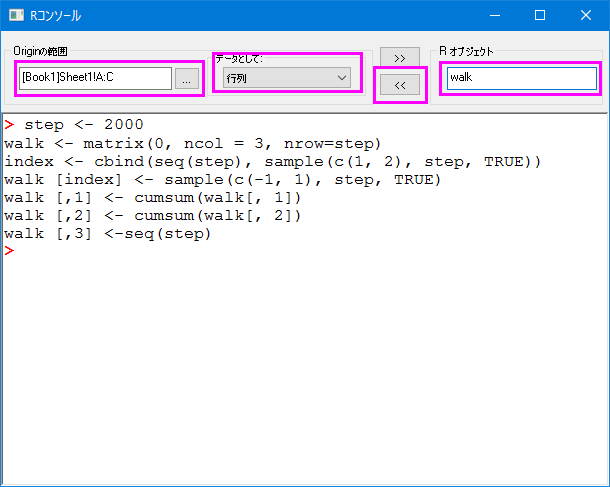
Send data rconsole rwk.png

4. Book1のsheet1にある列Bを選択して折れ線を作成します。列Ｃのデータは線の色を制御に使い、カラースケールと色調を編集します。

Randomwork.png

グローバル最小値の検索をアニーリングでシミュレート

サンプルを実行する前に、 GenSAパッケージをインストールします。

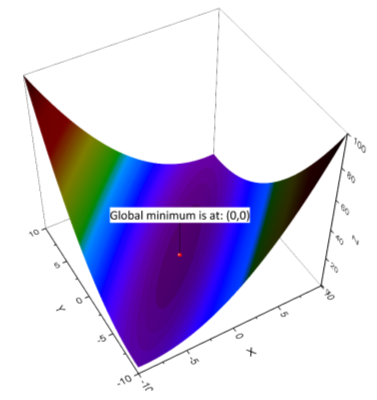
アニーリングシミュレーションは、非線形曲線で発生する問題のグロ―バルな最小値を見つける方法です。ここでは、ＲでGenSAパッケージを使って、テスト関数でのアニーリングシミュレーションを実行し、範囲内X,Y\in [-10,10]のＺ最小値を検索します。

z=0.26(x^2+y^2)-0.48xy

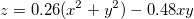
Ｒで計算した後、結果データをOriginに送り、等高線を作成して結果を可視化します。また、それぞれの移動ステップで折れ線を作成し、取得される最小値を検出します。

1. メインメニューから接続：Rコンソールを選択し、スクリプトボックスに次のスクリプトを入力して、Enterを押して実行します。 

fr <- function(vx){
x <- vx[1]
y <- vx[2]   
0.26*(x^2+y^2)-0.48*x*y}
set.seed(25)
dimension <-2
global.min <- 0
tol <- 1e-13
lower <- c(-10,-10)
upper <- c(10,10)
out <- GenSA(lower = lower, upper = upper, fn = fr,
control=list(temperature=200,threshold.stop=global.min+tol,verbose=TRUE,max.call=1E3))
#output the results
sprintf("Global minima for the function is: %.3f at (%.3f, %.3f)", out$value, out$par[1],out$par[2])

結果の出力は： 

[1] 「この関数でのグローバル最小値: 0.000 at (0.000, 0.000)"

最小ポイントと一緒に等高線を作成するには：

2. 標準ツールバーの3D関数グラフ ボタンButton New 3D Plot.pngをクリックし、次のグラフの様に関数を設定します：

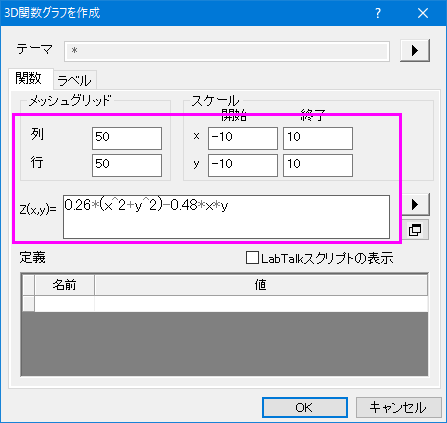
Func plot r.png

3. OKをクリックして、3D曲面図を作成します。作図の詳細 カラーマップ タブでカラーマップを指定することが出来ます。.
4. 新規のワークブックを作成し、列を3つ作って、それぞれの列属性をXYZにします。最初の行に(0,0,0) を入力して、作成した3Dグラフに列を選択してドラッグでグラフに挿入します。1つの散布図ポイントがグラフに追加されますので、作図の詳細 ラベルタブで、散布図にラベルテキストを追加編集します。

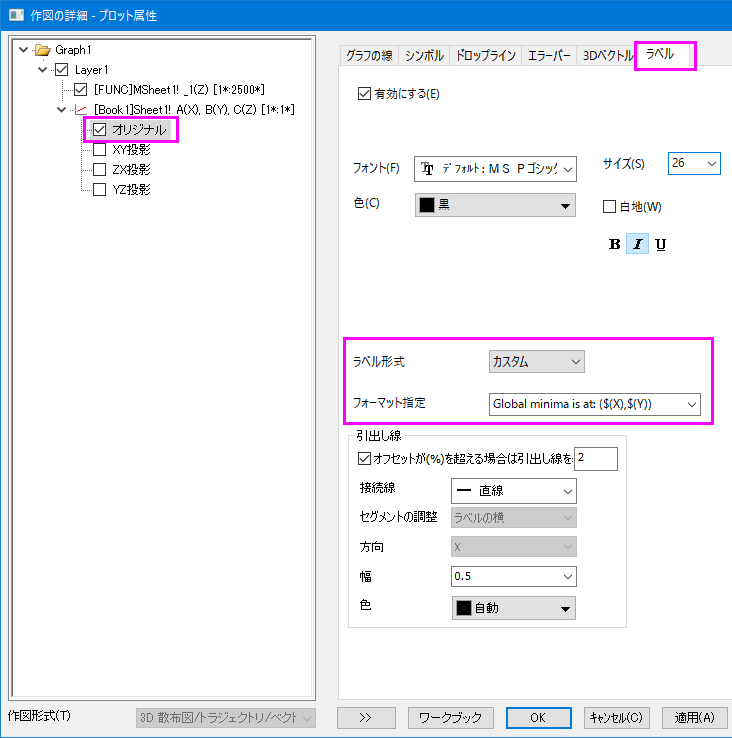
Minimum label.png

完成したグラフは次のようになります。

Minimum.png

MANOVE分析

このサンプルでは、看護グループでの労働費について、多変量解析を実行してみます。 2つの予測値：所有権と認可、3つの従属変数：看護労働費、ハウスキーピング労働費、メンテナンス費用があります。異なる所有権と認可では労働費も異なるのかどうかを知るために、ＲコンソールのデータでMANOVAを実行します。

  1. LaborCost.zipからデータをダウンロードし、解凍してLaborCost.datを入手します。Originで新規のワークブックを開き、ドラッグ＆ドロップでこのデータをOriginにインポートしてください。
  2. Select.png ボタンをクリックして、ワークシートにある全ての5列を選択します。データをデータフレームに設定し、Ｒオブジェクトボックスのオブジェクト名をCostDataと入力します。Send data.pngボタンをクリックして、データをOriginからRのスペースに移動します。
  3. 入力ボックスでRスクリプトを実行
Cost<-data.matrix(CostData[,3:5])
Ownership<-CostData[,1]
Certification<-CostData[,2]
fit <- manova(Cost ~ Ownership*Certification)
summary(fit, test="Pillai")

データフレームに入れる結果を入れ替えることが出来ます。dfをOriginのワークシートにデータフレームとして渡します。 

sum<-summary(fit, test="Pillai")
df<-as.data.frame(sum$stats)
Manova df.png

所有権のＰ値が0.01よりも小さいので労働費の平均に影響する所有権はないと考えられます。 しかし、認定のＰ値が0.089なので結果がほぼ有意であることを示し、3タイプの認定での労働費の平均はそれぞれ異なる可能性があります。

English | Deutsch | 日本語