t-Test bei einer Stichprobe
tTest-OneSample
Einführung
Ein Studenten t-Test bei einer Stichprobe bestimmt, ob der Mittelwert einer Stichprobe, die einer normalverteilten Grundgesamtheit entstammt, einem hypothetischen Wert bei gegebenem Konfidenzniveau entspricht. Indem Sie einen ein- oder beidseitigen t-Test wählen, können Sie überprüfen, wie wahrscheinlich es ist, dass der Stichprobenmittelwert größer, kleiner oder gleich dem wahren Mittelwert der Grundgesamtheit ist. Beachten Sie, dass der t-Test bei einer Stichprobe angemessen ist, wenn die Standardabweichung der gesamten Grundgesamtheit unbekannt ist.
Der Wert der t-Statistik und der p-Wert werden berechnet, um zu entscheiden, ob die Nullhypothese zurückgewiesen wird oder nicht. Der p-Wert ist die Wahrscheinlichkeit, dass die Nullhypothese wahr ist. Ein kleiner p-Wert weist darauf hin, dass Sie sie zurückweisen sollten.
Das Konfidenzintervall hat untere und obere Grenzen für den möglichen Wert des Mittelwerts der Grundgesamtheit. Für ein gegebenes Signifikanzniveau  zeigt dieses Intervall an, dass wir zeigt dieses Intervall an, dass wir 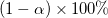 Konfidenz haben, um sagen zu können, dass der wahre Mittelwert der Grundgesamtheit in dem Intervall liegt. Konfidenz haben, um sagen zu können, dass der wahre Mittelwert der Grundgesamtheit in dem Intervall liegt.
Umgang mit fehlenden Werten
Die fehlenden Werte in dem Datenbereich werden aus der Analyse ausgeschlossen.
t-Test bei einer Stichprobe durchführen
Um einen t-Test bei einer Stichprobe durchzuführen:
- Wählen Sie Statistik: Hypothesentests: t-Test bei einer Stichprobe. Der Dialog OneSampletTest wird geöffnet.
- Legen Sie Ihre Eingabedaten, den Testmittelwert und die gewünschte Alternativhypothese fest.
- Indem Sie auf OK klicken, wird ein Berichtsblatt erstellt, das die Freiheitsgrade, die t-Statistik, den zugehörigen p-Wert und die Testschlussfolgerung anzeigt. Zusätzlich können Sie Konfidenzintervalle für den Stichprobenmittelwert, ein Histogramm und ein Boxdiagramm erstellen. Auch eine Analyse der Trennschärfe kann durchgeführt werden. Sie berechnet die Wahrscheinlichkeit, die Nullhypothese zu verwerfen, wenn die Alternativhypothese bei gegebenem Stichprobenumfang wahr ist.
|
Themen, die in diesem Abschnitt behandelt werden:
|
|