Algorithmus (Diskriminanzanalyse)
Die Diskriminanzanalyse wird verwendet, um Beobachtungen Gruppen zuzuweisen. Hierfür werden Informationen über Beobachtungen, deren Gruppenzugehörigkeit bekannt ist, verwendet, d.h. Schulungsdaten.
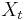 seien die Schulungsdaten mit n Beobachtungen und p Variablen bei ng Gruppen. seien die Schulungsdaten mit n Beobachtungen und p Variablen bei ng Gruppen. 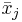 ist ein Zeilenvektor des Stichprobenmittelwerts für die j-te Gruppe, ist ein Zeilenvektor des Stichprobenmittelwerts für die j-te Gruppe, 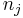 ist die Anzahl der Beobachtungen für die j-te Gruppe. Die Kovarianzmatrix innerhalb der Gruppe für Gruppe j kann ausgedrückt werden durch: ist die Anzahl der Beobachtungen für die j-te Gruppe. Die Kovarianzmatrix innerhalb der Gruppe für Gruppe j kann ausgedrückt werden durch:
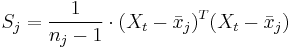
Die gepoolte Kovarianzmatrix innerhalb der Gruppe ist:
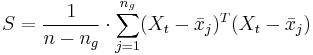
Beachten Sie, dass fehlende Werte listenweise aus der Analyse ausgeschlossen werden, d.h., eine Beobachtung, die einen oder mehrere fehlende Werte enthält, wird aus der Analyse ausgeschlossen.
Gleichheitstest von Kovarianzmatrizen innerhalb von Gruppen
Wenn angenommen wird, dass die Schulungsdaten einer multivariaten Normalverteilung folgen, kann die folgende Statistik des Likelihood-Verhältnis-Tests G verwendet werden, um auf Gleichheit der Kovarianzmatrizen innerhalb der Gruppe zu testen.
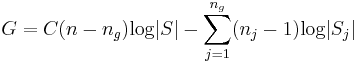
wobei
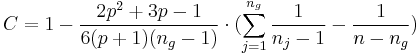
Für große n ist G ungefähr als eine 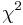 Variable mit Variable mit  Freiheitsgeraden verteilt. Freiheitsgeraden verteilt.
Kanonische Diskriminanzanalyse
Die kanonische Diskriminanzanalyse wird verwendet, um die lineare Kombination der p Variablen zu suchen, die das Verhältnis der Streuung von "zwischen Gruppen" und "innerhalb der Gruppe" maximiert. Die gebildeten kanonischen Variate können dann verwendet werden, um zwischen Gruppen zu unterscheiden.
Die Schulungsdaten mit subtrahierten Gesamtmittelwerten sei X und der Rang sei k, dann kann die orthogonale Matrix Q aus der QR Zerlegung (voller Spaltenrang) oder SVD aus X berechnet werden. 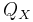 ist die erste k Spalte von Q. ist die erste k Spalte von Q. 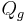 sei eine orthogonale n x ng - 1-Matrix zum Definieren von Gruppen. Dann sei k mal sei eine orthogonale n x ng - 1-Matrix zum Definieren von Gruppen. Dann sei k mal  Matrix V Matrix V
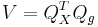
Die SVD von V ist:

Diagonale Elemente (nicht Null) der Matrix  sind die l kanonischen Korrelationen verbunden mit den l kanonischen Variaten sind die l kanonischen Korrelationen verbunden mit den l kanonischen Variaten  i=1,2,...,l und i=1,2,...,l und 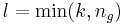 . .
Eigenwerte der Matrix zu den Summen der Quadrate innerhalb der Gruppen sind:

-
- Testen auf eine signifikante Dimensionalität größer als i:

-
- Eine
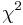 Statistik mit Statistik mit  Freiheitsgraden wird verwendet: Freiheitsgraden wird verwendet:
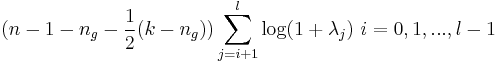
- Nicht standardisierte kanonische Koeffizienten
-
-
Das Laden von Matrix B für kanonische Variate kann berechnet werden aus
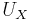 . Dies ist skaliert, so dass die kanonischen Variate eine einheitliche gepoolte Varianz innerhalb der Gruppen haben, d.h. . Dies ist skaliert, so dass die kanonischen Variate eine einheitliche gepoolte Varianz innerhalb der Gruppen haben, d.h.
-
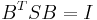
- Beachten Sie, dass das Vorzeichen des Eigenwerts in dem Ergebnis der SVD nicht einzigartig ist, das heißt, jede Spalte B kann mit -1 multipliziert werden. Origin normiert seine Vorzeichen, indem die Summe jeder Spalte in
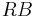 positiv gemacht wird, wobei R die Cholesky-Faktorisierung von S ist. positiv gemacht wird, wobei R die Cholesky-Faktorisierung von S ist.
-
Konstante Elemente können wie folgt berechnet werden:
-
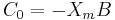
- wobei
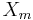 ein Zeilenvektor der Mittelwerte für Variablen ist. ein Zeilenvektor der Mittelwerte für Variablen ist.
- Standardisierte kanonische Koeffizienten
-
-
-
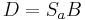
- wobei
 eine diagonale Matrix ist, deren diagonale Elemente die Quadratwurzeln der diagonalen Elemente der gepoolten Gruppenvarianzmatrix S innerhalb der Gruppen sind eine diagonale Matrix ist, deren diagonale Elemente die Quadratwurzeln der diagonalen Elemente der gepoolten Gruppenvarianzmatrix S innerhalb der Gruppen sind
- Kanonische Strukturmatrix
-
-
-
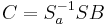
- Kanonische Gruppenmittelwerte
-
-
-
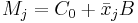
- wobei
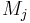 und und 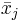 Zeilenvektoren des kanonischen Gruppenmittelwerts bzw. des Gruppenmittelwerts für die j-te Gruppe sind. Zeilenvektoren des kanonischen Gruppenmittelwerts bzw. des Gruppenmittelwerts für die j-te Gruppe sind.
-
-
-
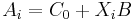
- wobei
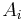 der kanonische Score für die i-te Beobachtung der kanonische Score für die i-te Beobachtung 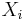 sind. sind.
- Beachten Sie, dass hier die i-te Beobachtung Schulungsdaten oder Testdaten sein können.
Mahalanobis-Distanz
Die Mahalanobis-Distanz ist ein Maß der Distanz einer Beobachtung von einer Gruppe. Sie hat zwei Formen. Für eine Beobachtung 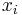 aus der j-ten Gruppe ist die Distanz: aus der j-ten Gruppe ist die Distanz:
- Mit Hilfe der Kovarianzmatrix innerhalb der Gruppe
-
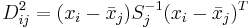
- Mit Hilfe der gepoolten Kovarianzmatrix innerhalb der Gruppen
-
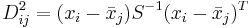
Klassifizieren
A-priori-Zugehörigkeitswahrscheinlichkeit
Die A-priori-Zugehörigkeitswahrscheinlichkeit gibt die Ansicht des Anwenders wieder hinsichtlich der Wahrscheinlichkeit, dass die Beobachtungen aus unterschiedlichen Gruppen stammen. Origin unterstützt zwei Arten von A-priori-Zugehörigkeitswahrscheinlichkeiten:
-
-
-
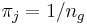
- Proportional zur Gruppengröße
-
-
-
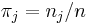
- wobei
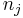 die Anzahl der Beobachtungen in der j-ten Gruppe der Schulungsdaten darstellt. die Anzahl der Beobachtungen in der j-ten Gruppe der Schulungsdaten darstellt.
A-posteriori-Zugehörigkeitswahrscheinlichkeit
Von den p Variablen der Beobachtungen wird angenommen, dass sie einer multivariaten Normalverteilung mit Mittelwert  und Kovarianzmatrix und Kovarianzmatrix 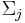 folgen, wenn die Beobachtung aus der j-ten Gruppe stammt. Wenn folgen, wenn die Beobachtung aus der j-ten Gruppe stammt. Wenn  die Wahrscheinlichkeit ist, die Beobachtung die Wahrscheinlichkeit ist, die Beobachtung 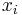 in Gruppe j zu beobachten, dann ist die A-posteriori-Zugehörigkeitswahrscheinlichkeit zur Gruppe j: in Gruppe j zu beobachten, dann ist die A-posteriori-Zugehörigkeitswahrscheinlichkeit zur Gruppe j:
-
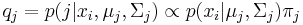
Die Parameter  und und 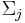 werden in den Schulungsdaten werden in den Schulungsdaten 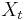 geschätzt. Die Beobachtung wird der Gruppe mit der höhsten A-posteriori-Zugehörigkeitswahrscheinlichkeit zugewiesen. Origin bietet zwei Methoden zum Berechnen der A-posteriori-Zugehörigkeitswahrscheinlichkeit. geschätzt. Die Beobachtung wird der Gruppe mit der höhsten A-posteriori-Zugehörigkeitswahrscheinlichkeit zugewiesen. Origin bietet zwei Methoden zum Berechnen der A-posteriori-Zugehörigkeitswahrscheinlichkeit.
- Lineare Diskriminanzfunktion
-
- Kovarianzmatrizen innerhalb der Gruppe werden als gleich angenommen.
-
-
-
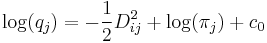
-
- wobei
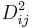 die Mahalanobis-Distanz der i-ten Beobachtung aus der j-ten Gruppe unter Verwendung der gepoolten Kovarianzmatrix innerhalb der Gruppe und die Mahalanobis-Distanz der i-ten Beobachtung aus der j-ten Gruppe unter Verwendung der gepoolten Kovarianzmatrix innerhalb der Gruppe und 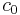 eine Konstante ist. eine Konstante ist.
- Quadratische Diskriminanzfunktion
-
- Kovarianzmatrizen innerhalb der Gruppe werden nicht als gleich angenommen.
-
-
-
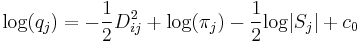
-
- wobei
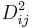 die Mahalanobis-Distanz der i-ten Beobachtung aus der j-ten Gruppe unter Verwendung der Kovarianzmatrizen innerhalb der Gruppe und die Mahalanobis-Distanz der i-ten Beobachtung aus der j-ten Gruppe unter Verwendung der Kovarianzmatrizen innerhalb der Gruppe und  eine Konstante ist. eine Konstante ist.
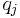 sind folgendermaßen standardisiert und sind folgendermaßen standardisiert und 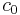 wird durch die Standardisierung bestimmt. wird durch die Standardisierung bestimmt.
-
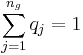
Typikalitätsindex
Der Typikalitätsindex 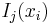 gibt die Wahrscheinlichkeit an, mit der Sie eine Beobachtung erhalten, die typischer für Gruppe j ist als die i-te Beobachtung. Wenn sie für alle Gruppen nah bei 1 liegen, ist das ein Hinweis darauf, dass die Beobachtung von einer Gruppierung stammen könnte, die nicht in den Schulungsdaten dargestellt ist. Der Typikalitätsindex wird berechnet mit: gibt die Wahrscheinlichkeit an, mit der Sie eine Beobachtung erhalten, die typischer für Gruppe j ist als die i-te Beobachtung. Wenn sie für alle Gruppen nah bei 1 liegen, ist das ein Hinweis darauf, dass die Beobachtung von einer Gruppierung stammen könnte, die nicht in den Schulungsdaten dargestellt ist. Der Typikalitätsindex wird berechnet mit:
-
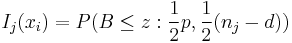
wobei  die untere Wahrscheinlichkeit aus einer Beta-Verteilung für gleiche Kovarianzmatrizen innerhalb von Gruppen is, die untere Wahrscheinlichkeit aus einer Beta-Verteilung für gleiche Kovarianzmatrizen innerhalb von Gruppen is,
-
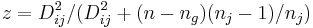
für nicht gleiche Kovarianzmatrizen innerhalb der Gruppe,
-
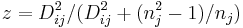
Lineare Koeffizienten der Diskriminanzfunktion
Die lineare Diskriminanzfunktion (auch bekannt als Fishers lineare Diskriminanzfunktionen) kann berechnet werden mit:
- Linearer Koeffizient für die j-te Gruppe:
-
-
-

- wobei
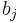 ein Spaltenvektor mit der Größe von p ist. ein Spaltenvektor mit der Größe von p ist.
- Konstanter Koeffizient für die j-te Gruppe:
-
-
-
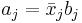
Schulungsdaten klassifizieren
Jede Beobachtung in den Schulungsdaten kann durch A-posteriori-Zugehörigkeitswahrscheinlichkeiten klassifiziert werden, d.h., sie wird der Gruppe mit der höchsten A-posteriori-Zugehörigkeitswahrscheinlichkeit zugeordnet. Die quadrierte Mahalanobis-Distanz von jeder Gruppe und der Typikalitätsindex von jeder Gruppe können ebenfalls berechnet werden.
Das Klassifizierungsergebnis für Schulungsdaten wird zusammengefasst, indem gegebene Gruppenzugehörigkeit und vorhergesagte Gruppenzugehörigkeit verglichen werden. Eine fehlklassifizierte Fehlerrate wird durch den Prozentsatz der fehlklassifizierten Beobachtungen berechnet, gewichtet durch die A-priori-Zugehörigkeitswahrscheinlichkeiten der Gruppen. d.h.
-
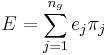
wobei 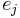 der Prozentsatz der fehlklassifizierten Beobachtungen für die j-te Gruppe ist. der Prozentsatz der fehlklassifizierten Beobachtungen für die j-te Gruppe ist.
Kreuzvalidierung für Schulungsdaten
Es erfolgt der gleiche Vorgang wie beim Klassifizieren der Schulungsdaten, nur dass, um eine Beobachtungszugehörigkeit in den Schulungsdaten vorhersagen zu können, die Beobachtung während der Berechnung der Kovarianzmatrizen innerhalb der Gruppe oder der gepoolten Kovarianzmatrix innerhalb der Gruppe ausgeschlossen ist.
Testdaten klassifizieren
Kovarianzmatrizen innerhalb der Gruppe und die gepoolte Kovarianzmatrix innerhalb der Gruppe werden aus den Schulungsdaten berechnet. Jede Beobachtung in den Testdaten kann durch A-posteriori-Zugehörigkeitswahrscheinlichkeiten klassifiziert werden, d.h., sie wird der Gruppe mit der höchsten A-posteriori-Zugehörigkeitswahrscheinlichkeit zugeordnet.
|