Algorithmus (sign2)
Der Vorzeichentest bei verbundenen Stichproben testet die Mediandifferenz zwischen Wertepaaren aus zwei einander entsprechenden Stichproben.
Für zwei einander entsprechende Stichproben 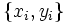 , , 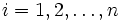 ist die Nullhypothese ist die Nullhypothese 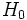 , dass die Mediane der verbundenen Stichproben gleich sind, während die Alternativhypothese , dass die Mediane der verbundenen Stichproben gleich sind, während die Alternativhypothese 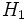 ein- oder beidseitig sein kann (siehe unten). Es wird berechnet: ein- oder beidseitig sein kann (siehe unten). Es wird berechnet:
- Die Teststatistik
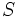 , die die Anzahl der Paare darstellt, bei denen , die die Anzahl der Paare darstellt, bei denen 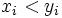 ; ;
- Die Anzahl
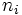 der nicht verbundenen Paare ( der nicht verbundenen Paare (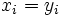 ); );
- Die untere Wahrscheinlichkeit
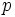 , die , die 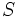 entspricht (angepasst, um das Komplement entspricht (angepasst, um das Komplement 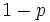 in einem oberen oder beidseitigen Test zu verwenden). in einem oberen oder beidseitigen Test zu verwenden). 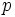 ist die Wahrscheinlichkeit, einen Wert ist die Wahrscheinlichkeit, einen Wert 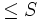 zu beobachten, wenn zu beobachten, wenn 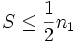 ; oder einen Wert ; oder einen Wert 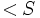 zu beobachten, wenn zu beobachten, wenn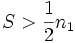 , vorausgesetzt, dass , vorausgesetzt, dass 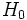 wahr ist. Wenn wahr ist. Wenn 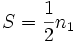 , dann ist , dann ist 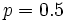 . .
Angenommen, der Signifikanztest einer gewählten Größe 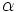 soll durchgeführt werden (d.h., soll durchgeführt werden (d.h., 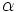 ist die Wahrscheinlichkeit, ist die Wahrscheinlichkeit, 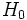 zurückzuweisen, wenn zurückzuweisen, wenn 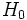 wahr ist; normalerweise ist wahr ist; normalerweise ist 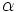 ein kleiner Betrag wie 0,05 oder 0,01). Der zurückgegebene Wert von ein kleiner Betrag wie 0,05 oder 0,01). Der zurückgegebene Wert von 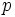 kann verwendet werden, um den Signifikanztest für die Mediandifferenz gegen verschiedene Alternativhypothesen kann verwendet werden, um den Signifikanztest für die Mediandifferenz gegen verschiedene Alternativhypothesen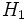 durchzuführen, wie folgt: durchzuführen, wie folgt:
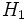 : Median von : Median von 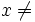 Median von Median von 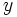 . . 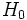 wird zurückgewiesen, wenn wird zurückgewiesen, wenn 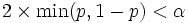 . .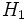 : Median von : Median von 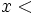 Median von Median von 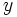 . . 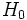 wird zurückgewiesen, wenn wird zurückgewiesen, wenn 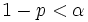 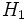 : Median von : Median von 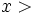 Median von Median von 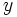 . . 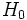 wird zurückgewiesen, wenn wird zurückgewiesen, wenn 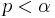
Weitere Einzelheiten zu dem Algorithmus finden Sie unter nag_sign_test (g08aac).
|