2D-Interpolation/Extrapolation
Math-2D-Inter-Extrapolate
Übersicht
Mit der 2D-Interpolation/-Extrapolation können Sie entweder eine Gruppe von existierenden XYZ-Daten für einen gegebenen XY-Datensatz oder ein festgelegtes Matrixobjekt interpolieren/extrapolieren.
Aus XY interpolieren
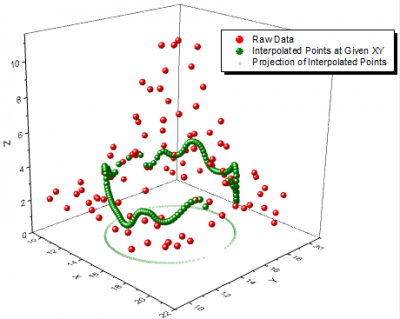
Das Hilfsmittel Z aus XY interpolieren erlaubt Ihnen, einen Satz von XY-Werten für die Interpolation/Extrapolation festzulegen, so dass zusätzliche Freiheit bei der 2D-Interpolation/-Extrapolation für nicht-äquidistant verteilte XY-Datensätze entsteht. Origin unterstützt 8 Interpolationsmethoden zum Interpolieren von Z aus XY: Nächster Nachbar, Random Kriging, Random Renka-Kline, Random Shepard, Random TPS, Spline, Dreieck, Gewichtetes Mittel.
Z aus XY interpolieren
- Aktivieren Sie die Arbeitsmappe, die die Eingabedaten enthält.
- Wählen Sie Analyse: Mathematik: Z aus XY interpolieren im Menü. Der Dialog interp2 wird geöffnet.
- Wählen Sie Ihre Eingabeoptionen und klicken Sie auf OK. Die X-Funktion interp2 wird aufgerufen, um die Berechnung durchzuführen.
Dialogoptionen für Z aus XY interpolieren
Lesen Sie in der Dokumentation der X-Funktion interp2 Einzelheiten zu den Dialogbedienelemente des Hilfsmittels Z aus XY interpolieren.
2D-Interpolation für Matrix
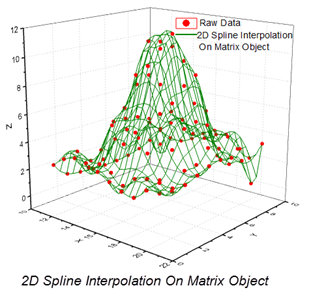
Die zweidimensionale Interpolation/Extrapolation kann für Daten durchgeführt werden, die in einer Origin-Matrix gespeichert sind. Origin unterstützt fünf Methoden für die Interpolation einer Matrix: Nächster Nachbar, Bilinear, Bikubisch, Spline, Biquadratisch. Sie können auch die Ausgabebereiche der Interpolation für X und Y festlegen.
2D-Interpolation für Matrix durchführen
- Aktivieren Sie die Matrix, die die Eingabedaten enthält.
- Wählen Sie Analyse: Mathematik: 2D-Interpolation/Extrapolation im Origin-Menü. Der Dialog minterp2 wird geöffnet.
- Wählen Sie Ihre Eingabeoptionen und klicken Sie auf OK. Die X-Funktion minterp2 wird aufgerufen, um die Berechnung abzuschließen.
Dialogoptionen für 2D-Interpolation für Matrix
| Neu berechnen |
Bedienelemente zur Neuberechnung der Analyseergebnisse
Weitere Informationen finden Sie unter Analyseergebnisse neu berechnen.
|
| Eingabematrix |
Legt die Matrix fest, die die zu interpolierenden/extrapolierenden Daten enthält.
Hilfe zum Festlegen von Bereichen finden Sie hier: Eingabedaten festlegen
|
| Methode |
Legt die Interpolations-/Extrapolationsmethode fest.
-
Nächster
- Mit Hilfe der am nächsten liegenden Punkten interpolieren
-
Bilinear
- Zweidimensionale lineare Interpolation
-
Bikubische Faltung
- Zweidimensionale Interpolation mit der bikubischen Faltung
-
Spline
- Zweidimensionale Spline-Interpolation
-
Biquadratisch
- Zweidimensionale quadratische Interpolation
-
Bikubische Lagrange
- Zweidimensionale Interpolation mit Langrange-Polynomen
|
| Anzahl der Spalten |
Legt die Spaltenanzahl der Ausgabematrix fest.
|
| Anzahl der Zeilen |
Legt die Zeilenanzahl der Ausgabematrix fest.
|
| Vorbehandlung von fehlenden Werten |
Legt die Methode fest, um fehlende Werte in der 2D-Interpolation vorzuverarbeiten.
-
Überspringen
- Alle fehlenden Werte werden zuerst entfernt und dann eine wird eine Interpolation ausgeführt.
-
Interpoliert mit Renka Cline
- Renka Cline: Berechnet für einen beliebigen Punkt P den interpolierten Wert mit Hilfe der Datenwerte und der geschätzten Gradienten an jedem der drei Eckpunkte des Dreiecks, das P enthält.
|
| Koordinaten |
Legt die Koordinaten/XY-Abbildung der Ausgabematrix fest.
-
Erstes X
- Der letzte X-Wert der Ausgabematrix
-
Letztes X
- Der letzte X-Wert der Ausgabematrix
-
Erstes Y
- Der erste Y-Wert der Ausgabematrix
-
Letztes Y
- Der letzte Y-Wert der Ausgabematrix
|
| Ausgabematrix |
Legt die Ausgabematrix für die interpolierten/extrapolierten Daten fest.
|
Algorithmus für Interpolation für Matrix
Interpolation des nächsten Nachbarn:
Berechnet den interpolierten Wert mit Hilfe der am nächsten liegenden Gitterpunkte.
Polynomiale Interpolation:
Dieser Typ der Interpolation umfasst die Methoden Bilinear, Biquadratisch und Bikubische Faltung und Bikubische Lagrange, von denen alle ähnlich vorgehen. Beispielsweise können Sie, um den Wert bei 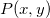 mit der biquadratischen Interpolationsmethode zu berechnen, zuerst die quadratische 1D-Interpolation vertikal durchführen, basierend auf den Datenpunkten mit der biquadratischen Interpolationsmethode zu berechnen, zuerst die quadratische 1D-Interpolation vertikal durchführen, basierend auf den Datenpunkten 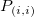 , , 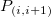 , , 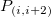 , um , um 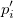 zu erzeugen, das den gleichen zu erzeugen, das den gleichen 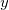 -Wert hat wie -Wert hat wie 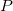 . Dann berechnen Sie . Dann berechnen Sie 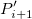 und und 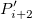 . Die Werte . Die Werte 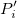 , , 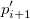 und und 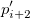 definieren eine Linie durch definieren eine Linie durch 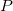 . Danach führen Sie die quadratische 1D-Interpolation horizontal durch, um den Wert bei . Danach führen Sie die quadratische 1D-Interpolation horizontal durch, um den Wert bei 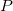 auszuwerten. auszuwerten.
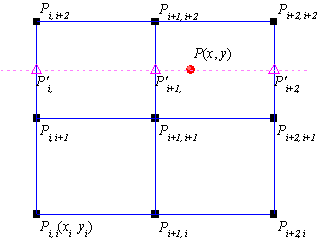
Der Unterschied zwischen den Methoden Bilinear, Biquadratisch, Bikubische Faltung und Bikubische Lagrange ist, dass sie unterschiedliche Ordnungen der Polynomfunktionen verwenden. Das interpolierende Polynom der Ordnung n-1 durch n Punkte ist:
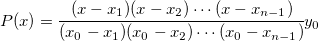 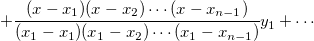 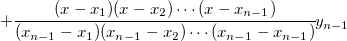
Spline-Interpolation:
Diese Methode berechnet Werte der bikubischen Spline 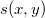 durch: durch:
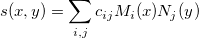
wobei 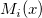 und und 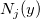 die normierten kubischen B-Splines bezeichnen und die normierten kubischen B-Splines bezeichnen und 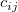 der Spline-Koeffizient ist. der Spline-Koeffizient ist.
Weitere Informationen zur 2D-Spline-Interpolation finden Sie in der Dokumentation zur NAG-Funktion e02dec.
Referenzen
- Willian H. Press, etc. Numerical Recipes in C++, 2nd Edition. Cambridge University Press (2002)
|