Schnelle Fourier-Transformation (FFT)
Eine diskrete Fourier-Transformation (DFT) konvertiert ein Signal im Zeitbereich
in seine Gegenstücke im Frequenzbereich. Angenommen (
xi) ist eine Sequenz
der Länge N, dann ist die DFT die Sequenz (
Fn) gegeben durch
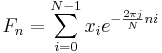
Eine schnelle Fourier-Transformation (FFT) ist eine effektive Methode
zum Berechnen der DFT. Wird die FFT anstatt der DFT verwendet, kann die
Berechnungskomplexität von O(n2)
auf O(n log n) verringert werden. Beachten Sie, dass das Eingabesignal
von FFT in Origin komplex und von beliebiger Größe sein kann.
Das Ergebnis von FFT enthält die Frequenzdaten und das komplexe transformierte
Ergebnis. Außerdem kann es auch Betrag, Amplitude, Phase, Leistungsdichte
und andere Berechnungsergebnisse bieten. Die Schätzung der Leistungsdichte
kann mit drei verschiedenen Methoden durchgeführt werden: MSA, SSA und
TISA. Zudem können zweiseitige und einseitige Leistungsspektren berechnet
werden.
Wenn die FFT verwendet wird, sollten die Verluste beachtet werden, die
von der Annahme der FFT verursacht werden, dass das Eingabesignal periodisch
wiederholt wird und die periodische Länge gleich der Länge der tatsächlichen
Eingabe ist. Wenn das wahre Signal jedoch nicht periodisch ist
oder die angenommene periodische Länge nicht korrekt ist, treten
Verluste auf. Dadurch werden die Amplitude und die Position einer Frequenzmessung
ungenau. Origin unterstützt die Verwendung der Fensterfunktionen, um den
Verlust abzuschwächen. Mehrere Fensterfunktionen werden unterstützt, einschließlich
Triangular, Bartlett, Welch, Hanning, Hamming und Blackman, die jeweils
ganz eigene Vor- und Nachteile haben. Eine spezifische Fensterfunktion
sollte gemäß der Art des zu analysierenden Signals ausgewählt werden.
Um die
FFT zu verwenden:
- Aktivieren Sie eine Arbeitsmappe oder ein Diagramm.
- Wählen Sie Analyse: Signalverarbeitung: FFT: FFT im Origin-Menü.
|